Файл: Задача 1 Расчет нелинейной электрической цепи переменного тока.docx
Добавлен: 26.10.2023
Просмотров: 33
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
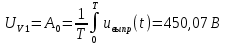 (11)
(11)Вольтметр PV2 является измерительным прибором электромагнитной системы, который реагирует на действующее значение несинусоидального выходного напряжения полупроводникового выпрямителя uвыпр(t). Действующее значение несинусоидального напряжения найдем следующим образом (формула 12).
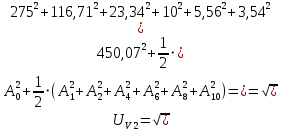
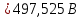 (12)
(12)где A0 – постоянная составляющая или нулевая гармоника, Ak – амплитуды k – гармонических составляющих ряда Фурье. Вольтметр PV3 является измерительным прибором выпрямительной системы, который реагирует на среднее значение по модулю несинусоидального выходного напряжения полупроводникового выпрямителя uвыпр(t). Основой данного измерительного прибора является вольтметр магнитоэлектрической системы, в который встроен полупроводниковый выпрямительный мост. Мостовой выпрямитель выполняется математическую функцию модуля функции, следовательно, среднее значение несинусоидального напряжения найдем следующим образом (формула 13). Занесем расчетные показания напряжений вольтметров в таблицу 3.
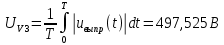 (13)
(13)Таблица 3 – Сводная таблица показаний вольтметра.
| Показания приборов | Расчетные данные |
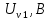 | 450,07 |
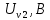 | 497,525 |
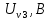 | 497,525 |
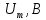 | 481,707 |
Определим коэффициент искажения несинусоидального напряжения uвыпр(t), который равен отношению действующего значения первой гармоники к действующему значению несинусоидального напряжения (формула 14).
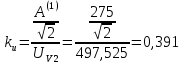 (14)
(14)Данный коэффициент показывает, насколько близка несинусоидальная функция к синусоидальному закону изменения.
Пункт 4
Рассмотрим, как проходит сигнал через разные реактивные цепи. В качестве реактивного элемента, возьмем индуктивность L (рисунок 8). Электрическая цепь R-L является частотно-зависимым делителем напряжения и выходной сигнал полупроводникового выпрямителя при прохождении через данную цепь изменит свою форму. Найдем характер этого изменения расчетным путем.
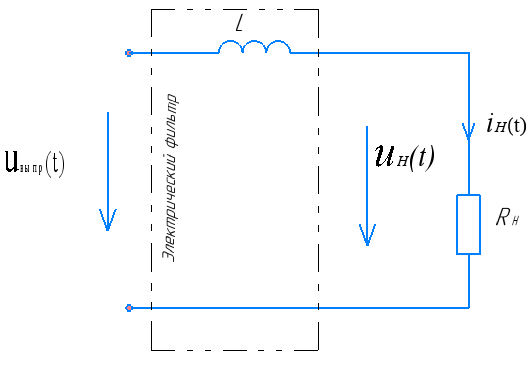
Рисунок 8 – Расчетная электрическая цепь в пункте 4
Основываясь на принципе наложения, справедливым для линейных электрических цепей, расчет цепей при воздействии несинусоидальных напряжений проводится для каждой гармонической составляющей в отдельности, а потом результаты суммируются. Для этого представим каждую гармоническую составляющую несинусоидального напряжения 22 полупроводникового выпрямителя uвыпр(t) комплексной амплитудой. Результаты этой записи представлены в таблице 4.

Таблица 4 – Комплексные амплитуды гармоник напряжения
| k | Параметры гармоник | Комплексная амплитуда напряжения | ||
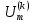 | 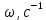 | | 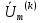 ,B ,B | |
| 0 | 450,07 | 0 | - | 450,07 |
| 1 | 275 | 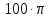 | 1,571 | 275i |
| 2 | 116,71 | 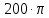 | 1,571 | 116,714i |
| 3 | 0 | 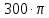 | 1,43 | 0 |
| 4 | 23,34 | 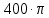 | 4,712 | -23,343i |
| 5 | 0 | 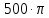 | 2,662 | 0 |
| 6 | 10 | 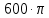 | 1,571 | 10,004i |
| 7 | 0 | 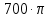 | -0,432 | 0 |
| 8 | 5,56 | 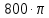 | 4,712 | -5,558i |
| 9 | 0 | 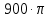 | 1,168 | 0 |
| 10 | 3,54 | 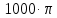 | 1,571 | 3,537i |
Произвольно зададимся параметрами L – фильтра и сопротивлением нагрузки RН. Пусть RН 24 Ом, а L 0,34 Гн, тогда комплексное сопротивление цепи определится следующим образом (формула 15).
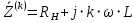 (15)
(15)Занесём значения комплексных сопротивлений от номера гармоники в таблицу 6. Определим комплексные амплитуды гармоник тока, протекающего в цепи по закону Ома (формула 16).
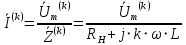 (16)
(16)Комплексные амплитуды гармоник напряжения в нагрузке определим следующим образом (формула 17):
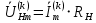 (17)
(17)Результаты всех расчетов по пункту сведем в таблицу 5.
Таблица 5 – Расчетные комплексные величины L – фильтра
| k | Параметры цепи | Комплексная амплитуда напряжения | ||
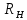 ,Ом ,Ом | 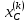 ,Ом ,Ом | 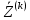 ,Ом ,Ом | 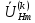 ,B ,B | |
| 0 | 24 | 0 | 24 | 450,07 |
| 1 | 24 | 107 | 24+107j | 58,82+13,216i |
| 2 | 24 | 214 | 24+214j | 12,949+1,455i |
| 3 | 24 | 320 | 24+320j | 0 |
| 4 | 24 | 427 | 24+427j | -1,307-0,073i |
| 5 | 24 | 534 | 24+534j | 0 |
| 6 | 24 | 641 | 24+641j | 0,374+0,014i |
| 7 | 24 | 748 | 24+748j | 0 |
| 8 | 24 | 855 | 24+855j | -0,156-0,004i |
| 9 | 24 | 961 | 24+961j | 0 |
| 10 | 24 | 1068 | 24+1068j | 0,079-0,002i |
Используя данные расчета комплексных амплитуд гармоник напряжения в нагрузке, запишем выражение этого напряжения на временной плоскости с помощью ряда Фурье (формула 18).
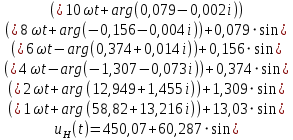 (18)
(18) Воспользуемся встроенной панелью инструментов «График» в математическом пакете Mathcad, построим кривую напряжения нагрузки uH(t) в интервале двух периодов и сравним с кривой напряжения пункта 2.
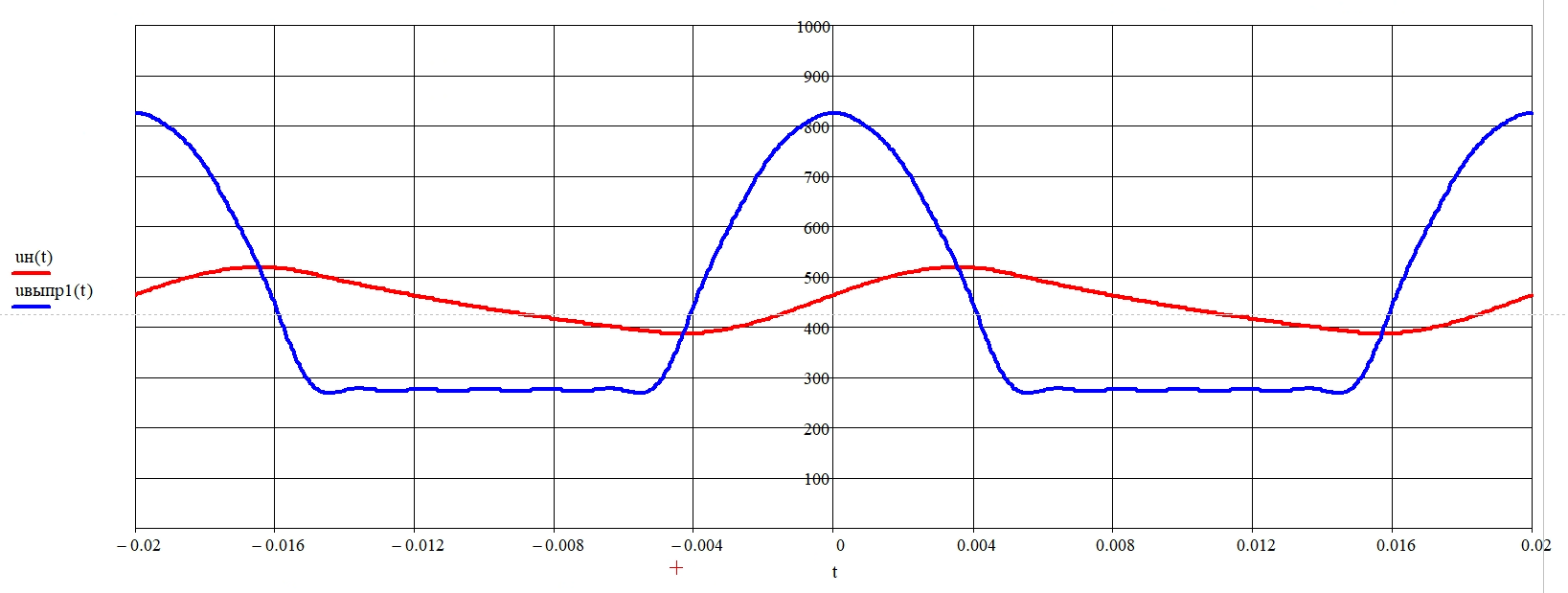
Рисунок 9 – Формы кривых напряжения нагрузки uН (t) и выходного напряжения полупроводникового выпрямителя uвыпр(t)
С помощью встроенной панели инструментов «График» отобразим амплитуды гармонических составляющих ряда Фурье в зависимости от номера гармоники и получим график спектра амплитуд (рисунок 10) напряжения нагрузки.
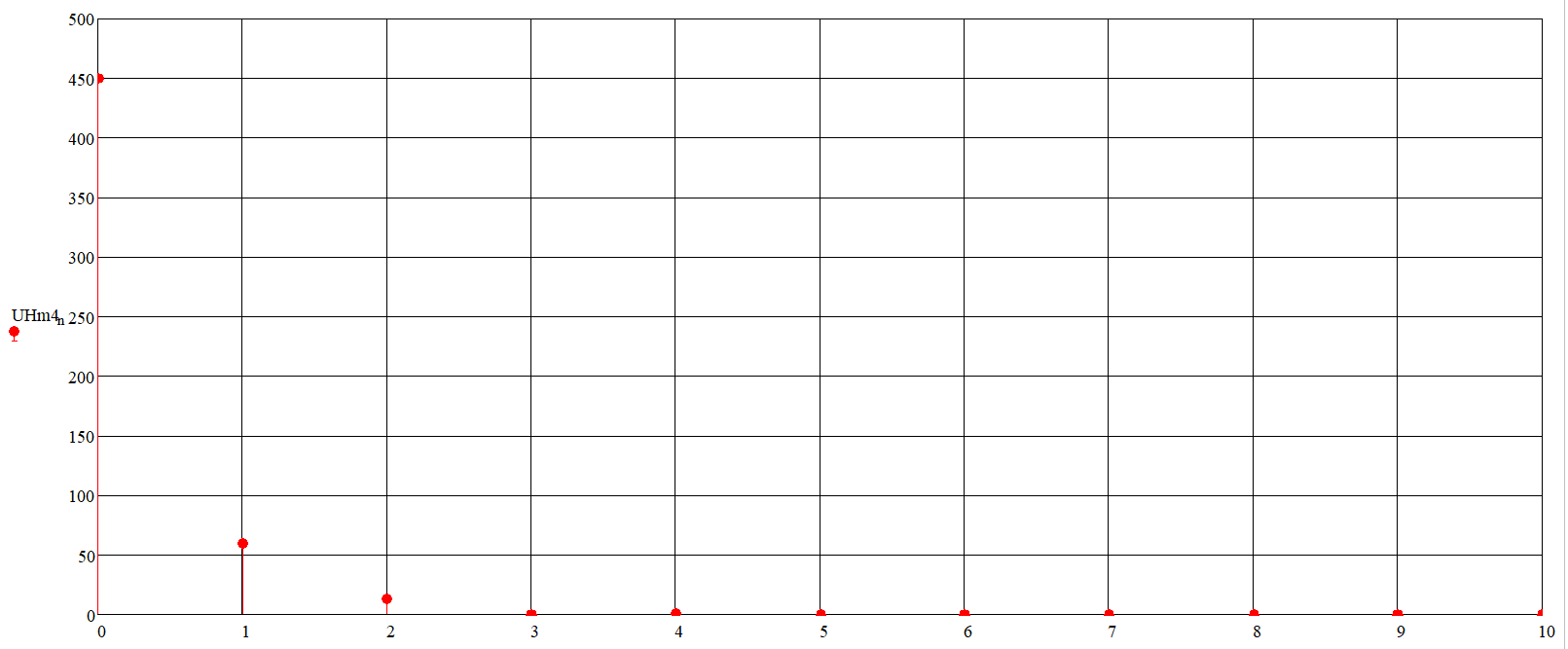
Рисунок 10 – Дискретный спектр амплитуд напряжения нагрузки
Значения начальных фаз гармонических составляющих ряда Фурье отобразим в градусах и получим график спектра фаз (рисунок 11) напряжения нагрузки.
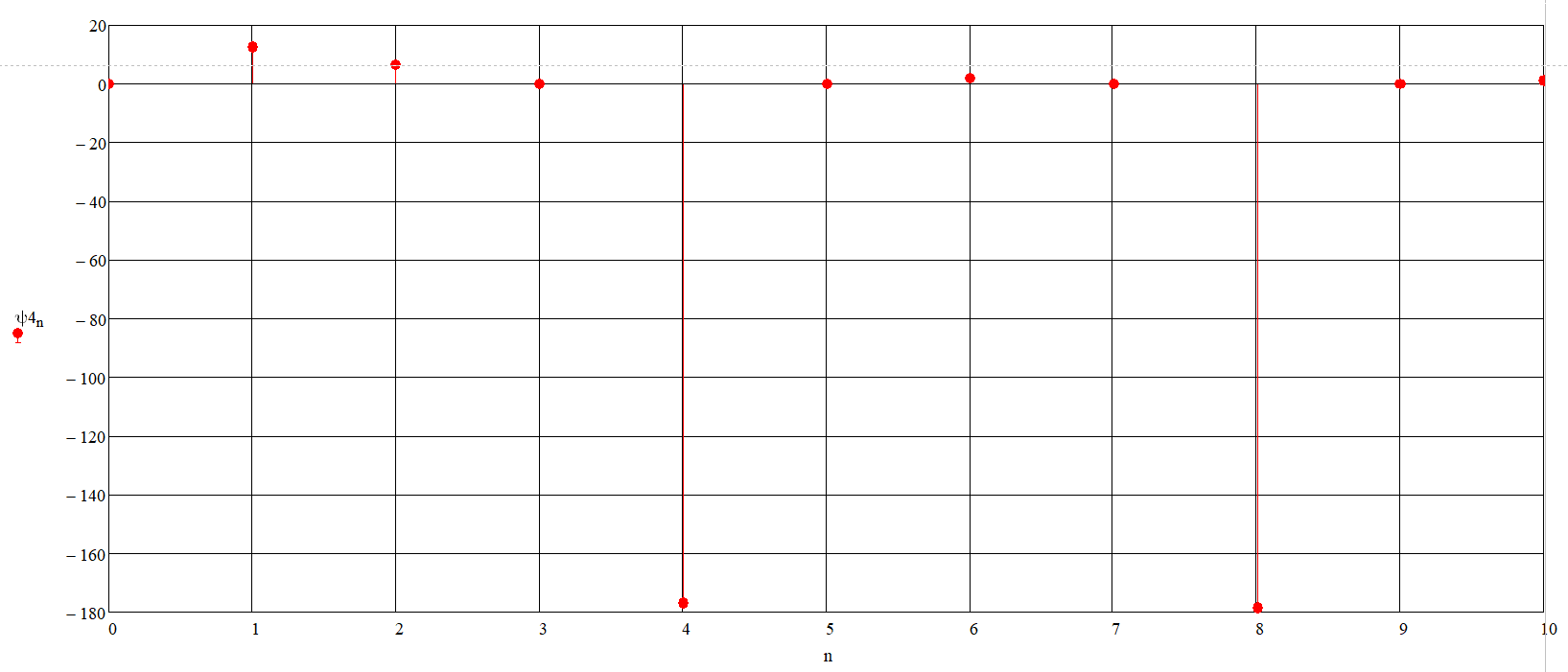
Рисунок 11 – Дискретный спектр фаз напряжения нагрузки
Проведя анализ графика спектра амплитуд, можно сделать вывод, что произошло ослабление амплитуд высших гармоник при прохождении сигнала через индуктивность.
Действующее значение несинусоидального напряжения найдем по (формуле 19).
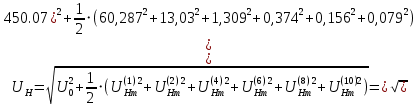
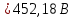 (19)
(19)Определим коэффициент искажения несинусоидального напряжения uН(t), который равен отношению действующего значения первой гармоники к действующему значению несинусоидального напряжения (формула 20).
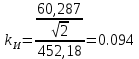 (20)
(20)По расчету видно, что значение коэффициента искажения уменьшилось по сравнению с пунктом 3 Это значит, что форма напряжения нагрузки меньше походит на синусоиду, то есть форма напряжения нагрузки становится более искривленной.
Пункт 5
Рассмотрим, как проходит сигнал через емкостной элемент (рисунок 12). Электрическая цепь R-С также является частотно-зависимым делителем напряжения и выходной сигнал полупроводникового выпрямителя при прохождении через данную цепь изменит свою форму. Найдем характер этого изменения расчетным путем.
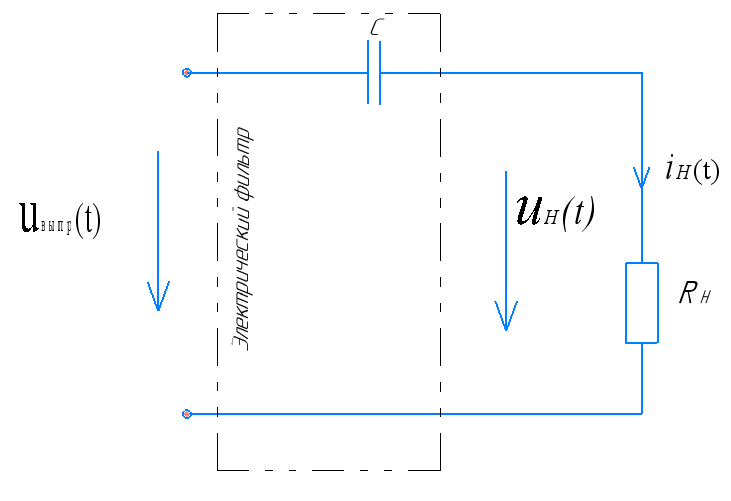
Рисунок 12 – Расчетная электрическая цепь в пункте 5
Источником несинусоидального периодического сигнала является полупроводниковый выпрямитель, поэтому комплексные амплитуды гармоник напряжений будут такие же как в пункте 4 и сведены в таблицу 4. Произвольно зададимся параметрами С – фильтра и сопротивлением нагрузки RН. Пусть RН 24 Ом, а С 22 мкФ, тогда комплексное сопротивление цепи определится следующим образом (формула 21).
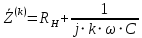 (21)
(21)Занесём значения комплексных сопротивлений от номера гармоники в таблицу 6.
Определим комплексные амплитуды гармоник тока, протекающего в цепи по закону Ома (формула 22):
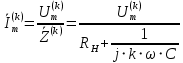 (22)
(22)Комплексные амплитуды гармоник напряжения в нагрузке определим следующим образом (формула 23):
 (23)
(23)Результаты всех расчетов по пункту сведем в таблицу 6.
Таблица 6 – Таблица параметров С-фильтра
| k | Параметры цепи | Комплексная амплитуда напряжения | ||
 ,Ом ,Ом |  ,Ом ,Ом |  ,Ом ,Ом |  ,B ,B | |
| 0 | 24 | 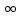 | 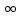 | 0 |
| 1 | 24 | 145 | 24-j145 | -44,394+7,364i |
| 2 | 24 | 72 | 24-j72 | -34,881+11,572i |
| 3 | 24 | 48 | 24-j48 | 0 |
| 4 | 24 | 36 | 24-j36 | 10,754-7,135i |
| 5 | 24 | 29 | 24-j29 | 0 |
| 6 | 24 | 24 | 24-j24 | -5,002+4,978i |
| 7 | 24 | 21 | 24-j21 | 0 |
| 8 | 24 | 18 | 24-j18 | 2,671-3,545i |
| 9 | 24 | 16 | 24-j16 | 0 |
| 10 | 24 | 14 | 24-j14 | -1,564+2,594i |