Файл: Задача 1 Расчет нелинейной электрической цепи переменного тока.docx
Добавлен: 26.10.2023
Просмотров: 34
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Используя данные расчета комплексных амплитуд гармоник напряжения в нагрузке, запишем выражение этого напряжения на временной плоскости с помощью ряда Фурье (формула 24).
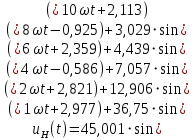 (24)
(24)Воспользуемся встроенной панелью инструментов «График» в математическом пакете Mathcad, построим кривую напряжения нагрузки uн(t) в интервале двух периодов и сравним с кривой напряжения пункта 2 (рисунок 13).
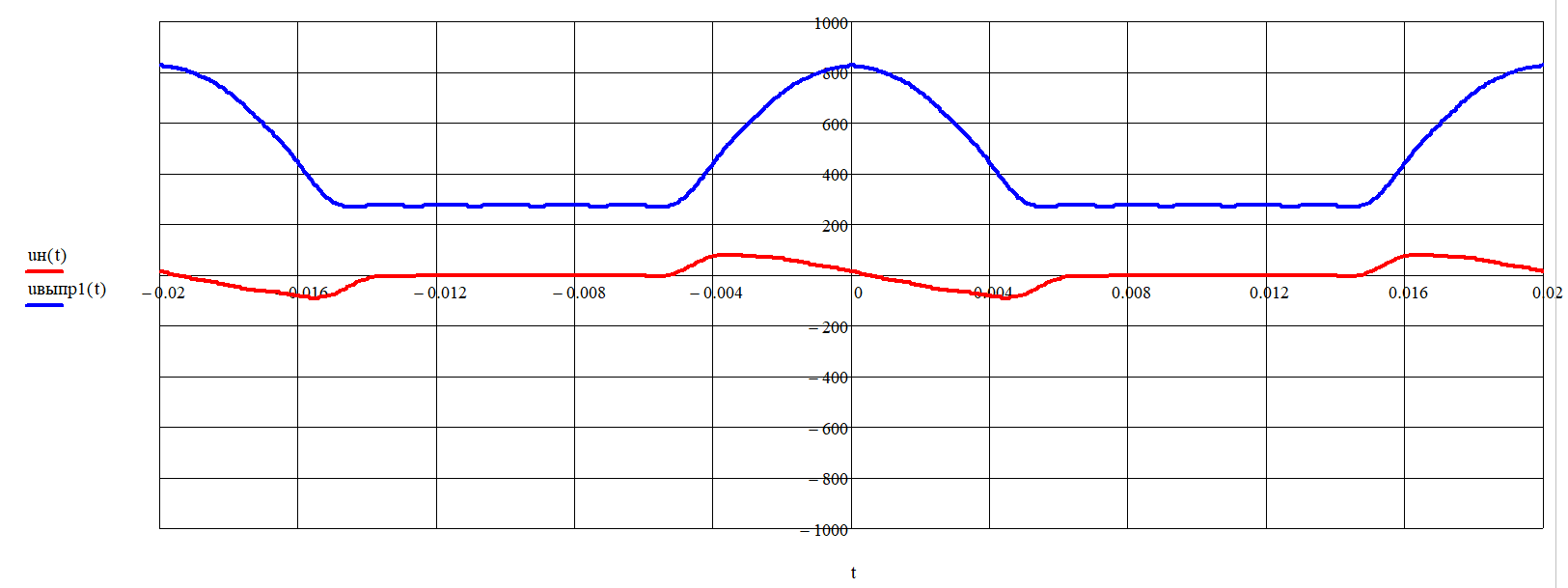
Рисунок 13 – Формы кривых напряжения нагрузки uН(t) и выходного напряжения полупроводникового выпрямителя uвыпр(t)
С помощью встроенной панели инструментов «График» отобразим амплитуды гармонических составляющих ряда Фурье в зависимости от номера гармоники и получим график спектра амплитуд (рис. 14) напряжения нагрузки.
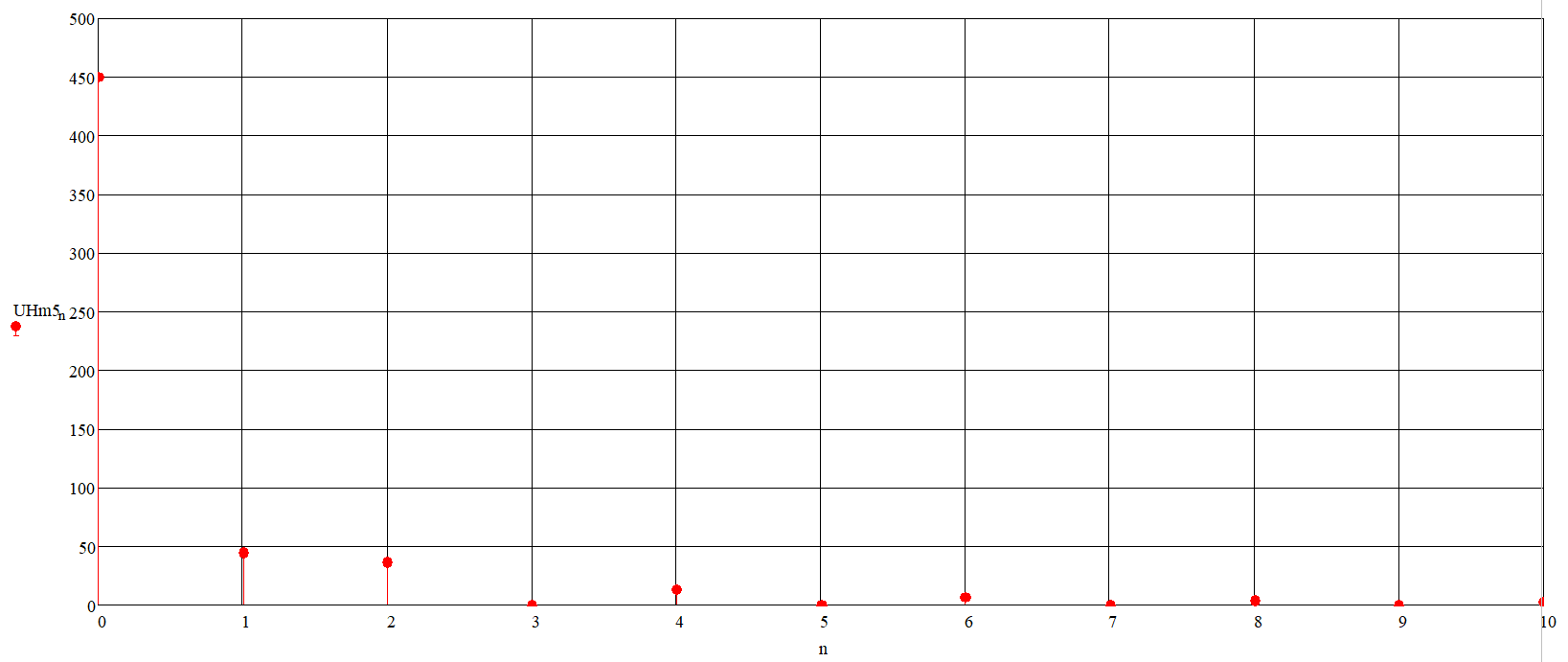
Рисунок 14 – Дискретный спектр амплитуд напряжения нагрузки
Значения начальных фаз гармонических составляющих ряда Фурье отобразим в градусах и получим график спектра фаз (рис. 15) напряжения нагрузки.
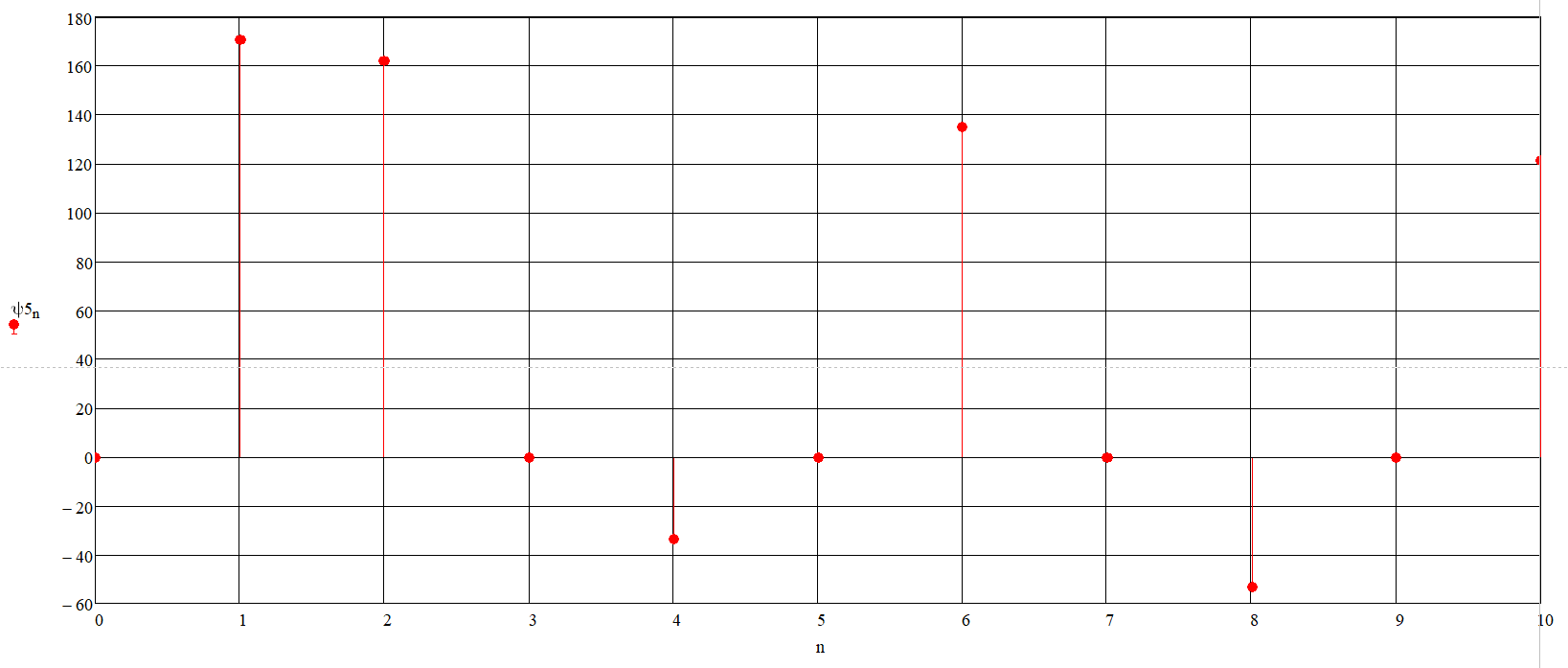
Рисунок 15 – Дискретный спектр фаз напряжения нагрузки
Проведя анализ графика спектра амплитуд, можно сделать вывод, что произошло усиление амплитуд высших гармоник при прохождении сигнала через конденсатор.
Действующее значение несинусоидального напряжения найдем по формуле 25.
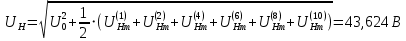 (25)
(25)Определим коэффициент искажения несинусоидального напряжения 26.
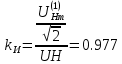 (26)
(26)По расчету видно, что значение коэффициента искажения увеличилось по сравнению с пунктом 3, то есть форма напряжения нагрузки приближается к синусоидальной или форма напряжения нагрузки становится более сглаженной.
Пункт 6
Рассмотрим, как проходит сигнал через заграждающий фильтр (ЗФ) настроенный на нулевую гармонику. Выходной сигнал, проходящий через этот фильтр, должен пройти без нулевой гармоники. Найдем характер этого изменения расчетным путем.
Источником несинусоидального периодического сигнала является полупроводниковый выпрямитель, поэтому комплексные амплитуды гармоник напряжений будут такие же как в пункте 4 и сведены в таблицу 4.
Необходимо рассчитать значения реактивных элементов, то есть настроить L-C-фильтр на данную частоту. Если RН 24 Ом, а L 0,34 Гн, то величина резонансной емкости найдется по формуле 27:
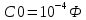 (27)
(27)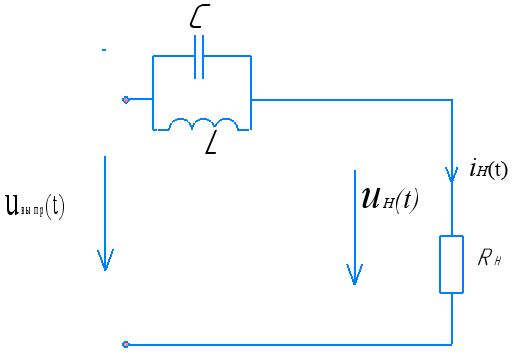
Рисунок 16 – Расчетная электрическая цепь в пункте 6
Комплексное сопротивление цепи определится по формуле 28.
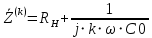 (28)
(28)Занесём значения комплексных сопротивлений от номера гармоники в таблицу 8.
Определим комплексные амплитуды гармоник тока, протекающего в цепи по закону Ома (формула 29).
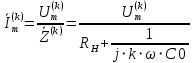 (29)
(29)Комплексные амплитуды гармоник напряжения в нагрузке определим следующим образом (формула 31).
 (31)
(31)Результаты всех расчетов по пункту сведем в таблицу 7
Таблица 7 – Расчетные комплексные величины L-С -фильтра.
| K – номер гармоники | Параметры цепи | Комплексная амплитуда напряжения | |||
 ,Ом ,Ом | 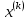 ,Ом ,Ом |  ,Ом ,Ом |  ,B ,B | ||
| 0 | 24 |  |  | 0 | |
| 1 | 24 | -32 | 24-32i | -132,194+99,672i | |
| 2 | 24 | -16 | 24-16i | -53,758+81,065i | |
| 3 | 24 | -11 | 24-11i | 0 | |
| 4 | 24 | -8 | 24-8i | 6,973-21,031i | |
| 5 | 24 | -6 | 24-6i | 0 | |
| 6 | 24 | -5 | 24-5i | -2,108+9,538i | |
| 7 | 24 | -5 | 24-5i | 0 | |
| 8 | 24 | -4 | 24-4i | 0,897-5,409i | |
| 9 | 24 | -4 | 24-4i | 0 | |
| 10 | 24 | -3 | 24-3i | -0,461+3,476i | |
Используя данные расчета комплексных амплитуд гармоник напряжения в нагрузке, запишем выражение этого напряжения на временной плоскости с помощью ряда Фурье (формула 32).

Воспользуемся встроенной панелью инструментов «График» в математическом пакете Mathcad, построим кривую напряжения нагрузки uH(t) в интервале двух периодов и сравним с кривой напряжения пункта 2 (рисунок 17).
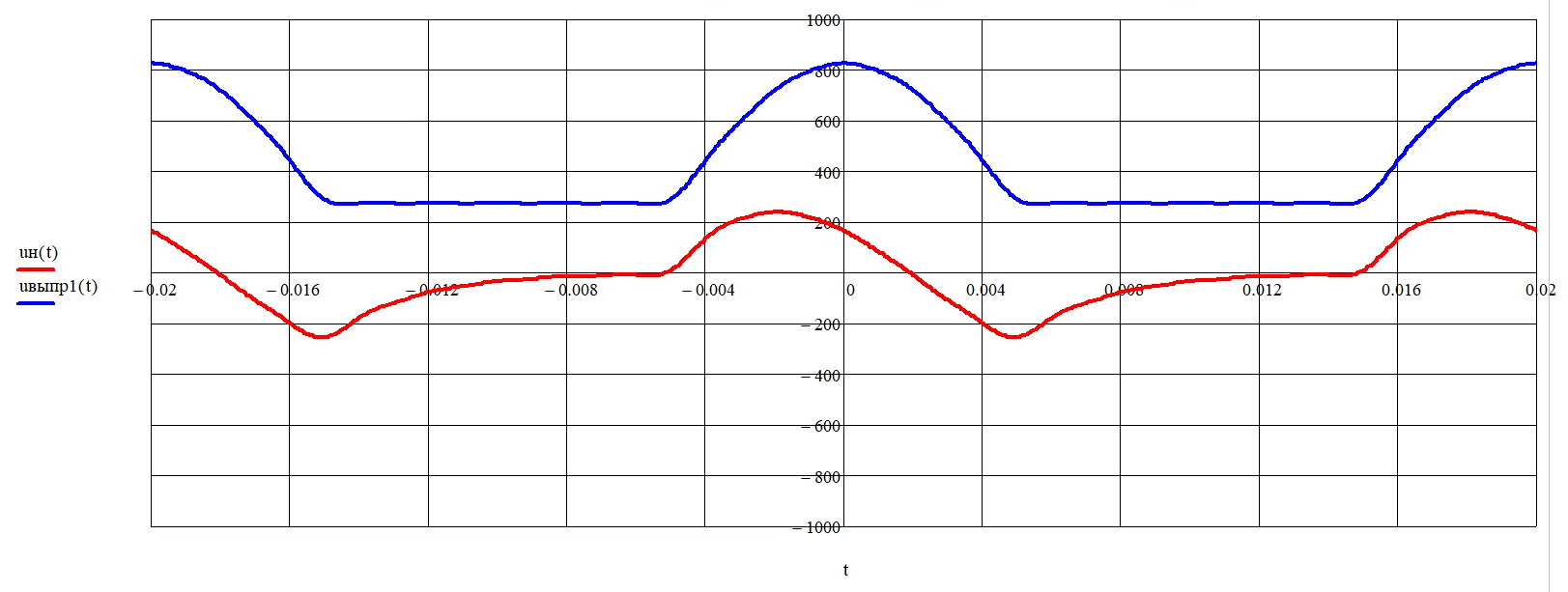
Рисунок 17 – Формы кривых напряжения нагрузки uН(t) и выходного напряжения полупроводникового выпрямителя uвыпр(t)
С помощью встроенной панели инструментов «График» отобразим амплитуды гармонических составляющих ряда Фурье в зависимости от номера гармоники и получим график спектра амплитуд (рис. 18) напряжения нагрузки.
Значения начальных фаз гармонических составляющих ряда Фурье отобразим в градусах и получим график спектра фаз (рис. 19) напряжения нагрузки.
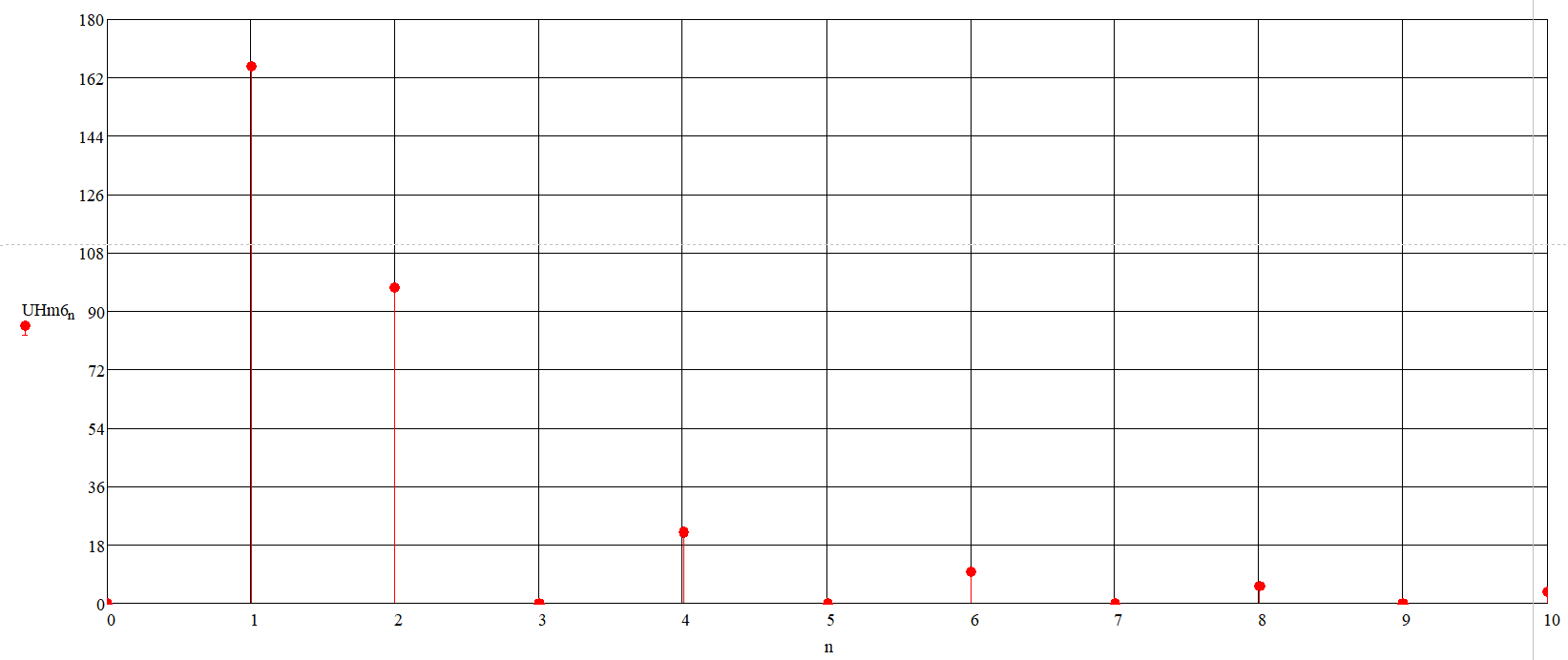
Рисунок 18 – Дискретный спектр амплитуд напряжения нагрузки
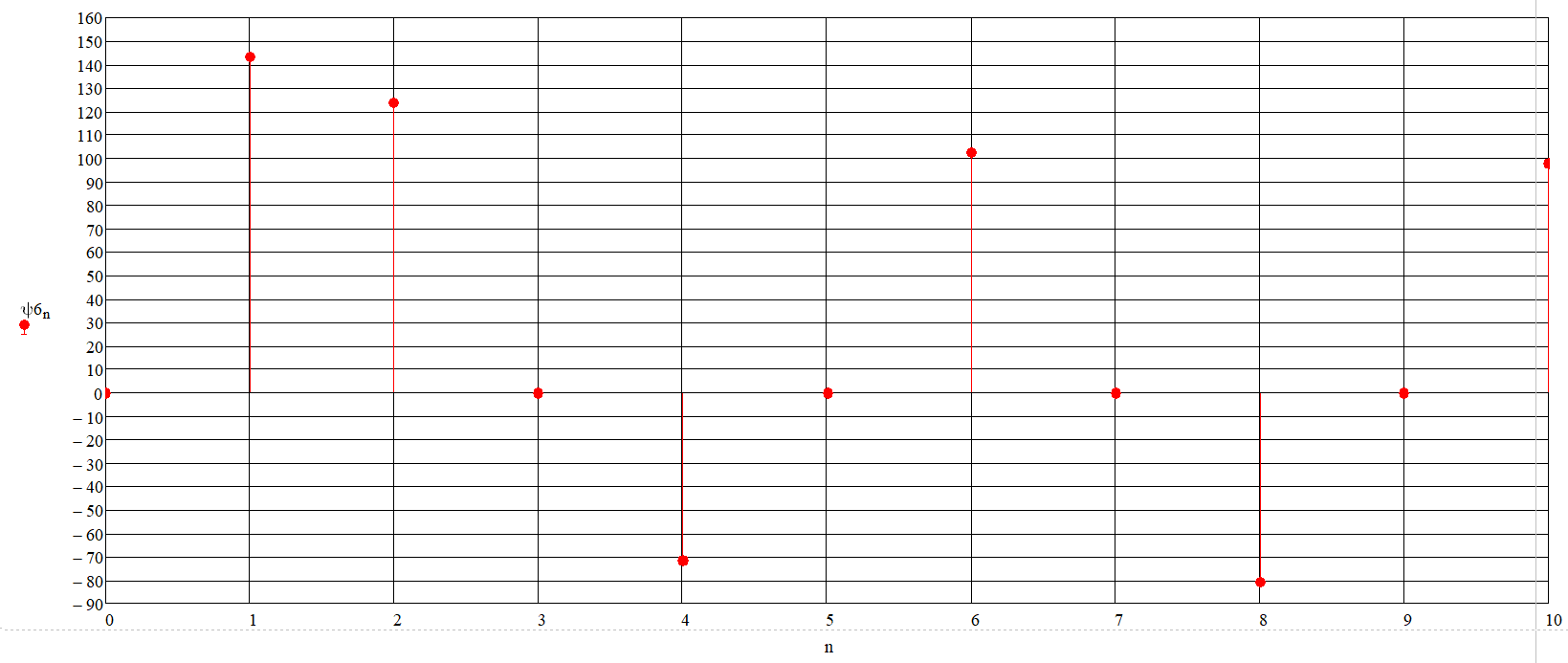
Рисунок 19 – Дискретный спектр фаз напряжения нагрузки
Действующее значение несинусоидального напряжения найдем по формуле 33.
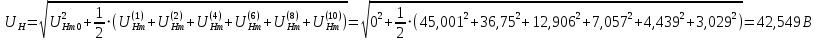 (33)
(33)Определим коэффициент искажения несинусоидального напряжения (формула 34).
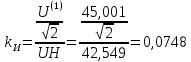 (34)
(34)По расчету видно, что значение коэффициента искажения почти равно единице, то есть форма напряжения нагрузки близка к синусоидальной, что соответствуют графику напряжению на рисунке 17.
Вывод: В данной расчётно-графической работе был исследован однополупериодный выпрямитель с полосовым фильтром.
Разложил в ряд Фурье форму кривой выходного напряжения полупроводникового выпрямителя, построил кривую напряжения, спектр амплитуд и фаз полученного сигнала. Рассчитал напряжение от каждой составляющей ряда Фурье, в нагрузочном резисторе. Записал полученные выражения для тока и напряжения
, построил соответствующие кривые. Построили спектры амплитуд и фаз полученного сигнала и определил значение тока и напряжения на нагрузке. Определил действующее значение тока и напряжения на нагрузке. Изобразил схему заграждающего L-C-фильтра и записали полученные выражения тока и напряжения на нагрузке, построили кривую напряжения и тока.