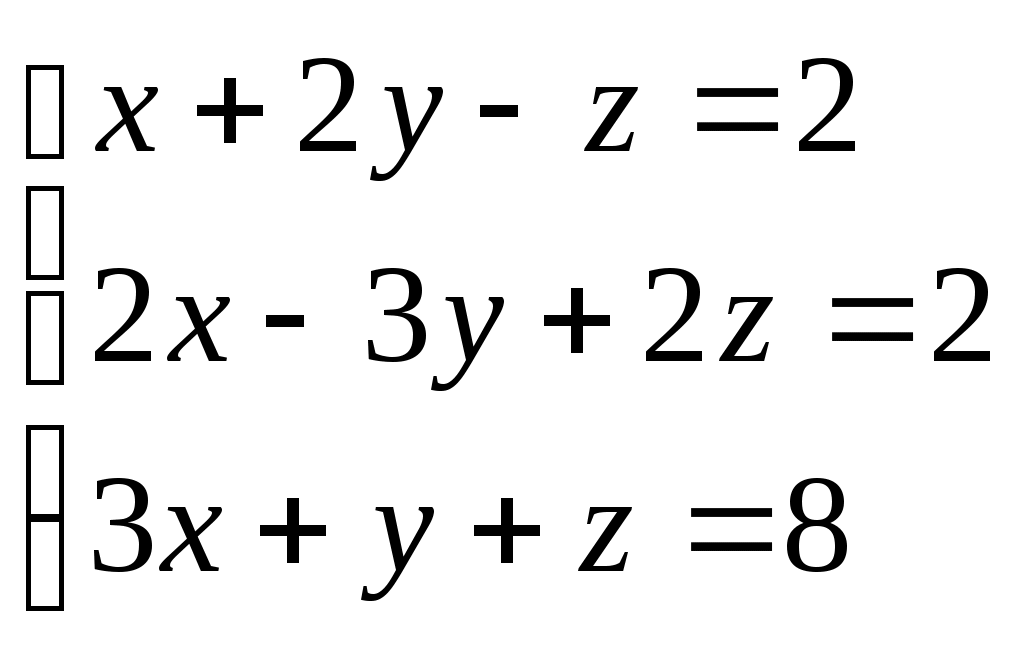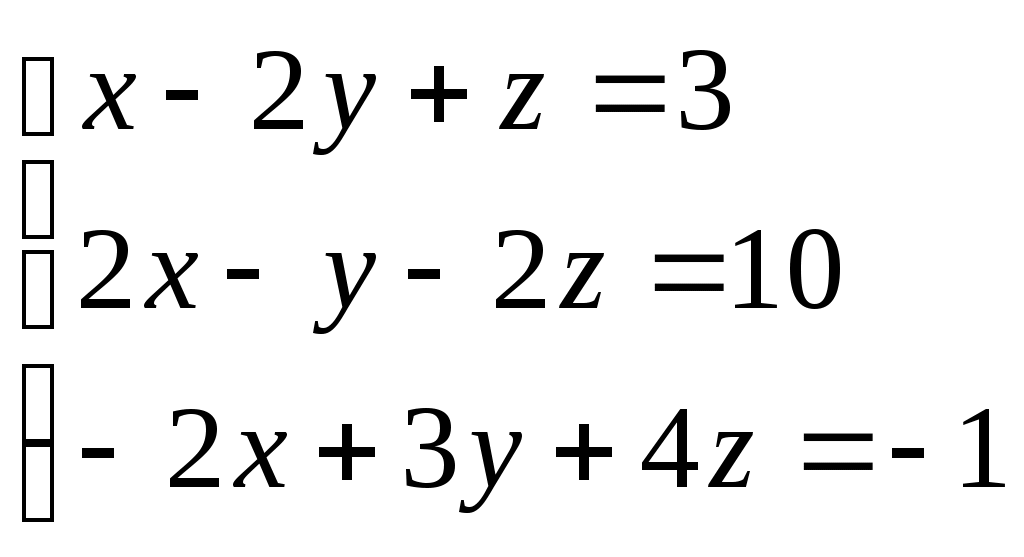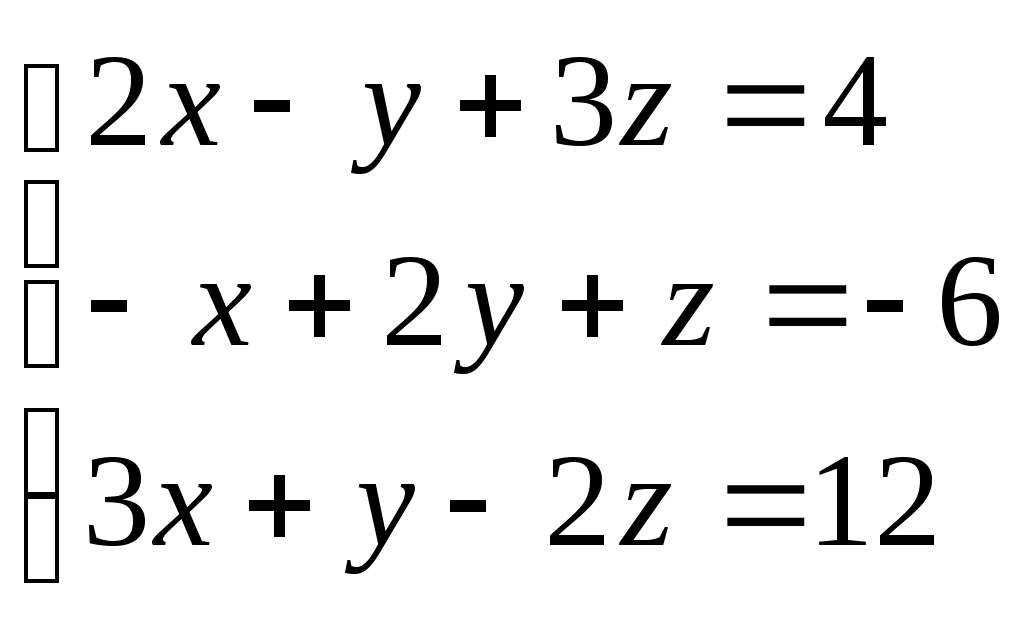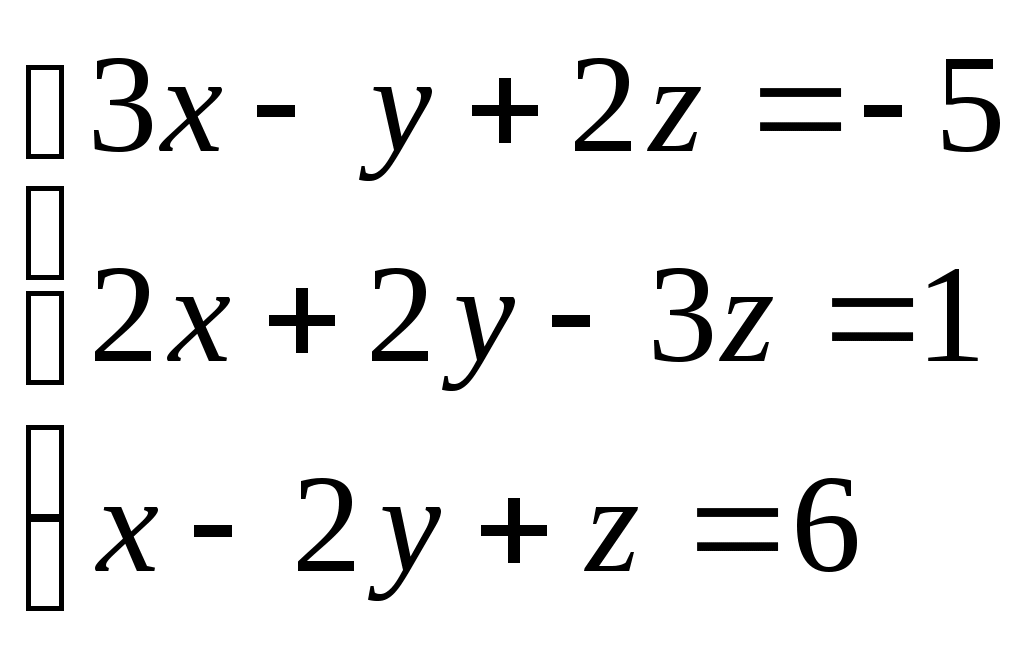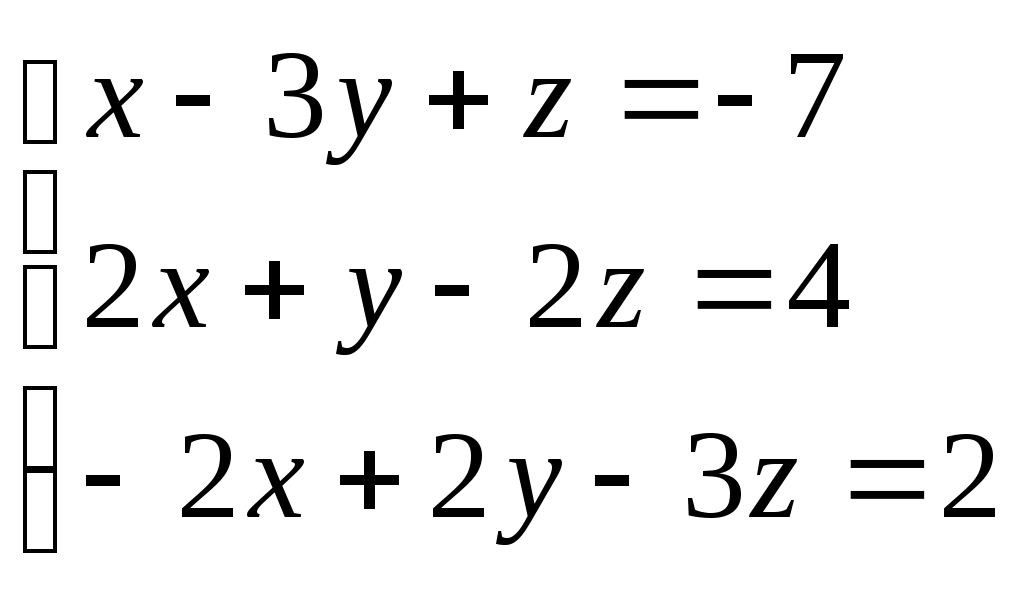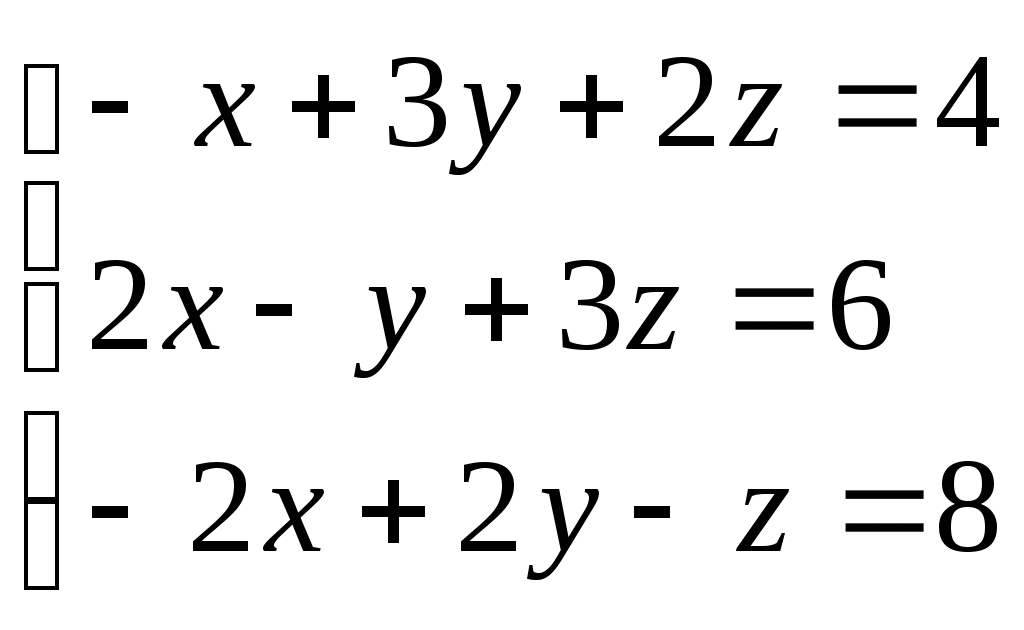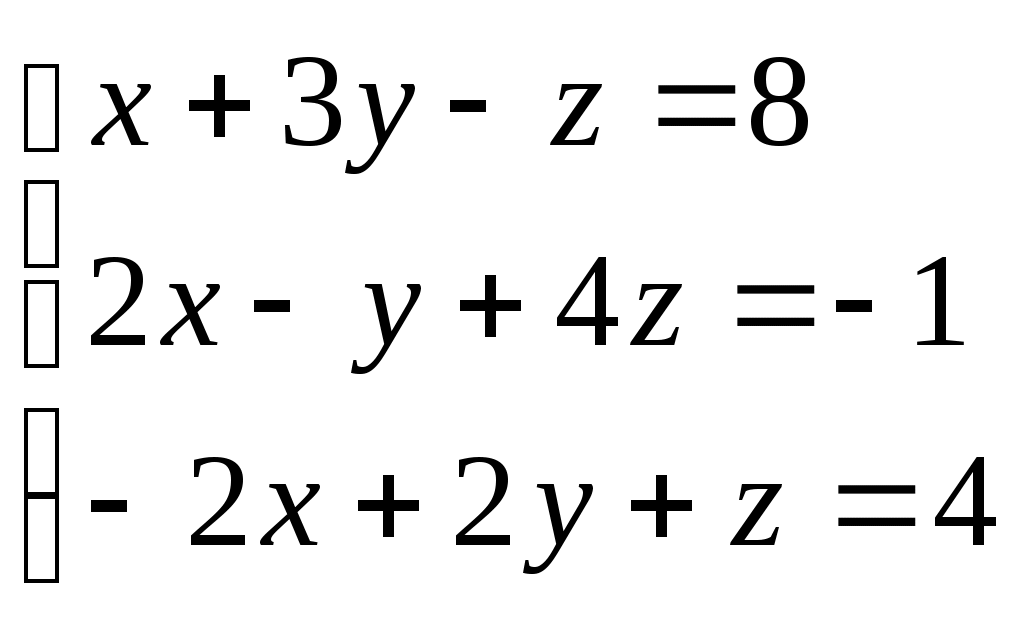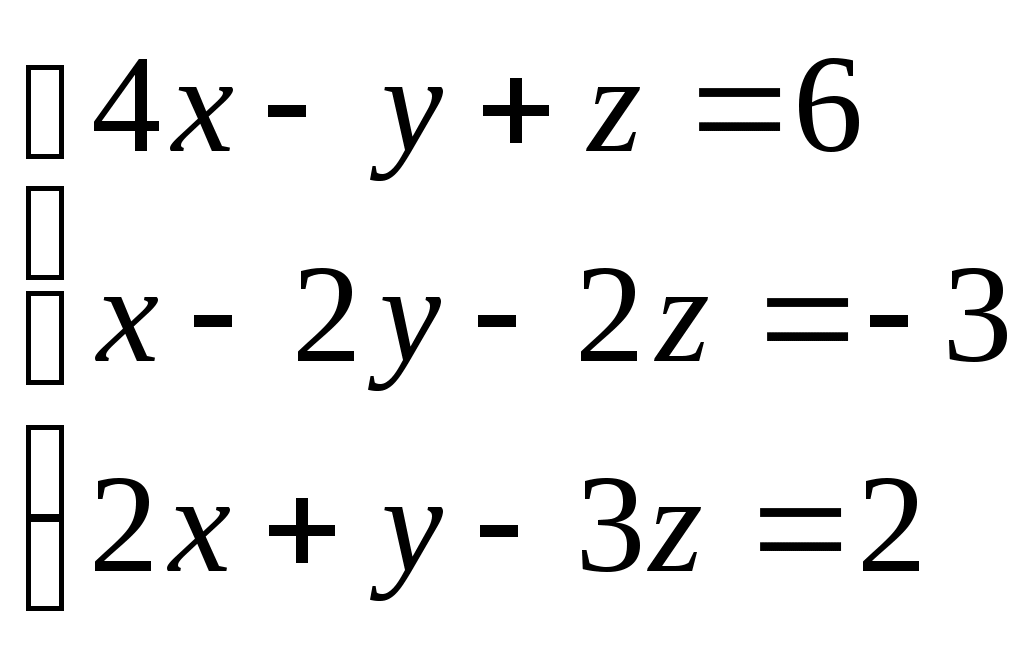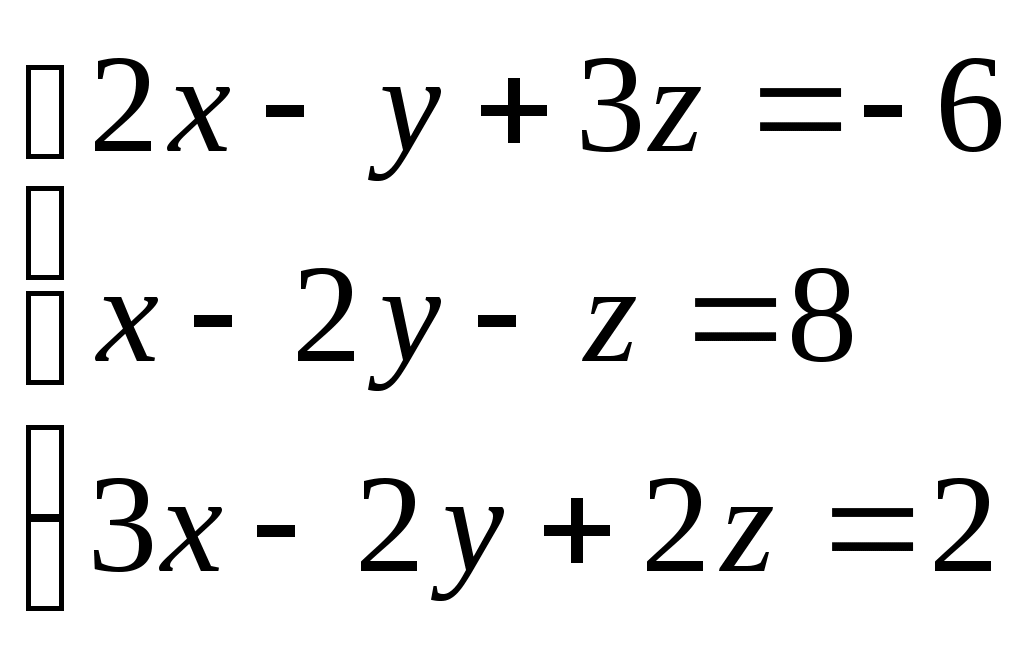Файл: Контрольная работа по дисциплине Математика для студентов ноу спо фэк специальности.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 26.10.2023

Просмотров: 108

Скачиваний: 5

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Рекомендации по выполнению контрольной работы

Рекомендуемая литература

Интернет-ресурсы



Задание № 5. Решить систему линейных алгебраических уравнений методом Крамера.

Варианты:




















Задание № 6.

Решить 3 системы методом Гаусса (в табл. 5даны элементы расширенных матриц систем 4-х уравнений с 4-мя неизвестными).

Таблица 5 – Варианты задания 6.

2
1
3
1
11

1
-1
0
1
7

3
7
-1
3
29

1
2
0
1
5




2
1
-1
3
-8

1
1
1
-2
-5

3
2
0
1
-14

-1
3
1
-1
5




2
1
-11
3
9

1
1
1
-2
2

3
2
0
1
-14

-1
3
1
-2
5






2
1
-1
3
8

1
-1
4
-3
-4

3
2
0
1
-14

-1
3
1
-1
5




5
-3
2
1
9

1
-1
4
-3
-1

2
-3
0
-3
2

3
0
2
4
7




3
2
1
0
3

1
0
4
-1
1

2
2
0
1
3

3
1
-3
2
4






2
2
3
1
11

1
-1
0
1
7

3
7
-1
3
29

2
1
0
2
12




3
2
4
0
4

1
0
4
-1
1

2
2
0
1
3

3
1
-3
2
1




2
1
3
3
7

1
0
4
-1
1

2
2
0
1
3

3
1
-3
2
4






5
-3
2
1
9

1
-1
4
-3
-1

2
1
-3
1
2

3
0
2
4
7




-3
0
1
2
-5

-3
1
3
1
2

4
-3
2
1
3

0
1
2
1
7




2
-1
3
1
2

1
2
3
-2
5

-1
1
2
3
2

0
3
5
-5
10






2
1
3
1
11

1
-1
0
1
7

3
7
-1
3
29

2
1
0
2
14




2
1
3
3
7

1
-1
0
4
-1

2
-1
0
7
0

1
0
0
3
1




-1
1
0
2
4

3
-2
1
4
4

2
-1
1
6
6

2
0
1
-1
-2






3
-1
1
4
2

1
0
4
-1
1

2
2
0
1
3

3
1
-3
2
1




2
-1
3
1
3

1
2
3
-2
5

-1
1
2
-3
2

0
3
5
-5
7




2
1
3
1
5

2
1
-5
-1
2

4
2
-2
0
-6

3
-1
1
5
-2






5
-3
2
1
9

1
-1
4
-3
-1

2
-3
0
-3
5

1
0
2
4
7




-1
1
2
2
2

3
-2
1
4
4

2
-1
1
5
6

2
0
1
-1
-2




1
4
6
-1
5

1
3
1
-3
3

0
1
2
-1
11

-1
-2
1
3
-11






-3
0
1
2
-5

1
-1
-2
1
-4

4
-3
2
1
3

0
1
2
-1
7




2
1
3
1
5

2
1
-6
-1
-1

4
2
-2
0
-6

3
-1
1
5
-2




1
2
0
3
4

-5
-3
1
-1
3

-3
1
2
2
12

6
5
-1
4
-6






2
1
3
3
7

1
1
0
4
-1

3
0
7
9
10

1
0
0
3
1




1
4
6
-4
10

1
3
4
-3
9

0
1
2
-1
1

-1
-2
1
2
-14




-1
3
5
4
-9

1
-1
1
1
2

1
-1
-2
1
-1

1
-1
4
1
-7






2
-1
3
1
8

1
2
3
-2
5

-1
1
2
-3
2

2
-1
1
3
4




1
-1
4
1
-5

2
3
2
3
18

1
2
2
1
9

0
1
2
-1
0




2
-5
3
-1
0

3
-7
3
-1
2

1
-9
6
7
3

4
-16
9
6
7






Задание № 7.

Z1, Z2 – комплексные числа. Выполнить действия:

А) Z1+ Z2; Б) Z1Z2; В) Z1/Z2.

Варианты:

  1. Z1=5–4i; Z2=-1-i.

  1. Z1=-6+3i; Z2=2-i.

  1. Z1=3–2i; Z2=-45+i.

  1. Z1=4–3i; Z2=1-i.

  1. Z1=2–i; Z2=5-3i.

  1. Z1=3+2i; Z2=-3+4i.

  1. Z1=5–i; Z2=4-3i.

  1. Z1=6–2i; Z2=-1-4i.

  1. Z1=1–5i; Z2=-3+2i.

  1. Z1=5+2i; Z2=-3-2i.


Задание № 8. Записать комплексное число в тригонометрической и показательной формах.

Варианты:

  1. Z=-1-2i.

  1. Z=-1-i.

  1. Z=1+2i.

  1. Z=3+i.

  1. Z=2+i.

  1. Z=1-i.

  1. Z=2-i.

  1. Z=4-3i.

  1. Z=3-2i.

  1. Z=2+2i.


Задание № 9. Вычислить указанные пределы, не используя правило Лопиталя.

Варианты:


А) X0 = 1
Б) X0 = 2
В) X0 = 





А) X0 = 3
Б) X0 = -1
В) X0 = 





А) X0 = 3
Б) X0 = 1
В) X0 = 





А) X0 = 2
Б) X0 = 1
В) X0 = 





А) X0 = -1
Б) X0 = 1
В) X0 = 





А) X0 = -2
Б) X0 = 1
В) X0 = 





А) X0 = 1
Б) X0 = -1
В) X0 = 





А) X0 = 2
Б) X0 = 3
В) X0 = 





А) X0 = 3
Б) X0 = -3
В) X0 = 





А) X0 = -3
Б) X0 = -2
В) X0 = 


Задание № 10. Найти производные функций.

Варианты:
А) ; В) ;
Б) ; Г)



А) ; В) ;
Б) ; Г)



А) ; В) ;
Б) ; Г)



А) ; В) ;
Б) ; Г)



А) ; В) ;
Б) ; Г)



А) ; В) ;
Б) ; Г)



А) ; В) ;
Б) ; Г)



А) ; В) ;
Б) ; Г)



А) ; В) ;
Б) ; Г)



А) ; В) ;
Б) ; Г)


Задание № 11. Исследовать данную функцию методами дифференциального исчисления и построить ее график.

Варианты:




















Задание № 12. Вычислить неопределенные интегралы.

Варианты:
А) ;
Б) ;
В) .



А) ;
Б) ;
В) .



А) ;
Б) ;
В) .



А) ;
Б) ;
В) .



А) ;
Б) ;
В) .



А) ;
Б) ;
В) .



А) ;
Б) ;
В)



А) ;
Б) ;
В)



А) ;
Б) ;
В) .



А) ;
Б) ;
В) .

Смотрите также файлы