ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 1004
Скачиваний: 5
3.
Основы
теории
пластичности
Условие
пластичности
Пластические
деформации
возникают
при
достижении
некоторой
комбинации
напряжений
определенного
предельного
значения
( )
.
0
=
ij
f
σ
Функция
называется
условием
пластичности
.
Для
дальнейшего
рассмотрения
удобно
ввести
пространство
напряжений
П
тензора
.
Шестимерное
пространство
П
определим
как
пространство
,
в
котором
декартовы
координаты
точки
равны
компонентам
тензора
напряжений
.
j
( )
ij
f
σ
ij
σ
ij
σ
д
р
рд
р
р
р
Аналогично
можно
ввести
пространство
деформаций
Э
,
соответствующее
тензору
деформации
,
и
пространство
скоростей
деформации
Е
,
соответствующее
тензору
скоростей
деформации
.
Условию
пластичности
в
пространстве
напряжений
П
соответствует
ij
е
ij
ε
р
р
р
у
некоторая
поверхность
,
называемая
поверхностью
пластичности
.
Область
Q,
лежащая
внутри
поверхности
,
является
областью
упругого
состояния
материала
.
Напряженные
состояния
,
соответствующие
точкам
области
Q,
не
достигающим
границы
,
не
вызывают
остаточных
∑
∑
∑
р
деформаций
.
Основные
постулируемые
свойства
поверхности
пластичности
состоят
в
следующем
:
она
замкнута
(
в
некоторых
направлениях
может
простираться
до
бесконечности
),
не
проходит
через
начало
координат
и
любой
луч
,
д
),
р
д
р
рд
у
,
исходящий
из
начала
координат
,
пересекает
ее
не
более
одного
раза
.
Условия
пластичности
изотропного
пластического
тела
Условие
пластичности
максимального
касательного
напряжения
(
Треска
)
записывается в виде
напряжения
(
Треска
)
записывается
в
виде
где
tmax —
максимальное
касательное
напряжение
.
Условие пластичности Треска интерпретируется в
{
}
k
=
−
−
−
=
1
3
3
2
2
1
max
,
max
2
1
σ
σ
σ
σ
σ
σ
τ
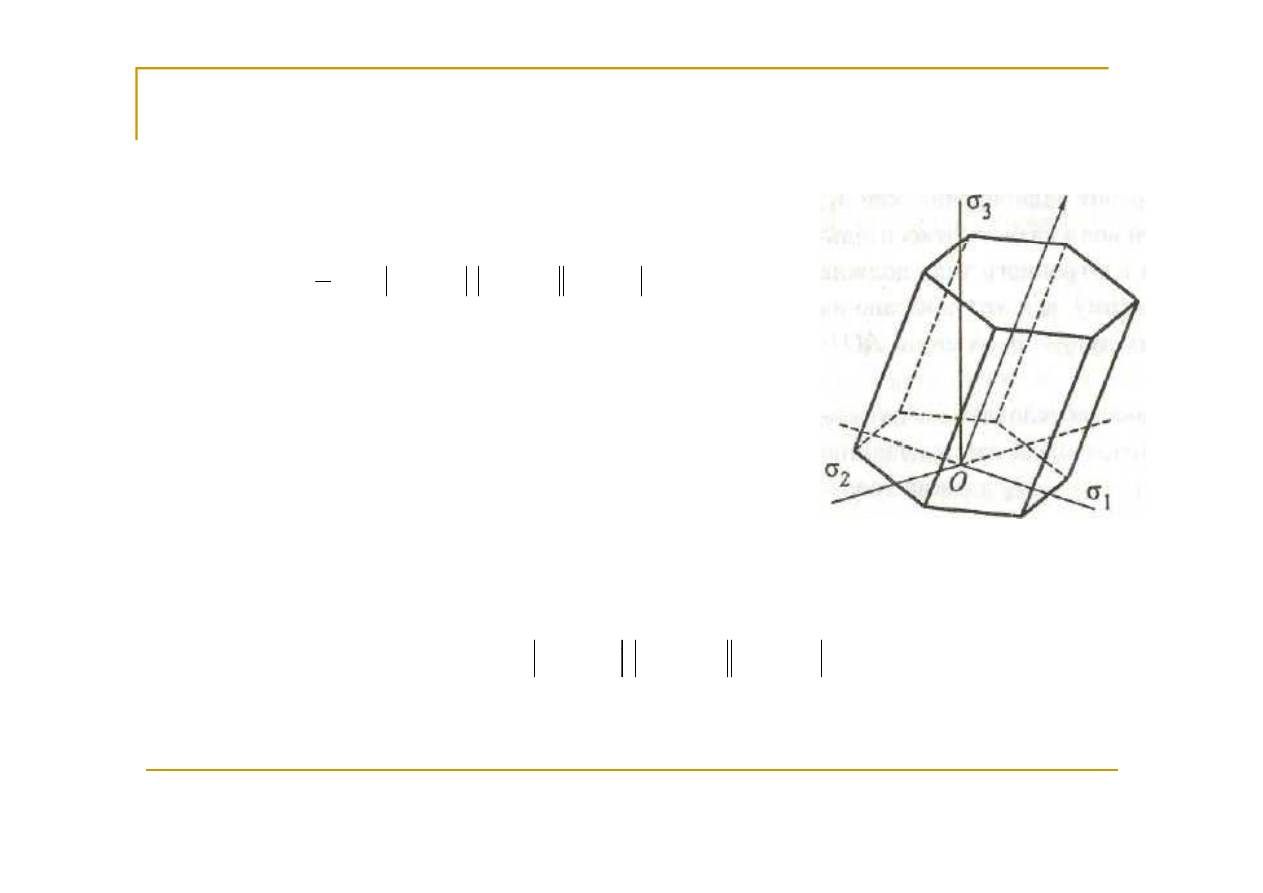
Условие
пластичности
Треска
интерпретируется
в
пространстве
главных
напряжений
шестигранной
призмой
,
равнонаклоненной
к
осям
координат
.
Условие
пластичности
октаэдрического
напряжения
(
Мизеса
)
записывается в виде
(
Мизеса
)
записывается
в
виде
Условие
пластичности
Мизеса
интерпретируется
в
пространстве главных напряжений круговым
П
Т
С
В
k
ij
ij
=
=
∑
/
/
2
σ
σ
пространстве
главных
напряжений
круговым
цилиндром
,
образующие
которого
равнонаклонены
к
осям
координат
.
Призма
Треска
-
Сен
-
Венана
Условие
пластичности
максимального
приведенного
напряжения записывается
в
виде
{
}
k
где
smax —
максимальное
приведенное
напряжение
.
Условие
пластичности
максимального
приведенного
напряжения
интерпретируется
в
пространстве
главных
напряжений
шестигранной
призмой
,
равнонаклоненной
к
осям
координат
.
{
}
k
s
=
−
−
−
=
σ
σ
σ
σ
σ
σ
3
2
1
max
,
max
Деформационная
теория
пластичности
ф р
р
Рассмотрим
уравнения
пластической
деформации
как
некоторое
обобщение
закона
Гука
.
Примем
следующие
исходные
положения
:
-
тело
изотропно
;
-
относительное
изменение
объема
является
упругой
деформацией
,
пропорциональной
среднему
давлению
:
-
девиаторы
деформации
и
напряжения
пропорциональны
Девиаторы
деформации
и
напряжения
имеют
одни
и
те
же
главные
направления
,
а
3
K
ε
σ
=
;
D
D
ε
σ
ψ
=
.
их
главные
значения
соответственно
пропорциональны
:
Полагая
,
представим
компоненты
деформации
в
виде
суммы
компонент
упругой
и
пластической
деформации
При
исключении
объемного
расширения
в
уравнении
,
находим
соотношения
Генки
1 2 3
i
i
e
s i
ψ
=
= , , .
1 (2 )
ψ
μ φ
= /
+
e
ij
ε
p
p
ij
ij
ij
e
s
ε
φ
=
=
.
Эти
соотношения
нетрудно
разрешить
и
относительно
напряжений
:
ij
ij
ij
K
s
ε
σδ ψ
=
+
.
1
3
ij
ij
ij
e
K
ε
σ
δ
ψ
=
+
.
Вычисляя
интенсивность
деформаций
сдвига
,
получаем
важное
соотношение
Полученные
уравнения
не
являются
полными
,
так
как
содержат
неизвестную
функцию
.
Возьмем
в
качестве
дополнительного
соотношения
условие
текучести
2
T
ψ
Γ =
.
ψ
фу ц
д
у
у
Мизеса
:
В
этом
случае
Тогда
находим
Напряжения
,
представленные
этими
формулами
, –
однозначные
функции
компонент
деформации
и
тождественно
удовлетворяют
условию
текучести
Мизеса
.
ψ
s
T
τ
= .
2
s
ψ
τ
Γ
=
.
2
3
s
ij
ij
ij
e
K
τ
ε
σ
δ
=
+
.
Γ
у
у
у
Теория
пластического
течения
р
Уравнения
теории
пластического
течения
устанавливают
связь
между
бесконечно
малыми
приращениями
деформаций
,
приращениями
напряжений
и
самими
напряжениями
.
р
Исходные
положения
этой
теории
:
-
тело
изотропно
;
-
относительное
изменение
объема
мало
и
является
упругой
деформацией
,
пропорциональной
среднему
давлению
:
3
K
ε
σ
=
.
р
рц
р д
у д
-
приращения
составляющих
упругой
деформации
связаны
с
приращениями
составляющих
напряжения
законом
Гука
:
-
девиатор напряжения
и девиатор приращения пластической деформации
1
3
(
)
2
1
e
ij
ij
ij
d
d
d
ν
ε
σ
δ σ
μ
ν
=
−
;
+
D
p
d
D
ε
девиатор
напряжения
и
девиатор
приращения
пластической
деформации
пропорциональны
,
т
.
е
.
где
–
некоторый
бесконечно
малый
множитель
.
Справедливы соотношения
σ
p
d
D
d D
ε
σ
λ
=
,
d
λ
Справедливы
соотношения
Вычисляя
приращение
работы
пластической
деформации
,
находим
В общем случае эти уравнения не являются полными так как содержат неизвестный
p
ij
ij
d
d s
ε
λ
=
.
2
2
p
p
ij
ij
ij ij
dA
d
d
s
d T
σ ε
λσ
λ
=
=
=
.
В
общем
случае
эти
уравнения
не
являются
полными
,
так
как
содержат
неизвестный
множитель
,
для
определения
которого
нужно
располагать
дополнительным
соотношением
,
в
роли
которого
используется
условие
текучести
.
Уравнения
теории
пластического
течения
с
условием
текучести
Мизеса
называют
моделью
Прандтля
-
Рейса
.
д
р д