ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.04.2021
Просмотров: 242
Скачиваний: 1
Итак
,
в
оболочечной
модели
одночастичные
состояния
характеризуются
следующими
квантовыми
числами
:
n, l, j, m
,
где
n
-
главное
квантовое
число
(
оно
нумерует
одночастичные
орбиты
с
одинаковыми
lj
в
порядке
возрастания
их
энергии
);
l
-
орбитальный
момент
количества
движения
нуклона
;
j
-
полный
момент
количества
движения
нуклона
и
m
-
проекция
этого
момента
на
ось
z
.
С
целью
учёта
коллективных
состояний
,
в
оболочечную
модель
вводится
понятие
квазичастиц
-
элементарных
возбуждений
среды
,
эффективно
ведущих
себя
во
многих
отношениях
подобно
частицам
.
При
этом
ядро
рассматривается
как
квантовая
жидкость
,
точнее
как
ферми
-
жидкость
конечных
размеров
.
Ядро
в
основном
состоянии
рассматривается
как
вырожденный
ферми
-
газ
квазичастиц
,
которые
эффективно
не
взаимодействуют
друг
с
другом
,
поскольку
всякий
акт
столкновения
,
изменяющий
индивидуальные
состояния
квазичастиц
,
запрещён
принципом
Паули
.
В
возбуждённом
состоянии
ядра
,
когда
1
или
2
квазичастицы
находятся
на
более
высоких
индивидуальных
энергетических
уровнях
,
эти
частицы
,
освободив
орбиты
,
занимавшиеся
ими
ранее
внутри
ферми
-
сферы
,
могут
взаимодействовать
как
друг
с
другом
,
так
и
с
образовавшейся
дыркой
в
нижней
оболочке
.
В
результате
взаимодействия
с
внешней
квазичастицей
может
происходить
переход
квазичастиц
из
заполненных
состояний
в
незаполненное
,
вследствие
чего
старая
дырка
исчезает
,
а
новая
появляется
;
это
эквивалентно
переходу
дырки
из
одного
состояния
в
другое
.
Рис
. 7.
Изменение
потенциалов
нейтрон
-
ядро
и
протон
-
ядро
взаимодействий
в
зависимости
от
расстояния
частицы
от
центра
ядра
.
Согласно
оболочечной
модели
,
основывающейся
на
теории
квантовой
ферми
-
жидкости
,
спектр
нижних
возбуждённых
состояний
ядер
определяется
движением
1-2
квазичастиц
вне
ферми
-
сферы
и
взаимодействием
их
друг
с
другом
и
с
дырками
внутри
ферми
-
сферы
.
Этим
самым
объяснение
структуры
многонуклонного
ядра
при
небольших
энергиях
возбуждения
фактически
сводится
к
квантовой
проблеме
2-4
взаимодействующих
тел
(
квазичастица
-
дырка
или
2
квазичастицы
- 2
дырки
).
Трудность
теории
состоит
в
том
,
что
взаимодействие
квазичастиц
и
дырок
не
мало
и
потому
нет
уверенности
в
невозможности
появления
низкоэнергетического
возбуждённого
состояния
,
обусловленного
большим
числом
квазичастиц
вне
ферми
-
сферы
.
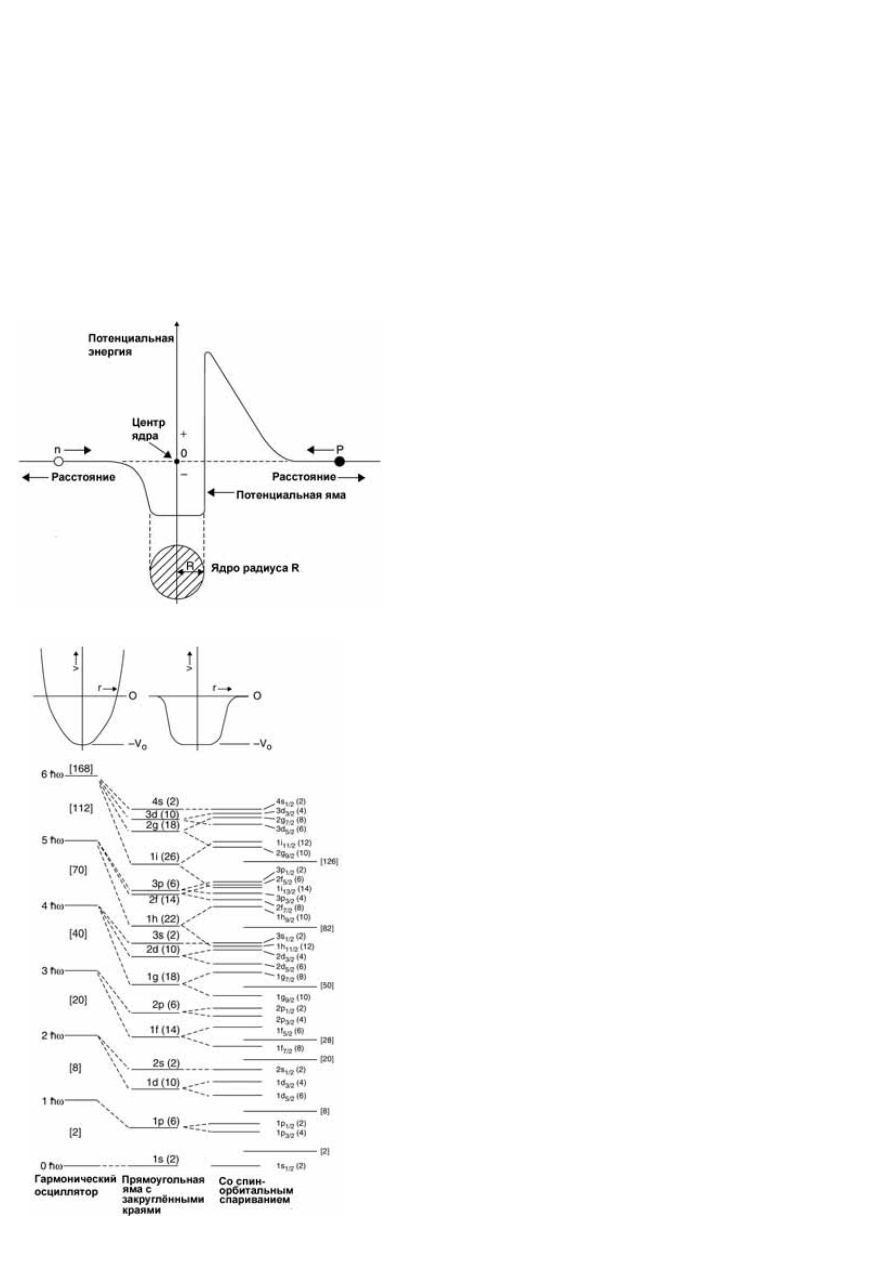
Рис
. 8.
Энергии
одно
-
частичных
орбит
в
гармоническом
осцилляторе
и
прямоугольной
потенциальной
яме
со
скруглёнными
краями
(
в
последней
–
с
и
без
спин
-
орбитального
спаривания
).
Цифры
в
круглых
скобках
–
ёмкость
орбит
,
а
в
квадратных
скобках
–
кумулятивная
ёмкость
выше
данной
точки
.
3.3
Ядерные
потенциалы
и
энергетические
уровни
ядра
Комбинированное
взаимодействие
нейтронов
и
протонов
может
быть
описано
в
терминах
«
ядерной
потенциальной
ямы
».
Поскольку
протоны
–
заряженные
частицы
,
а
нейтроны
–
нет
,
рассматривают
протоны
и
нейтроны
,
так
как
будто
они
находятся
в
отдельных
потенциальных
ямах
(
суперпозиция
ям
).
Это
–
простая
схема
описания
сил
,
действующих
на
нейтрон
,
вброшенный
в
ядро
.
На
больших
расстояниях
(
более
нескольких

фемтометров
)
никаких
сил
нет
(
нет
изменений
в
потенциальной
энергии
).
Когда
нейтрон
достигает
«
поверхности
»
ядра
(
или
попадает
под
действие
ядерных
сил
на
расстоянии
примерно
1
фм
от
«
края
»
ямы
),
происходит
взаимодействие
с
ближайшими
нуклонами
,
и
нейтрон
захватывается
ядром
.
Это
взаимодействие
быстро
увеличивается
в
приповерхностной
области
по
мере
того
,
как
нуклон
входит
в
контакт
с
другими
нуклонами
,
до
тех
пор
,
пока
они
не
окружат
его
,
и
он
не
окажется
внутри
ядра
.
Потенциальная
энергия
остаётся
практически
постоянной
пока
нуклон
движется
внутри
ядра
и
не
приближается
к
его
краям
.
Другое
поведение
имеет
место
при
внесении
в
ядро
протона
.
Ядро
сначала
отталкивает
протон
дальнодействующими
кулоновскими
силами
.
Только
при
приближении
протона
почти
вплотную
к
поверхности
ядерное
взаимодействие
начинает
пересиливать
отталкивание
.
Ядерное
взаимодействие
будет
усиливаться
до
тех
пор
,
пока
протон
не
окажется
окружённым
нуклонами
,
как
это
было
и
в
случае
нейтрона
,
но
в
данном
случае
всегда
будет
набор
отталкиваний
со
стороны
других
протонов
.
Отталкивание
уменьшает
общее
взаимодействие
,
поэтому
потенциальная
яма
протона
не
столь
же
глубока
,
как
у
нейтрона
.
В
отличие
от
свободных
частиц
,
для
которых
энергия
может
принимать
любые
значения
(
так
называемый
непрерывный
спектр
),
связанные
частицы
(
то
есть
частицы
,
кинетическая
энергия
которых
меньше
потенциальной
),
могут
находиться
в
состояниях
только
с
определёнными
дискретными
значениями
энергий
-
дискретный
спектр
.
Так
как
ядро
-
система
связанных
нуклонов
,
оно
обладает
дискретным
спектром
энергий
.
Обычно
оно
находится
в
наиболее
низком
энергетическом
состоянии
,
называемым
основным
.
Если
передать
ядру
энергию
,
оно
перейдёт
в
возбуждённое
состояние
.
Расположение
энергетических
уровней
ядра
в
первом
приближении
:
,
*
E
ae
D
=
(16)
где
:
D
-
среднее
расстояние
между
уровнями
,
E
* -
энергия
возбуждения
ядра
,
a
и
b
-
коэффициенты
,
постоянные
для
данного
ядра
:
a
-
среднее
расстояние
между
первыми
возбуждёнными
уровнями
(
для
лёгких
ядер
примерно
1
МэВ
,
для
тяжёлых
- 0,1
МэВ
),
b
-
константа
,
определяющая
скорость
сгущения
уровней
при
увеличении
энергии
возбуждения
(
для
лёгких
ядер
примерно
2
МэВ
−
1/2
,
для
тяжёлых
- 4
МэВ
−
1/2
).
С
ростом
энергии
возбуждения
уровни
сближаются
быстрее
у
тяжёлых
ядер
,
чем
у
лёгких
.
Плотность
уровней
зависит
от
чётности
числа
нейтронов
в
ядре
.
Для
ядер
с
чётными
(
особенно
магическими
)
числами
нейтронов
плотность
уровней
меньше
,
чем
для
ядер
с
нечётными
,
при
равных
энергиях
возбуждения
первый
возбуждённый
уровень
в
ядре
с
чётным
числом
нейтронов
расположен
выше
,
чем
в
ядре
с
нечётным
.
Рис
. 9.
Одночастичные
энергетические
уровни
в
облочечном
потенциале
и
спектроскопические
обозначения
состояний
в
грубой
оболочечной
модели
.
Угловые
моменты
спаривания
представлены
на
левой
стороне
,
а
числа
нуклонов
,
необходимые
для
заполнения
каждой
орбиты
и
каждой
оболочки
–
на
правой
стороне
.
Приведено
схематическое
изображение
уровней
в
потенциале
Вудса
-
Саксона
:
слева
без
учета
спин
-
орбитального
взаимодействия
,
справа
-
с
учетом
.
Фигурные
скобки
объединяют
уровни
,
входящие
в
одну
осцилляторную
оболочку
.
В
круглых
скобках
дано
число
вакантных
мест
для
нуклонов
одного
сорта
,
в
квадратных
скобках
приведено
полное
число
частиц
.
Форму
ядерного
потенциала
можно
определить
методами
квантовой
механики
на
базе
оболочечной
модели
ядра
.
Для
грубой
оценки
состояний
,
которые
«
заполняют
»
потенциальную
яму
,
можно
представить
ядро
,
как
набор
некоторых
конечных
уровней
–
стационарных
состояний
или
орбиталей
,
аналогично
электронам
в
потенциальной
яме
атома
.
Эта
интерпретация
переносит
на
ядро
атомную
оболочечную
модель
.
Следует
,
однако
,
помнить
,
что
ядро
коренным
образом
отличается
от
атома
,
поэтому
можно
ожидать
,
что
и
энергетические
уровни
и
их
заполнения
в
ядре
будут
другими
,
чем
в
атоме
.
В
качестве
первого
приближения
ядро
рассматривают
как
сферический
жёсткий
контейнер
(
прямоугольная
потенциальная
яма
).
Потенциальная
энергия
предполагается
точно
равной
нулю
,
если
частица
находится
в
пределах
стен
контейнера
и
стены
так
прочны
и
высоки
,
что
частица
не
может
их
преодолеть
.
Аналогией
является
газ
внутри
малой
сферической
ёмкости
.
Более
полезным
является
потенциал
гармонического
осциллятора
,
имеющий
параболическую
форму
.
Этот
потенциал
,
как
и
прямоугольный
,
имеет
крутые
бока
,
поэтому
полезен
только
для
низколежащих
энергетических
уровней
.
Особенность
потенциала
гармонического
осциллятора
–
эквивалентно
разнесённые
в
пространстве
энергетические
уровни
.
Этот
потенциал
не
«
насыщенный
»,
он
имеет
закруглённое
дно
,
что
не
удобно
для
описания
больших
ядер
.
Потенциал
гармонического
осциллятора
применяется
для
лёгких
ядер
,
и
волновые
функции
гармонического
осциллятора
используются
для
расчётов
ядерных
реакций
.
Состояния
гармонического
осциллятора
отмечаются
общим
угловым
моментом
,
начинающимся
с
0.
Каждый
уровень
основного
квантового
числа
формирует
оболочку
орбиталей
.
Энергетические
щели
между
оболочками
точно
одинаковы
,
и
все
подуровни
с
данным
основным
квантовым
числом
вырождены
.
Число
орбит
задаётся
выражением
2
N
+1,
где
N
=0, 1, 2,…
Принцип
Паули
требует
,
чтобы
число
нуклонов
(
фермионов
),
необходимых
для
заполнения
каждой
орбиты
было
рано
2 (
как
и
для
электронах
на
атомных
орбитах
),
поэтому
число
нуклонов
,
необходимых
для
заполнения
каждой
оболочки
,
равно
2[2
N
+1]=2, 6, 10,…
Это
заполнение
согласуется
с
увеличенной
стабильностью
легчайших
ядер
(
4
Не
,
16
О
),
в
которых
нейтроны
и
протоны
находятся
на
разных
орбитах
.
Однако
для
тяжёлых
ядер
такого
согласия
нет
.
Табл
. 3
.
Оболочки
сферического
гармонического
осциллятора
Оболочки
N
Орбиты
nl
Четность
Кратность
вырождения
Полное
число
частиц
0 1
s
+
2
2
1 1
p
-
6
8
2 2
s
, 1
d
+
12
20
3 2
p
, 1
f
-
20
40
4 3
s
, 2
d
, 1
g
+
30
70
5 3
p
, 2
f
, 1
h
-
42
112
6 4
s
, 3
d
, 2
g
, 1
i
+ 56
168
Из
Табл
. 3
видно
,
что
одночастичные
уровни
осцилляторного
потенциала
дополнительно
вырождены
по
квантовым
числам
nl
.
Это
вырождение
носит
случайный
характер
.
При
изменении
формы
потенциала
V(r)
-
например
,
при
использовании
прямоугольной
потенциальной
ямы
-
состояния
с
разными
l,
входящие
в
одну
и
ту
же
осцилляторную
оболочку
,
расщепляются
по
энергии
,
причём
вниз
опускаются
состояния
с
максимальными
l
,
поскольку
переход
от
осцилляторной
ямы
к
прямоугольной
означает
углубление
ямы
по
краям
,
где
находятся
частицы
с
большими
значениями
l
.
Из
таблицы
также
видно
,
что
осцилляторные
оболочки
заполняются
при
числах
нуклонов
,
равных
2, 8, 20, 40, 70, 112
и
168.
Только
три
первых
члена
этой
последовательности
совпадают
с
наблюдаемыми
в
эксперименте
магическими
числами
.
Это
указывает
на
необходимость
модификации
оболочечного
потенциала
.
Как
видно
из
Рис
. 9
,
ядерные
оболочки
отделены
друг
от
друга
широкими
(
ћω
/2)
энергетическими
интервалами
.
Это
объясняет
особенную
стабильность
магических
ядер
,
имеющих
в
основном
состоянии
заполненные
нейтронные
и
(
или
)
протонные
оболочки
.
Простой
потенциал
гармонического
осциллятора
был
улучшен
добавлением
спин
-
орбитальной
корреляции
.
Релятивистские
частицы
имеют
тенденцию
выравнивать
свои
орбитальные
и
внутренние
угловые
моменты
(
спины
).
Добавление
спин
-
орбитального
члена
в
ядерный
потенциал
гармонического
осциллятора
приводит
к
разделению
или
удалению
вырожденности
энергетических
уровней
в
соответствии
с
их
общими
угловыми
моментами
(
j
=l+
s
).
В
случае
ядра
,
состояния
с
параллельным
спариванием
и
большими
значениями
общего
углового
момента
являются
преимущественными
и
более
низкоэнергетическими
по
сравнению
с
обладателями
малыми
значениями
общего
спина
для
данной
комбинации
.
Упорядочение
энергетических
уровней
в
оболочечной
модели
спин
-
орбитального
/
гармонического
осциллятора
показано
на
Рис
. 9
совместно
с
их
спектроскопическими
обозначениями
.
Каждое
общее
состояние
углового
момента
имеет
2
j
+1
подоболочку
или
проекцию
углового
момента
(
m
j
=-j,…,0,…,+
j
) (
подобно
значениям
l
для
атомных
электронов
).
Заметим
,
что
мы
всегда
имеем
раздельные
состояния
для
нейтронов
и
протонов
,
и
принцип
Паули
относится
к
состояниям
двух
нейтронов
или
двух
протонов
на
каждой
орбите
.
Рассмотрим
расположение
нуклонов
в
этих
состояниях
оболочечной
модели
.
Наинизший
уровень
называется
1
s
1/2
,
s
для
J
=0,
и
j
=
J
+
s
=1/2.
Эти
уровни
имеют
только
2
l
+1=
m
значений
и
могут
разместить
только
два
протона
в
протоновой
яме
и
два
нейтрона
в
нейтроновой
яме
.
Следующие
уровни
:
пара
1
р
3/2
и
1
р
1/2
в
следующей
более
высокой
оболочке
(
N
=1
ħ
ω
).
4
He
представляет
собой
наименьшее
ядро
с
полным
заполнением
обеих
оболочек
N
=0
гармонического
оциллятора
для
нейтронов
и
протонов
и
,
как
можно
ожидать
,
это
ядро
будет
иметь
повышенную
стабильность
.
Заполнение
следующей
оболочки
происходит
,
когда
заполняются
оболочки
N
=0
ħ
ω
и
N
=1
ħ
ω
.
Это
требует
восемь
протонов
и
восемь
нейтронов
,
поэтому
16
О
должно
быть
особо
стабильным
ядром
.
Другие
полные
заполнения
оболочек
будут
происходить
при
20, 28,
50, 82
и
126
нуклонах
.
Эти
значения
соответствуют
нуклидам
,
имеющим
необычно
большое
число
изотопов
и
изотонов
ввиду
их
повышенной
стабильности
.
Несколько
стабильных
ядер
имеют
как
полностью
заполненные
нейтронные
и
протонные
оболочки
,
так
и
очень
сильные
связи
(
относительно
их
соседей
по
таблице
изотопов
).
К
ним
относятся
4
Не
,
16
О
,
40
Са
и
208
Pb.
Некоторые
ядра
с
обеими
заполненными
оболочками
,
находятся
за
пределами
стабильных
ядер
:
56
Ni,
100
Sn,
132
Sn,
10
Не
и
28
О
.
Отметим
,
что
лёгкие
ядра
чрезвычайно
«
хрупки
»
ввиду
большого
пространства
между
уровнями
и
относительно
малого
числа
уровней
.
Малое
число
нуклонов
весьма
чувствительно
к
малым
изменениям
в
конфигурациях
и
даёт
мало
возбуждённых
состояний
.
Тяжёлые
ядра
намного
более
«
упругие
»,
поскольку
имеют
большое
число
уровней
с
близкими
энергиями
несколько
различных
конфигураций
,
и
эти
ядра
почти
всегда
имеют
очень
большое
число
связанных
возбуждённых
состояний
.
Диаграмма
энергетических
уровней
,
построенная
в
рамках
оболочечной
модели
,
позволяет
предсказания
основных
состояниях
большого
числа
ядер
.
Сильное
спаривание
нуклонов
на
индивидуальных
орбитах
предсказывает
,
что
полный
спин
всего
ядра
с
чётным
числом
как
протонов
,
так
и
нейтронов
равен
нулю
.
Чётности
волновых
функций
всех
этих
ядер
положительны
.
Поэтому
спин
основного
состояния
и
чётность
всех
чётно
-
чётно
ядер
есть
0
+
.
Все
чётно
-
чётные
ядра
не
имеют
общего
ядерного
спина
,
и
поэтому
только
некоторые
ядра
используют
в
ЯМР
-
исследованиях
.
Основные
состояния
ядер
с
нечётным
А
,
с
чётным
числом
одного
вида
нуклонов
и
нечётным
числом
другого
вида
,
описываются
спином
и
чётностью
этого
единственного
нечётного
нуклона
.
Эти
предсказания
часто
являются
корректными
,
т
.
к
.
одиночная
вакансия
или
дырка
на
подоболочке
даёт
тот
же
угловой
момент
и
чётность
,
как
одиночная
частица
на
той
же
подоболочке
.
Однако
,
полностью
заполненная
подоболочка
имеет
спин
0,
поэтому
,
при
добавлении
одной
частицы
для
достижения
данного
значения
j
,
будет
тот
же
спина
,
что
и
при
удалении
одной
частицы
из
полностью
заполненной
подоболочки
.
Во
всех
возбуждённых
состояниях
ядро
может
находиться
лишь
конечное
время
,
до
тех
пор
,
пока
возбуждение
не
будет
снято
тем
или
иным
путём
.
Состояния
,
энергия
возбуждения
которых
меньше
энергии
связи
частицы
или
группы
частиц
в
данном
ядре
,
называются
связанными
,
в
этом
случае
возбуждение
может
сниматься
лишь
гамма
-
излучением
.
Состояния
с
энергией
возбуждения
,
превышающей
энергию
связи
частиц
,
называются
квазистационарными
.
В
этом
случае
ядро
может
испустить
частицу
или
гамма
-
квант
.
Рис
. 10.
Потенциальные
ямы
для
протонов
и
нейтронов
в
атомном
ядре
.
Поскольку
ядерные
силы
-
силы
короткодействующие
,
зависимость
потенциала
самосогласованного
поля
от
расстояния
до
центра
ядра
подобна
зависимости
от
радиуса
плотности
распределения
ядерной
материи
.
Кроме
того
,
потенциал
должен
быть
потенциалом
притяжения
.
В
модели
оболочек
предполагается
,
что
нуклоны
движутся
независимо
друг
от
друга
в
сферически
-
симметричной
потенциальной
яме
,
созданной
силами
всех
других
нуклонов
.
В
первом
приближении
потенциал
пропорционален
ядерной
плотности
и
,
следовательно
,
может
быть
описан
потенциалом
Вудса
-
Саксона
⎟
⎠
⎞
⎜
⎝
⎛ −
+
−
=
a
R
r
V
V
exp
1
0
(17)
где
грубые
оценки
параметров
:
V
0
≈
57
МэВ
,
R
≈
А
1/3
ферми
,
а
≈
0,65
ферми
.
Следует
ещё
учесть
спин
-
орбитальное
взаимодействие
(
Рис
. 10
).
Если
спин
-
противоположен
орбитальному
угловому
моменту
,
то
эффективная
потенциальная
яма
сужается
,
увеличивая
энергию
.
Это
видно
по
спин
-
орбитальном
расщеплению
уровней
(
Рис
. 11
).
Рис
. 11.
Заполнение
энергетических
уровней
ядра
нуклонами
.
Решение
для
гармонического
потенциала
в
квадратной
потенциальной
яме
даёт
серию
энергетических
уровней
.
Однако
обозначения
уровней
несколько
отличаются
от
соответствующих
символов
для
атомных
энергетических
уровней
.
Принцип
запрета
Паули
действует
в
случае
ядерных
частиц
точно
так
же
,
как
и
в
случае
электронов
,
но
в
модели
оболочек
он
приводит
к
тому
,
что
на
первой
оболочке
могут
находиться
только
два
протона
и
два
нейтрона
,
на
второй
–
по
шести
обеих
частиц
(
заполнена
у
16
О
)
и
на
третьей
по
десяти
(
заполнена
у
36
А
r).
Наличие
периодичности
в
структуре
ядер
проявляется
и
дальше
,
хотя
и
с
некоторыми
отступлениями
.
Энергетические
уровни
ядра
увеличиваются
с
ростом
квантового
числа
,
ответственного
за
орбитальный
угловой
момент
,
l,
s
,
p
,
d
,
f
...
символы
используется
для
l
=0,1,2,3 ...
точно
так
же
как
в
случае
атома
.
Но
в
оболочках
ядра
нет
никакого
физического
аналога
основному
квантовому
числу
n,
поэтому
числа
,
связанные
с
уровнем
,
только
начинаются
при
n
=1
для
самого
низкого
уровня
,
связанного
с
данным
орбитальным
квантовым
числом
,
давая
такой
символ
как
1
g
,
который
не
мог
возникнуть
в
атомной
схеме
обозначений
.
Квантовое
число
для
орбитального
углового
момента
не
оканчивается
n
,
как
в
случае
атома
.
Значительное
спин
-
орбитальное
взаимодействие
расщепляет
уровни
на
подуровни
,
число
которых
увеличивается
с
орбитальным
квантовым
числом
.
Это
приводит
к
наложению
уровней
(
Рис
.19).
Вклад
протона
в
энергию
ядра
несколько
отличается
от
вклада
нейтрона
из
-
за
кулоновского
отталкивания
,
но
это
даёт
небольшое
различие
в
наборе
энергетических
уровней
.
Суммарный
момент
системы
одинаковых
нуклонов
,
заполняющих
любую
подоболочку
,
равен
0
независимо
от
квантовых
чисел
подоболочки
и
числа
(2
j
+1)
заполняющих
её
нуклонов
(
нейтронов
или
протонов
).
Это
важное
правило
является
следствием
того
факта
,
что
среди
заполняющих
подоболочку
(2
j
+1)
одинаковых
нуклонов
будут
обязательно
находиться
нуклоны
с
равными
по
абсолютной
величине
,
но
разными
по
знаку
проекциями
полного
момента
нуклона
на
выделенную
ось
.
Такие
пары
одинаковых
нуклонов
имеют
суммарный
полный
момент
,
равный
0.
Поэтому
суммарные
моменты
как
нейтронов
,
так
и
протонов
на
заполненной
подоболочке
равны
0.
По
этой
причине
и
спины
основных
состояний
всех
ядер
с
заполненными
оболочками
или
подоболочками
равны
0.
Экспериментально
доказано
,
что
равны
нулю
спины
основных
состояний
всех
чётно
-
чётных
ядер
,
т
.
е
.
как
ядер
с
заполненными
подоболочками
или
оболочками
,
так
и
ядер
,
у
которых
на
подоболочке
находятся
по
чётному
числу
протонов
или
нейтронов
.
Объяснение
этого
экспериментального
факта
-
наличие
в
ядерных
взаимодействиях
не
учтенных
в
предыдущем
изложении
одночастичной
модели
оболочек
сил
-
т
.
н
.
сил
спаривания
.
Необходимо
отметить
,
что
замена
всех
действующих
между
нуклонами
сил
самосогласованным
потенциалом
со
спин
-
орбитальным
членом
является
довольно
грубым
модельным
приближением
.
Не
учтённые
силы
называются
силами
остаточного
взаимодействия
и
играют
важную
роль
в
формировании
свойств
ядер
.
Важнейшим
компонентом
сил
остаточного
взаимодействия
являются
силы
спаривания
.
Действие
сил
спаривания
приводит
к
тому
,
что
для
любых
двух
одинаковых
нуклонов
наиболее
выгодным
по
энергии
(
т
.
е
.
низшим
)
состоянием
будет
состояние
с
полным
моментом
0
или
,
иначе
говоря
,
с
противоположными
направлениями
проекций
полного
момента
на
выделенную
ось
.
Для
всех
чётных
по
Z
и
по
N
ядер
это
приводит
к
значениям
спина
0
в
основном
состоянии
.
Пространственная
четность
основных
состояний
всех
чётно
-
чётных
ядер
положительна
.
Спин
и
чётность
основного
состояния
ядра
с
одним
нуклоном
сверх
замкнутой
оболочки
или
подоболочки
определяется
моментом
и
чётностью
неспаренного
нуклона
.
Чётность
состояния
определяется
произведением
внутренних
чётностей
составляющих
его
частиц
на