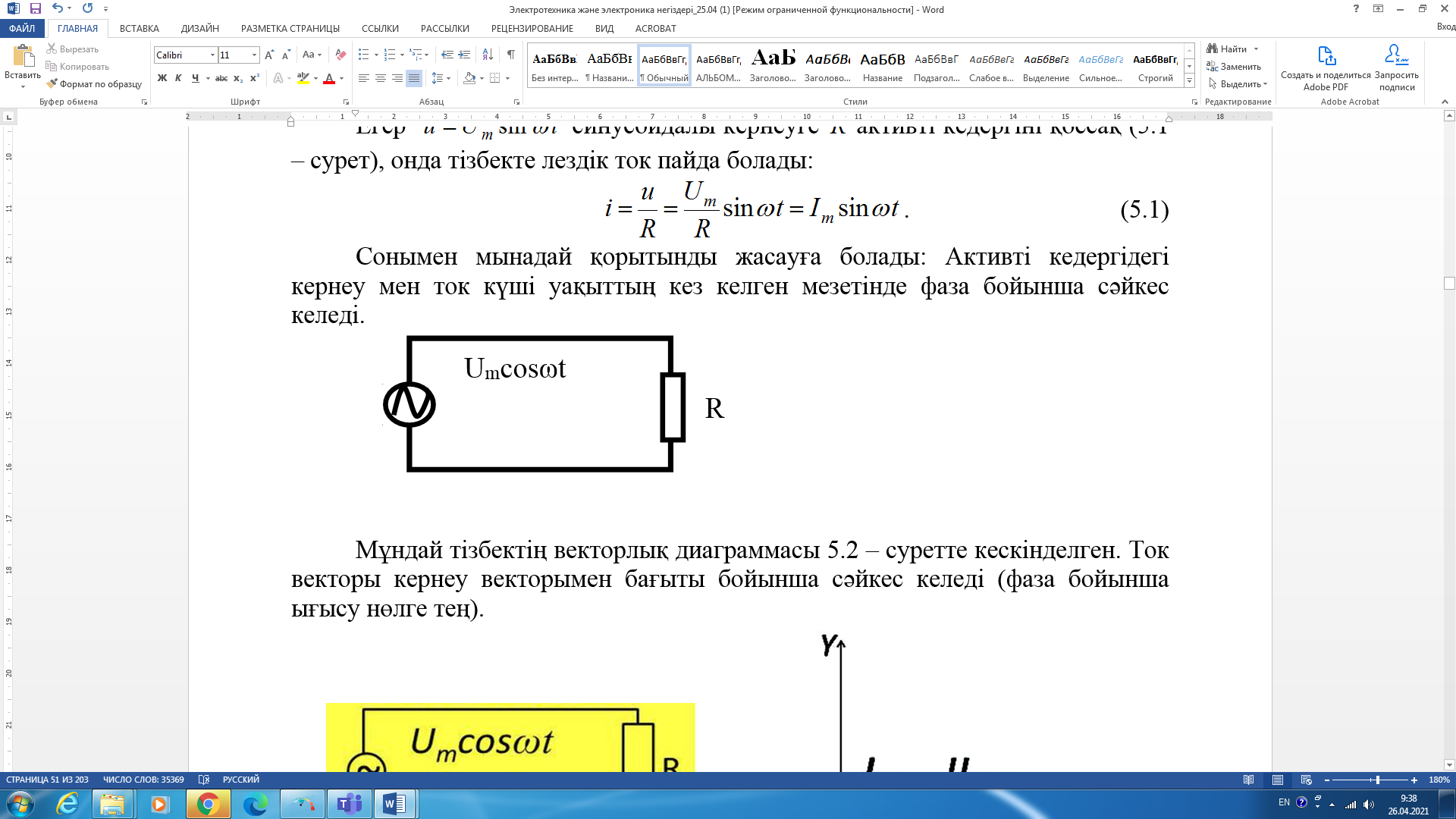
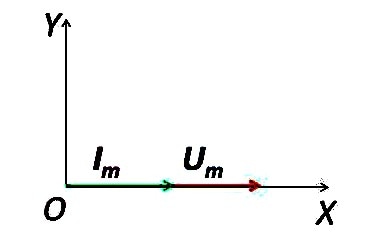
2.5.1 – сурет. Синусоидалы кернеуге резисторлы элементті қосу сұлбасы

2.5.2 – сурет. Активті кедергісі бар айнымалы ток тізбегінің векторлық диаграммасы

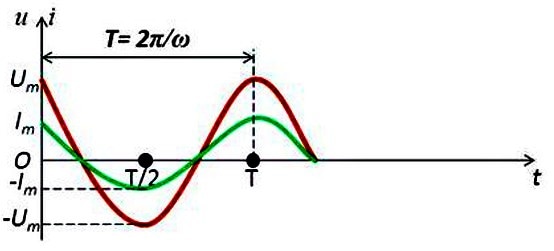
2.5.3 – сурет. Активті кедергісі бар айнымалы ток тізбегіндегі кернеу мен ток амплитудаларының уақытқа тәуелділік графигі
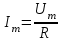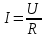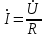, , . (2.5.2)

Бұл формула тізбек үшін Ом заңының амплитудалық мәнінің, әсерлі мәнінің және комплексті түрдегі жазылулары.
Индуктивті кедергісі бар айнымалы ток тізбегі және оның векторлық диаграммасы

Егер индуктивті элементі бар тізбекте 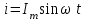синусоидалы ток өтетін болса (2.5.4-сурет) , онда өздік индукцияның ЭҚК-і

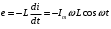. (2.5.3)

Кирхгофтың ІІ-заңы бойынша 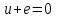, мұндағы кернеуді мына қатынаспен жазуға болады

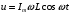немесе 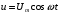, (2.5.4)

мұндағы .

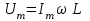Сонымен мынадай қорытынды жасауға болады: Индуктивтілік катушкадағы ток күшінің тербелісі фаза бойынша кернеу тербелісінен 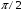-ге артта қалады.

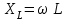(2.5.5)

шамасының өлшем бірлігі кедергінікіндей және индуктивті кедергі деп аталады. Индуктивті кедергіні реактивті кедергі деп атайды. Комплексті индуктивті кедергі мына қатынаспен анықталады

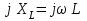. (2.5.6)

Бұл тізбектің векторлық диаграммасы 2.5.5 - суретте келтірілген. Кернеу векторы ток векторынан 90

---

⁰ – қа озып кетеді ( 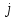символы ток векторын периодтың төрттен біріне сағат тіліне қарама-қарсы бұру қажет екенін көрсетеді). Индуктивті кедергісі бар айнымалы ток тізбегіндегі кернеу мен ток амплитудаларының уақытқа тәуелділік графигі 2.5.6 – суретте кескінделген.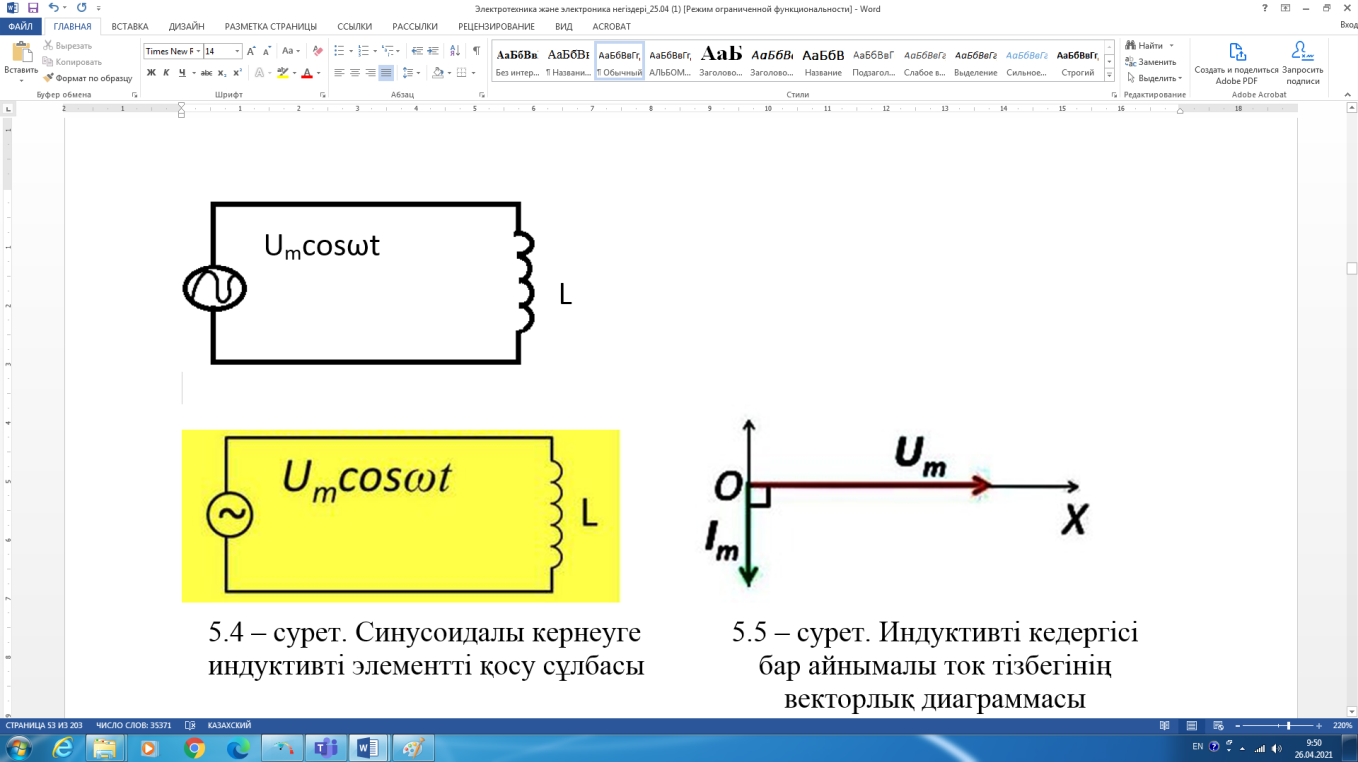

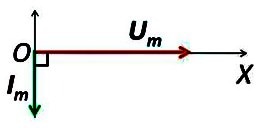
2.5.4 – сурет. Синусоидалы кернеуге индуктивті элементті қосу сұлбасы

2.5.5 – сурет. Индуктивті кедергісі бар айнымалы ток тізбегінің векторлық диаграммасы

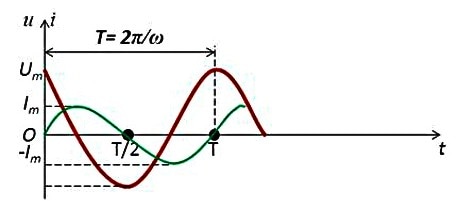
2.5.6 – сурет. Индуктивті кедергісі бар айнымалы ток тізбегіндегі кернеу мен ток амплитудаларының уақытқа тәуелділік графигі
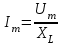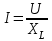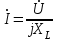, , . (2.5.7)

Индуктивті элементі бар тізбек үшін Ом заңының амплитудалық мәнінің, әсерлі мәнінің және комплексті түрдегі жазылулары.
Сыйымдылықты кедергісі бар айнымалы ток тізбегі

Егер синусоидалы ток тізбегінде идеаль сыйымдылықты элемент болса (2.5.7-сурет), онда ток мына заңмен өзгереді

. (2.5.8)

Егер , онда 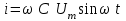немесе ,

мұндағы 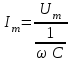. Сонымен мынадай қорытынды жасауға болады: Конденсатор арқылы өтетін ток күші ондағы кернеуден -ге озып кетеді.

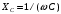шамасының өлшем бірлігі кедергінікіндей және сыйымдылықты кедергі деп аталады. Сыйымдылықты кедергі индуктивті кедергі сияқты реактивті кедергі болып табылады. Индуктивті кедергі ток пен индуктивті элементтің жиілігінің жоғарылауымен бірге өседі. Тұрақты ток тізбегіндегі индуктивтілікте реактивті кедергі болмайды.

---

. (2.5.9)

Тұрақты токтағы сыйымдылықты кедергі шексіздікке тең және айнымалы ток пен сыйымдылық элемент жиілігінің жоғарылауымен кемиді.

Комплексті сыйымдылықты кедергі мына қатынаспен анықталады

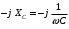. (2.5.10)

Тізбектің векторлық диаграммасы 2.5.8-суретте келтірілген. Ток векторының 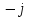- ға көбейтіндісі осы вектордың 90⁰ – қа сағат тілінің бағытымен бұрылуын көрсетеді. Сыйымдылықты кедергісі бар айнымалы ток тізбегіндегі кернеу мен ток амплитудаларының уақытқа тәуелділік графигі 2.5.9 – суретте көрсетілген.

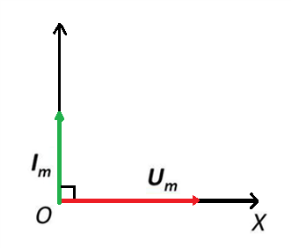
2.5.7 – сурет. Синусоидалы кернеуге индуктивті элементті қосу сұлбасы

2.5.8 – сурет. Индуктивті кедергісі бар айнымалы ток тізбегінің векторлық диаграммасы

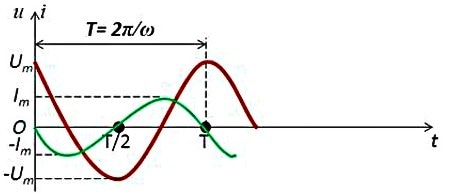ө

2.5.9 – сурет. Сыйымдылықты кедергісі бар айнымалы ток тізбегіндегі кернеу мен ток амплитудаларының уақытқа тәуелділік графигі

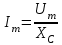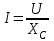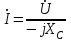, , . (2.5.11)

Бұл формула сыйымдылықты элементі бар тізбек үшін Ом заңының амплитудалық мәнінің, әсерлі мәнінің және комплексті түрдегі жазылулары.

Айнымалы токтың тармақталмаған тізбектері

Элементтерді тізбектей қосқан кезде (2.5.10-сурет) кернеудің лездік және комплексті мәндері мына қатынастармен жазылады

,

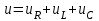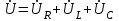. (2.5.12)

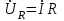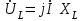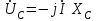, , болғандықтан векторлық диаграмма 2.5.11-суретте көрсетілген түрдегідей болады.

---

2.5.10-сурет. Катушка, резистор, конденсаторды тізбектей қосу сұлбасы

2.5.11-сурет. Тармақталмаған тізбектің векторлық диаграммасы

Векторлық диаграммадан кернеудің комплексті түрдегі өрнегін жазуға болады:

,

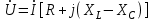немесе 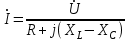. (2.5.13)

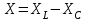айырымы реактивті кедергі деп аталады, оның комплексті түрі .

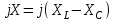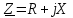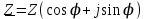; ; (2.5.14)

өрнектерін комплексті түрдегі толық кедергі деп атайды. Толық кедергінің модулін былай өрнектеуге болады:

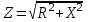, (2.5.15)

ал ток пен кернеу арасындағы бұрыш – 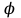мына қатынастан анықталады:

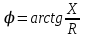. (2.5.16)

Векторлық диаграммадағы тікбұрышты үшбұрышты кедергілер үшбұрышына түрлендіруге болады (2.5.12-сурет). Кедергілер үшбұрышынан мынадай қатынастар шығады:

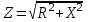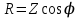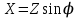, , , (2.5.17)

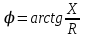немесе 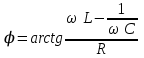. (2.5.18)

Фазалық ығысу оң деп есептеледі, егер .


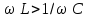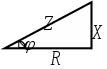
2.5.12-сурет. Кедергілер үшбұрышы: 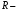активті кедергі; 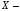реактивті кедергі; 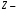толық кедергі,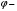

---

ток пен кернеу арасындағы бұрыш
Тармақталмаған тізбек үшін Ом заңы үшін әсерлі мәндері және комплексті түрдегі жазылуы:

, ,

, .

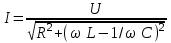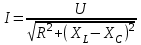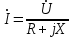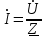, . (2.5.19)

Тармақталмаған тізбекті тұрақты токтың тізбегі сияқты символдық әдіспен есептеуге болады. 2.5.13-суреттегі тізбекті есептеу үшін толық кедергіні анықтау қажет, яғни мына қатынасты жазуға болады:

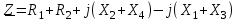. (2.5.20)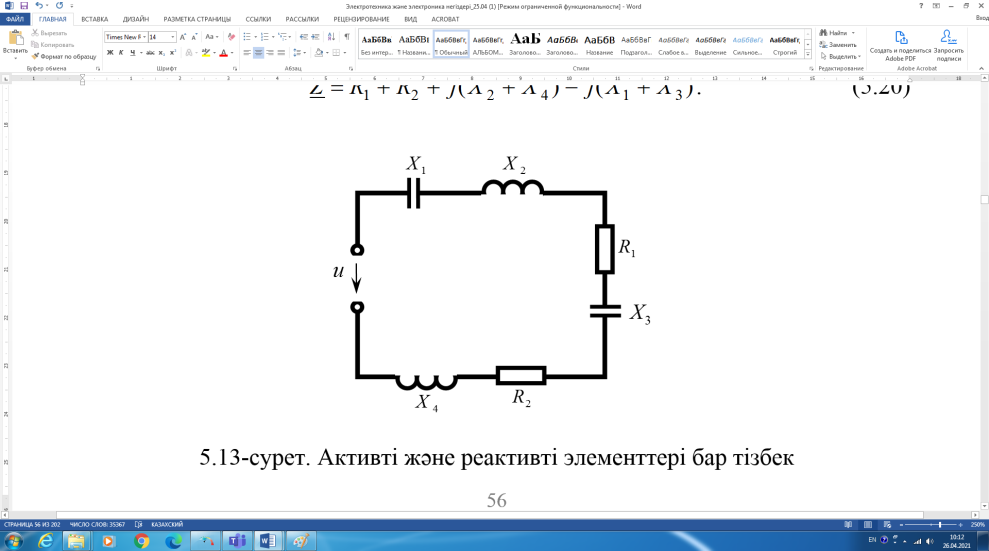


2.5.13-сурет. Активті және реактивті элементтері бар тізбек
Сонымен барлық индуктивті кедергі « 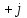» символына көбейтіледі, ал барлық сыйымдылықты кедергі « » символына көбейтіледі. Егер 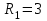, , 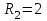, , 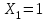, , 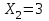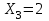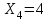онда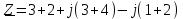



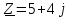. (2.5.21)

Осыдан шығатын қорытынды: барлық тізбекті эквивалентті кедергімен ауыстыруға болады. Бұл кедергі нақты (активті кедергі 5 Ом) және жорамал (индуктивті реактивті кедергі 4 Ом) бөліктерден тұрады.


Айнымалы токтың тармақталған тізбектері

Элементтерді параллель қосқан кезде (2.5.14-сурет) токтың лездік мәні мен оның комплексті түрі Кирхгофтың І–заңы бойынша мына қатынастармен жазылады

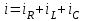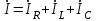, . (2.5.22)

---

Смотрите также файлы

• Комплексная механизация возделывания и уборки озимой пшеницы в условиях хозяйства.docx

• німдерді тасымалдауда заымданудан орау масатында ыдыстарды тыындау ралдарын дайындау, орау, тыыз тсеу амортизациялауа олданылатын материал.docx

• Главными задачами курсовой работы являются.docx

• Деловая репутация организации как объект учета.docx

• Методом изоклин построить интегральные кривые уравнения Если принять.docx