ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 84
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
активті өткізгіштік, 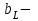 реактивті индуктивтілік өткізгіштік,
реактивті индуктивтілік өткізгіштік, 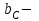 реактивті сыйымдылық өткізгіштік арқылы символдық түрі былай жазылады:
реактивті сыйымдылық өткізгіштік арқылы символдық түрі былай жазылады:
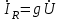 ,
, 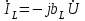 ,
, 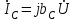 . (2.5.23)
. (2.5.23)
Кирхгофтың І–заңына сәйкес векторлық диаграммасы 2.5.15-суреттегідей болады.

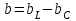 айырымын реактивті өткізгіштік деп атайды. Бұл жағдайда толық өткізгіштікті комплексті түрде былай анықтауға болады:
айырымын реактивті өткізгіштік деп атайды. Бұл жағдайда толық өткізгіштікті комплексті түрде былай анықтауға болады:
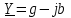 ;
; 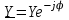 ;
; 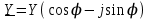 , (2.5.24)
, (2.5.24)
мұндағы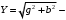 толық өткізгіштіктің модулі, ал
толық өткізгіштіктің модулі, ал 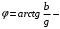 ток пен кернеу арасындағы фазалық ығысу.
ток пен кернеу арасындағы фазалық ығысу.
Векторлық диаграмманың тікбұрышты үшбұрышын өткізгіштіктер үшбұрышына түрлендіруге болады (2.5.16-сурет). Осы үшбұрыштан өткізгіштіктер арасындағы мынадай қатынастар шығады:
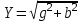 ,
, 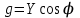 ,
, 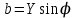 ,
, 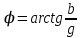 . (2.5.25)
. (2.5.25)
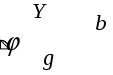
2.5.16-сурет. Өткізгіштіктер үшбұрышы: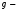 активті өткізгіштік;
активті өткізгіштік; 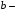 реактивті өткізгіштік;
реактивті өткізгіштік; 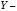 толық өткізгіштік,
толық өткізгіштік,  ток пен кернеу арасындағы бұрыш
ток пен кернеу арасындағы бұрыш
Векторлық диаграмманың тікбұрышты үшбұрышы сондай-ақ мына қатынасты береді:
 . (2.5.26)
. (2.5.26)
Бұл қатынас тармақталған тізбек үшін алгебралық түрдегі Ом заңы болып табылады. Ом заңы символдық түрде былай жазылады
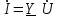 немесе
немесе 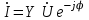 . (2.5.27)
. (2.5.27)
Толық кедергіні электр тізбегінің импедансы деп атайды. Активті кедергіні резистанс, реактивтіні – реактанс деп атайды. Реактанс индуктивті (индуктивті кедергі) және (сыйымдылықты кедергі) сыйымдылықты болады. Толық өткізгіштікті электр тізбегінің адмитансы деп атайды. Активті өткізгіштікті кондуктанс, реактивтіні – сусцептанс деп атайды. Сусцептанс индуктивті (индуктивті өткізгіштік) және (сыйымдылықты өткізгіштік) сыйымдылықты болады.
Кернеулер резонансы
Тармақталмаған тізбек (2.5.17-сурет) үшін Ом заңы мына түрде болады.
 . (2.5.28)
. (2.5.28)
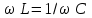 шарты орындалған жағдайда кернеулер резонансы құбылысы байқалады.
шарты орындалған жағдайда кернеулер резонансы құбылысы байқалады.
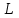 және
және 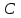 параметрлері өзгермейтін болса, резонанс шартын ток жиілігін өзгерту арқылы орындауға болады. Резонанстық жиілікті былай анықтайды:
параметрлері өзгермейтін болса, резонанс шартын ток жиілігін өзгерту арқылы орындауға болады. Резонанстық жиілікті былай анықтайды:
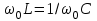 ,
, 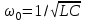 . (2.5.29)
. (2.5.29)
Резонанс жағдайында индуктивтілік пен сыйымдылықтағы кернеу тең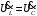 . Мұндай жағдайдың тізбек сұлбасы 2.5.17-суретте, ал векторлық диаграммасы 2.5.18-суретте келтірілген.
. Мұндай жағдайдың тізбек сұлбасы 2.5.17-суретте, ал векторлық диаграммасы 2.5.18-суретте келтірілген.

Резонанс кезінде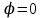 ,
, 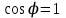 ,
, 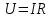
,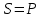 .
.
Егер активті кедергі аз, яғни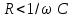 және
және 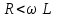 болса, онда желідегі кернеуден анағұрлым артық болатын едәуір ток және сыйымдылық пен индуктивтілікте үлкен кернеу пайда болады.
болса, онда желідегі кернеуден анағұрлым артық болатын едәуір ток және сыйымдылық пен индуктивтілікте үлкен кернеу пайда болады.
Резонансты жиілік кезінде реактивті кедергі шамасын толқындық кедергі (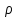 ) деп атайды
) деп атайды  ;
; 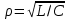 . (2.5.30)
. (2.5.30)
Контурдың төзімділігі (добротность) деп толқындық кедергінің активті кедергіге қатынасын айтады, яғни . (2.5.31)
. (2.5.31)
Төзімділік реактивті элементтердегі кернеу резистивті элементтердегі кернеуден неше есе асып түсетінін анықтайды.
 ,
, 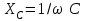 ,
,  екенін ескере отырып, жиіліктік сипаттамаларды тұрғызуға болады. (2.5.19-сурет) Резонанстық қисықтар
екенін ескере отырып, жиіліктік сипаттамаларды тұрғызуға болады. (2.5.19-сурет) Резонанстық қисықтар 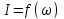 және
және 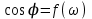 тәуелділіктері 2.5.20-суретте келтірілген.
тәуелділіктері 2.5.20-суретте келтірілген.
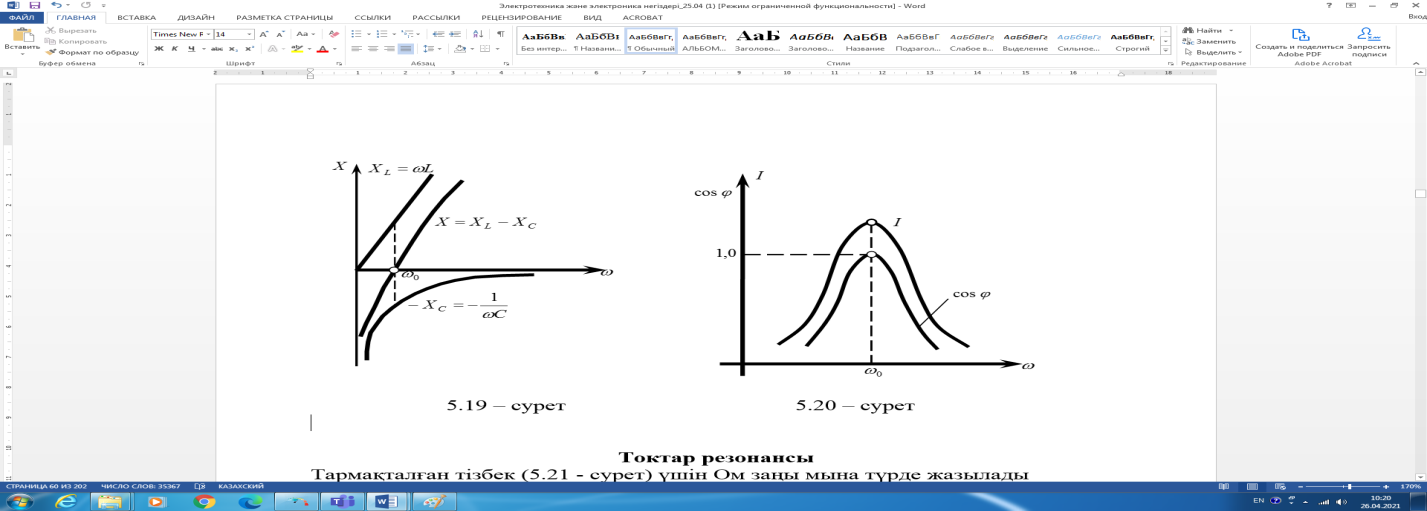
2.5.19 – сурет. Жиілік сипаттамалары 2.5.20 – сурет. Резонанс қисықтары
Резонанс кезінде тізбектегі ток ең үлкен мәніне жетеді, ал қуат коэффициенті 1–ге тең.
Токтар резонансы
Тармақталған тізбек 2.5.21 - сурет үшін Ом заңы мына түрде жазылады
 . (2.5.32)
. (2.5.32)
Егер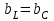 болса, онда токтар резонансы құбылысы орын алады. Бұл жағдайда реактивті элементтері бар тармақтардағы токтар тең және қарама-қарсы бағытталған, векторлық диаграммасы 2.5.22-суретте келтірілген. Реактивті элементтері бар тармақтардағы токтар тізбектің тармақталмаған бөлігіндегі токтан едәуір артығырақ болуы мүмкін.
болса, онда токтар резонансы құбылысы орын алады. Бұл жағдайда реактивті элементтері бар тармақтардағы токтар тең және қарама-қарсы бағытталған, векторлық диаграммасы 2.5.22-суретте келтірілген. Реактивті элементтері бар тармақтардағы токтар тізбектің тармақталмаған бөлігіндегі токтан едәуір артығырақ болуы мүмкін.
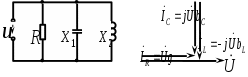
2.5.21 – сурет. Тармақталған тізбек 2.5.22 – сурет. Векторлық диаграмма
Кернеулер резонансындағы сияқты токтар резонансында да мына қатынастар орын алады:
 ,
,  ,
,  ,
,  .
.
Токтар резонансы кезінде тізбектің толқындық өткізгіштігі (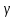 ) түсінігі қолданылады
) түсінігі қолданылады
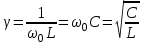 . (2.5.33)
. (2.5.33)
Бұл жағдайдағы тізбектің төзімділігі
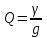 , (2.5.34)
, (2.5.34)
және реактивті элементтері бар тармақтардағы токтар тізбектің тармақталмаған бөлігіндегі токтан неше есе артық екенін көрсетеді.
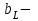 реактивті индуктивтілік өткізгіштік,
реактивті индуктивтілік өткізгіштік, 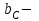 реактивті сыйымдылық өткізгіштік арқылы символдық түрі былай жазылады:
реактивті сыйымдылық өткізгіштік арқылы символдық түрі былай жазылады: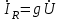 ,
, 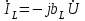 ,
, 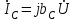 . (2.5.23)
. (2.5.23)Кирхгофтың І–заңына сәйкес векторлық диаграммасы 2.5.15-суреттегідей болады.

| 2.5.14-сурет. Катушка, резистор, конденсаторды параллель қосу сұлбасы | 2.5.15-сурет. Тармақталған тізбектің векторлық диаграммасы |
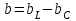 айырымын реактивті өткізгіштік деп атайды. Бұл жағдайда толық өткізгіштікті комплексті түрде былай анықтауға болады:
айырымын реактивті өткізгіштік деп атайды. Бұл жағдайда толық өткізгіштікті комплексті түрде былай анықтауға болады: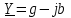 ;
; 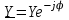 ;
; 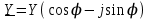 , (2.5.24)
, (2.5.24)мұндағы
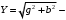 толық өткізгіштіктің модулі, ал
толық өткізгіштіктің модулі, ал 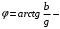 ток пен кернеу арасындағы фазалық ығысу.
ток пен кернеу арасындағы фазалық ығысу.Векторлық диаграмманың тікбұрышты үшбұрышын өткізгіштіктер үшбұрышына түрлендіруге болады (2.5.16-сурет). Осы үшбұрыштан өткізгіштіктер арасындағы мынадай қатынастар шығады:
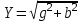 ,
, 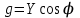 ,
, 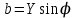 ,
, 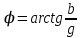 . (2.5.25)
. (2.5.25)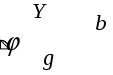
2.5.16-сурет. Өткізгіштіктер үшбұрышы:
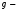 активті өткізгіштік;
активті өткізгіштік; 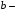 реактивті өткізгіштік;
реактивті өткізгіштік; 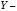 толық өткізгіштік,
толық өткізгіштік,  ток пен кернеу арасындағы бұрыш
ток пен кернеу арасындағы бұрышВекторлық диаграмманың тікбұрышты үшбұрышы сондай-ақ мына қатынасты береді:
 . (2.5.26)
. (2.5.26)Бұл қатынас тармақталған тізбек үшін алгебралық түрдегі Ом заңы болып табылады. Ом заңы символдық түрде былай жазылады
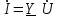 немесе
немесе 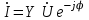 . (2.5.27)
. (2.5.27)Толық кедергіні электр тізбегінің импедансы деп атайды. Активті кедергіні резистанс, реактивтіні – реактанс деп атайды. Реактанс индуктивті (индуктивті кедергі) және (сыйымдылықты кедергі) сыйымдылықты болады. Толық өткізгіштікті электр тізбегінің адмитансы деп атайды. Активті өткізгіштікті кондуктанс, реактивтіні – сусцептанс деп атайды. Сусцептанс индуктивті (индуктивті өткізгіштік) және (сыйымдылықты өткізгіштік) сыйымдылықты болады.
Кернеулер резонансы
Тармақталмаған тізбек (2.5.17-сурет) үшін Ом заңы мына түрде болады.
 . (2.5.28)
. (2.5.28)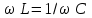 шарты орындалған жағдайда кернеулер резонансы құбылысы байқалады.
шарты орындалған жағдайда кернеулер резонансы құбылысы байқалады.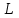 және
және 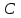 параметрлері өзгермейтін болса, резонанс шартын ток жиілігін өзгерту арқылы орындауға болады. Резонанстық жиілікті былай анықтайды:
параметрлері өзгермейтін болса, резонанс шартын ток жиілігін өзгерту арқылы орындауға болады. Резонанстық жиілікті былай анықтайды: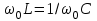 ,
, 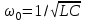 . (2.5.29)
. (2.5.29)Резонанс жағдайында индуктивтілік пен сыйымдылықтағы кернеу тең
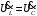 . Мұндай жағдайдың тізбек сұлбасы 2.5.17-суретте, ал векторлық диаграммасы 2.5.18-суретте келтірілген.
. Мұндай жағдайдың тізбек сұлбасы 2.5.17-суретте, ал векторлық диаграммасы 2.5.18-суретте келтірілген. 
| .5.17-сурет. Тармақталмаған тізбек сұлбасы | 2.5.18-сурет. Резонанс жағдайындағы 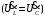 тармақталмаған тізбектің векторлық диаграммасы тармақталмаған тізбектің векторлық диаграммасы |
Резонанс кезінде
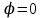 ,
, 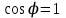 ,
, 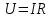
,
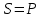 .
.Егер активті кедергі аз, яғни
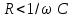 және
және 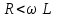 болса, онда желідегі кернеуден анағұрлым артық болатын едәуір ток және сыйымдылық пен индуктивтілікте үлкен кернеу пайда болады.
болса, онда желідегі кернеуден анағұрлым артық болатын едәуір ток және сыйымдылық пен индуктивтілікте үлкен кернеу пайда болады.Резонансты жиілік кезінде реактивті кедергі шамасын толқындық кедергі (
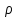 ) деп атайды
) деп атайды  ;
; 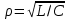 . (2.5.30)
. (2.5.30)Контурдың төзімділігі (добротность) деп толқындық кедергінің активті кедергіге қатынасын айтады, яғни
 . (2.5.31)
. (2.5.31)Төзімділік реактивті элементтердегі кернеу резистивті элементтердегі кернеуден неше есе асып түсетінін анықтайды.
 ,
, 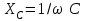 ,
,  екенін ескере отырып, жиіліктік сипаттамаларды тұрғызуға болады. (2.5.19-сурет) Резонанстық қисықтар
екенін ескере отырып, жиіліктік сипаттамаларды тұрғызуға болады. (2.5.19-сурет) Резонанстық қисықтар 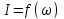 және
және 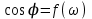 тәуелділіктері 2.5.20-суретте келтірілген.
тәуелділіктері 2.5.20-суретте келтірілген. 
2.5.19 – сурет. Жиілік сипаттамалары 2.5.20 – сурет. Резонанс қисықтары
Резонанс кезінде тізбектегі ток ең үлкен мәніне жетеді, ал қуат коэффициенті 1–ге тең.
Токтар резонансы
Тармақталған тізбек 2.5.21 - сурет үшін Ом заңы мына түрде жазылады
 . (2.5.32)
. (2.5.32)Егер
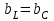 болса, онда токтар резонансы құбылысы орын алады. Бұл жағдайда реактивті элементтері бар тармақтардағы токтар тең және қарама-қарсы бағытталған, векторлық диаграммасы 2.5.22-суретте келтірілген. Реактивті элементтері бар тармақтардағы токтар тізбектің тармақталмаған бөлігіндегі токтан едәуір артығырақ болуы мүмкін.
болса, онда токтар резонансы құбылысы орын алады. Бұл жағдайда реактивті элементтері бар тармақтардағы токтар тең және қарама-қарсы бағытталған, векторлық диаграммасы 2.5.22-суретте келтірілген. Реактивті элементтері бар тармақтардағы токтар тізбектің тармақталмаған бөлігіндегі токтан едәуір артығырақ болуы мүмкін.
2.5.21 – сурет. Тармақталған тізбек 2.5.22 – сурет. Векторлық диаграмма
Кернеулер резонансындағы сияқты токтар резонансында да мына қатынастар орын алады:
 ,
,  ,
,  ,
,  .
.Токтар резонансы кезінде тізбектің толқындық өткізгіштігі (
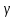 ) түсінігі қолданылады
) түсінігі қолданылады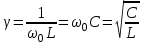 . (2.5.33)
. (2.5.33)Бұл жағдайдағы тізбектің төзімділігі
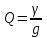 , (2.5.34)
, (2.5.34)және реактивті элементтері бар тармақтардағы токтар тізбектің тармақталмаған бөлігіндегі токтан неше есе артық екенін көрсетеді.