Файл: Контрольная работа 1 по Картографии название дисциплины студента заочного отделения фдфо специальности.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 116
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
«Московский государственный университет
геодезии и картографии»
ФАКУЛЬТЕТ ДИСТАНЦИОННЫХ ФОРМ ОБУЧЕНИЯ
ЗАОЧНОЕ ОТДЕЛЕНИЕ
КОНТРОЛЬНАЯ РАБОТА № 1
по __Картографии___
название дисциплины
студента заочного отделения ФДФО
специальности_____________
указать специальность обучения
_______________________________
Фамилия
________________________________
имя
________________________________
отчество
Шифр ХХ х-Х61 Вариант 61
Домашний адрес (индекс), мобильный телефон: _____________________________________________
1. ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
Контрольная работа предусматривает выполнение двух заданий:
1. Вычисление и построение картографической сетки нормальной равноугольной цилиндрической проекции (проекции Меркатора).
2. Решение картометрических задач на сетке проекции Меркатора.
Исходные данные для вычислений:
Номер Варианта 61
варианта Исходные
Таблица 1.
| Номер варианта | Исходные данные для задания №1 | Исходные данные для задания №2 | |
| 61 | 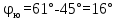 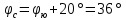 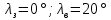 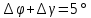 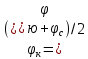 = (16+36)/2 = 26 = (16+36)/2 = 26 | Точка А | Точка В |
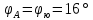  | 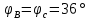 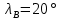 | ||
-
Вычисление параметра проекции β
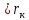 ,
,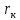 – радиус параллели (на земном эллипсоиде) с широтой
– радиус параллели (на земном эллипсоиде) с широтой 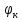 , который выбирается из картографических таблиц [см. приложение 2 ]. В данном случае φk =26, поэтому β =
, который выбирается из картографических таблиц [см. приложение 2 ]. В данном случае φk =26, поэтому β = 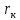 = 5736419 м или в масштабе карты:
= 5736419 м или в масштабе карты: 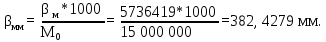
-
Вычисление абсциссы х, частных масштабов и искажений
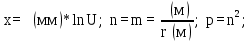
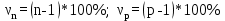
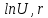 выбираются из картографических таблиц [см. приложение 2 ].
выбираются из картографических таблиц [см. приложение 2 ].Вычисления заносим в таблицу 2.
Таблица 2.
| φ | 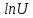 | х (мм) | 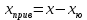 c | r(м) | n=m | 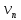 (%) | p | 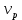 (%) |
| 16° | 0,2811093 | 107,504 | 0,00 | 6132722 | 0,935 | -6,46 | 0,875 | -12,51 |
| 21° | 0,3726127 | 142,497 | 34,99 | 5957166 | 0,963 | -3,71 | 0,927 | -7,27 |
| 26° | 0,4672772 | 178,700 | 71,20 | 5736419 | 1,000 | 0,00 | 1,000 | 0,00 |
| 31° | 0,5661133 | 216,498 | 108,99 | 5472083 | 1,048 | 4,83 | 1,099 | 9,89 |
| 36° | 0,6703382 | 256,356 | 148,85 | 5166085 | 1,110 | 11,04 | 1,233 | 23,30 |
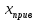 – вспомогательное значение абсциссы, по которой строится картографическая сетка
– вспомогательное значение абсциссы, по которой строится картографическая сетка-
Вычисление ординаты у
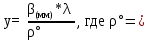 57,2957795°
57,2957795°Вычисления заносим в таблицу 3.
Таблица 3. – Ординаты y
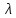 | 0° | 5° | 10° | 15° | 20° |
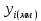 | 0 | 33,37 | 66,75 | 100,12 | 133,49 |
4. Построение картографической сетки
По вычисленным прямоугольным координатам
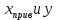 на миллимитровой бумаге необходимо построить сетку проекции Меркатора (Приложение 1)
на миллимитровой бумаге необходимо построить сетку проекции Меркатора (Приложение 1)2. ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
Номер Варианта 61
Таблица 4. - Исходные данные
| Номер варианта | Исходные данные для задания №1 | Исходные данные для задания №2 | |
| 61 |  = (16+36)/2 = 26 = (16+36)/2 = 26 R= 6365050 м. | Точка А | Точка В |
  |   | ||
-
Построение линий положения
1.1. Построение локсодромии
Проекция Меркатора обладает свойством локсодромичности, т.е. локсодромия в ней изображается прямой линией. Нанесем на сетку проекции Меркатора точки А и В по их географическим координатам. Соединив их прямой линией
, получим локсодромию (рис.3). Примечание.
-
Построение ортодромии
Чтобы построить ортодромию, необходимо вычислить географические координаты ее промежуточных точек. Для упрощения задачи можно вычислить координаты
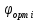 точек, лежащих на меридианах картографической сетки
точек, лежащих на меридианах картографической сетки 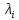 . С этой целью вначале вычисляется вспомогательный угол u:
. С этой целью вначале вычисляется вспомогательный угол u: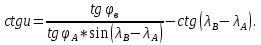
В данном примере:
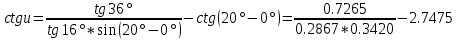 = 4.66187916
= 4.66187916 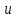 = 12, 106811°
= 12, 106811° Затем вычисляем широту точки пересечения ортодромии с заданным меридианом
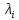 :
: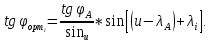
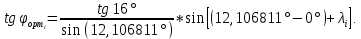
-
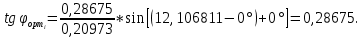 (16°)
(16°) -
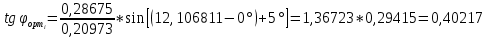 (21,9°)
(21,9°) -
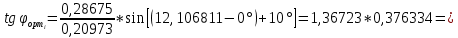 0,51453(27,2°)
0,51453(27,2°) -
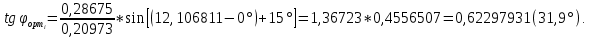
-
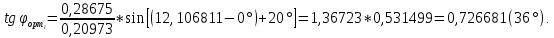
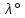 | 0 | 5 | 10 | 15 | 20 |
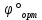 | 16,0 | 21,9 | 27,2 | 31,9 | 36,0 |
По географическим координатам наносим промежуточные точки ортодромии и, соединяя их по лекалу, строим линию ортодромии (рис.1)
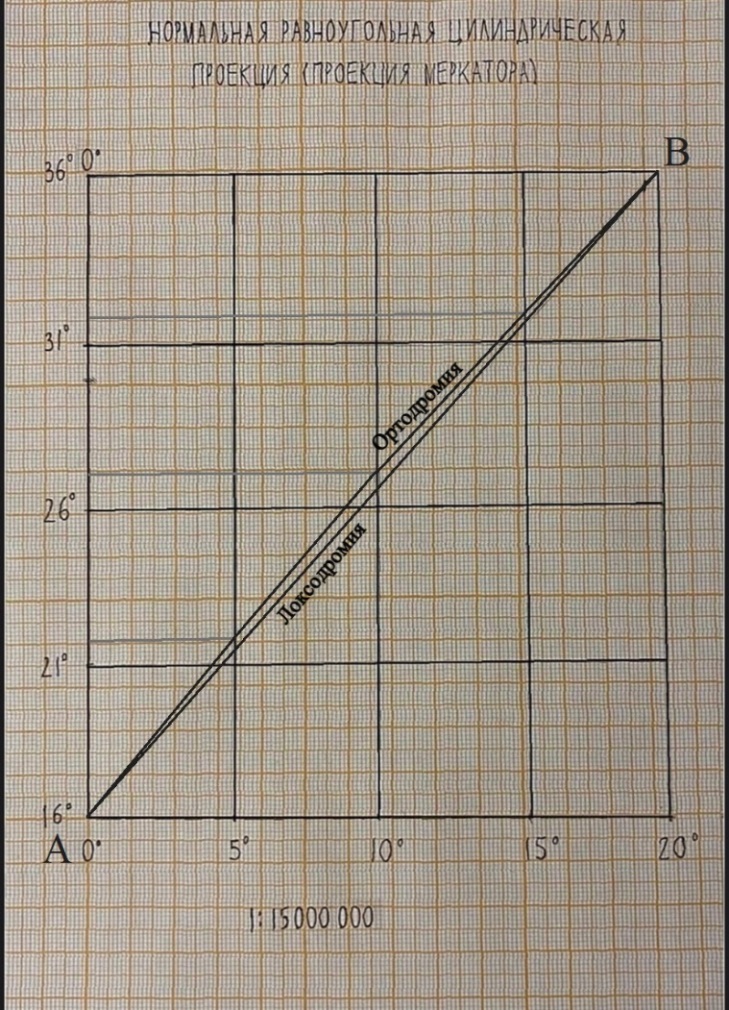
Рис. 1 – Построение локсодромии и ортодромии
-
Вычисление длин линий и площади участка по формулам
-
Вычисление длины ортодромии (на шаре)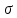
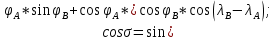
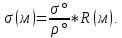
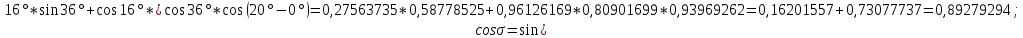
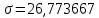 °;
°;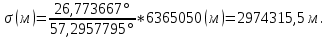
-
Вычисление длины локсодромии (на шаре) s
Сначала вычисляем азимут локсодромии αлокс:
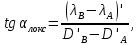
где D´ – меридианные части, которые выбираются из картографических таблиц [см. приложение] по широтам точек А и В
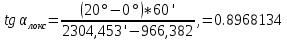
 = 41,886182°.
= 41,886182°.Длина локсодромии на шаре вычисляется по формуле:
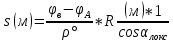
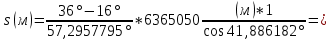
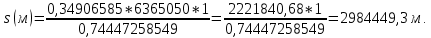
2.3. Вычисление площади участка P
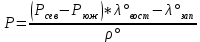
где P сев и P юж – площади трапеций протяжением от экватора до текущей параллели ( сев и юж) и разностью долгот в один радиан [см. приложение].
В данном случае:
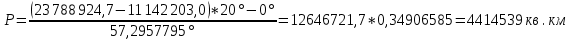 .
. -
Измерение длины локсодромии и площади участка
В проекции Меркатора частные масштабы длин и площадей зависят от широты, поэтому при измерении длин и площадей необходимо учитывать изменение частных масштабов. Для этого измеряемые отрезки и площади разделяют на части, в пределах которых величины частных масштабов принимают постоянными.