Добавлен: 26.10.2023
Просмотров: 129
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Приложение 10
Внеклассное мероприятие по математике для 8 классов, направленное на развитие критического мышления
Мероприятие проводится в виде соревнования между учащимися 8-го класса, которых делят на две или более команды.
Командам предлагаются задания и даётся время на обсуждение.
Затем игроки представляют решение своей команды. За правильные ответы выставляются соответствующие баллы.
1. Командам предлагается четыре задачи:
Задача 1.
В полдень из Москвы в Тулу выходит автобус с пассажирами. Часом позже из Тулы в Москву выезжает велосипедист и едет по тому же шоссе, но, конечно, значительно медленнее, чем автобус. Когда пассажиры автобуса и велосипедист встретятся, то кто из них будет дальше от Москвы? (1 балл)
Задача 2. Что дороже: килограмм гривенников или полкилограмма двугривенных? (1 балл)
Задача 3.
Если в 12 часов дня идёт дождь, то можно ли ожидать, что через 36 часов будет солнечная погода? (1 балл)
Задача 4 (шутка).
Недалеко от берега стоит корабль со спущенной на воду веревочной лестницей вдоль борта. У лестницы 10 ступенек. Расстояние между ступеньками 30 см. Самая нижняя ступенька касается поверхности воды. Океан сегодня очень спокоен, но начинается прилив, который поднимает воду за каждый час на 15 см.Через сколько часов покроется водой третья ступенька веревочной лесенки? (1 балл)
2. Командам предлагается решить следующую задачу:
10 цыплят в 10 дней съедают 1 кг зерна. Сколько килограммов зерна съедят 100 цыплят за 100 дней? (1 балл)
3. Учащимся раздаются спички и предлагается выложить из них такое «равенство»:

Как видно, равенство неверное. Нужно:
А) Переложите одну спичку так, чтобы получилось правильное равенство. (1 балл)
Б) Переложите две спички так, чтобы равенство осталось верным. (1 балл)
4. ИЗ ТРЕХ- ЧЕТЫРЕ (шутка)
На столе лежат 3 спички. Не прибавляя ни одной спички, необходимо сделать из трех — четыре. Ломать спички нельзя. (1 балл)
5. ТРИ ДА ДВА - ВОСЕМЬ ( шутка)
На столе лежат 3 спички. Нужно добавить к ним еще 2 так, чтобы получилось восемь. Разумеется, ломать спички нельзя. (1 балл)
7. Учащимся демонстрируются следующие рисунки:

И предлагается определить на глаз, какой из отрезков длиннее (верхний или нижний, длина или ширина, верхняя часть или нижняя, вертикальный или горизонтальный). (по 0,5 балла за каждую пару отрезков)
Скорее всего, учащиеся допустят ошибки. Тогда им даётся возможность с помощью измерений убедиться, что все отрезки попарно равны.
После этого уже вне конкурса разбираются следующие примеры того, как наблюдение над чертежом может привести нас к грубо ошибочным выводам:
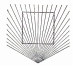
Фигура, изображённая на этом рисунке не трапеция, как кажется на первый взгляд, а квадрат.
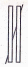
Линия, расположенная за двумя параллельными полосками прямая, а не ломаная.

Заштрихованные прямые параллельны.
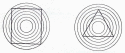
Стороны этих фигур не кривые. На самом деле это прямоугольник и треугольник.
Затем обсуждаем рис. 7 и выясняем, что на этом рисунке можно увидеть два кубика сверху и один снизу и наоборот. Всё зависит от того, как падает свет, когда мы смотрим на рисунок.
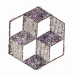
Из всех этих наблюдений, мы делаем вывод о том, что нельзя доверять своим глазам. И при решении задач нельзя руководствоваться только чертежом, необходимо обосновывать всё, чем мы пользуемся в ходе решения.
8 и 9. Работа с софизмами.
Учащимся предлагается найти ошибку в рассуждениях, приводящих к следующим утверждениям: прямой угол равен тупому и все числа равны между собой.
Предполагается, что ранее учащиеся уже встречались с математическими софизмами и имеют некоторый опыт работы с ними.
8. Прямой угол равен тупому. (3 балла)
Построим четырехугольник АВСD (рис. 8), у которого угол DАВ прямой, а стороны АD и BС равны. Очевидно, что угол АВС тупой.
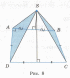
Из середин сторон АВ и DС восстановим перпендикуляры, которые пересекутся в некоторой точке S. Соединим эту точку S со всеми вершинами четырехугольника АВСD.
Рассмотрим образовавшиеся треугольники ASO и BSO, они равны по двум катетам. Поскольку в равных треугольниках соответствующие углы тоже равны, то угол АSO = углу ВSO.(1)
Рассмотрим треугольники SDF и SCF,они равны по двум катетам. Следовательно, сторона SD равна стороне SC.
Теперь рассмотрим треугольники АSD и ВSС. У них стороны АS и BS равны, т.к. треугольник АSO равен треугольнику ВSO. Стороны SD и SC равны, т. к. треугольники SDF и SCF равны. Стороны AD и BC равны по построению. Следовательно, треугольники ASD и SВС равны по трем сторонам. Поскольку в равных треугольниках соответствующие углы тоже равны, то угол SАD = углу SВС (2)
Вычитая равенство (1) из равенства (2), получим, что
угол SAD - угол SAB = угол SBC - угол SBA.
Поскольку угол SAD - угол SAB = углу DAB, а угол S BC - угол SBA = углу ABC,
получим, что угол DAB = углу ABC,
т. е. прямой угол равен тупому.
9. Все числа равны между собой. (3 балла)
Пусть a и bдва произвольных различных числа: a≠b. И пусть a – b = c.
Тогда a = b + c.Умножая обе части последнего равенства на a - b, получим:
a (a - b) = (b + c)(a - b);
a²- аb = bа + са - b² -bс
a²- аb- ас= ba-b²-bc
a(a – b - c)= b (a – b - c)
Отсюда a = b. То есть два произвольных числа равны.
Правила проведения внеклассного мероприятия:
Для того чтобы у учителя была возможность следить за правильностью выполнения заданий, команды фиксируют своё решение на бумаге.
Задание 1.
Право отвечать предоставляется той команде, которая справилась с заданием быстрее.
При этом учитель проверяет решение и у второй команды. Обе команды получают соответствующие баллы за правильные ответы.
В случае, если обе команды верно решили все четыре задачи, команде, справившейся с заданием первой, добавляется 1 балл за скорость.
Перед выполнением следующих заданий, по средствам жребия решают, какой команде выпадает право отвечать во втором задании. Далее во всех заданиях, кроме шестого, команды отвечают по очереди.
При этом, как и в первом задании, баллы за правильные решения получают обе команды.
Если команда, которая должна представить своё решение данного задания, затрудняется с ответом, право отвечать переходит к команде соперника.
Далее ответы команд снова чередуются.
Задание 2.
На выполнение этого задания даётся 3-5 минут.
Задание 3.
На выполнение этого задания даётся 3-5 минут.
Задание 4.
На выполнение этого задания даётся 3 минуты.
Задание 5.
На выполнение этого задания даётся 2 минуты.
Плюс команде, справившейся с заданием первой, добавляется балл за скорость.
Задание 6.
Задание на скорость.
Право отвечать и право заработать соответствующие баллы получает команда, которая первой догадалась до верного решения.
(Правила выполнения этого задания связаны с тем, что в данном случае трудно отследить решение задачи.)
При этом, если по прошествии 7 минут ни одна из команд не готова отвечать, решение задачи демонстрирует учитель.
Задание 7.
На выполнение этого задания даётся 1 минута.
Задание 8.
На выполнение этого задания даётся 7-10 минут.
Задание 9.
На выполнение этого задания даётся 7-10 минут.
Итоговая таблица баллов.
| № задания. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Количество баллов. | 4 +1 балл за скорость. | 1 | 2 | 1 | 1 +1 балл за скорость. | 2 | 2 | 3 | 3 |