Добавлен: 26.10.2023
Просмотров: 128
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Приложение 5
Урок математики в 9 классе с применением приемов критического мышления.
Тема: Вписанные в окружность и описанные около нее многоугольники.
Цель - закрепление новых знаний по теме.
Задачи:
-
Закрепить знания о вписанных в окружность и описанных около нее многоугольников.
-
Развитие критического мышления
-
Воспитание чувства коллективизма, сопереживания, стремления к совместному успеху.
Оборудование: учебник, компьютер, постеры, физминутки, раздаточный материал
Тип урока: урок закрепления новых знаний.
Приложение 5
Урок математики в 9 классе с применением приемов критического мышления.
Тема: Вписанные в окружность и описанные около нее многоугольники.
Цель - закрепление новых знаний по теме.
Задачи:
-
Закрепить знания о вписанных в окружность и описанных около нее многоугольников.
-
Развитие критического мышления
-
Воспитание чувства коллективизма, сопереживания, стремления к совместному успеху.
Оборудование: учебник, компьютер, постеры, физминутки, раздаточный материал
Тип урока: урок закрепления новых знаний.
Приложение 5
Урок математики в 9 классе с применением приемов критического мышления.
Тема: Вписанные в окружность и описанные около нее многоугольники.
Цель - закрепление новых знаний по теме.
Задачи:
-
Закрепить знания о вписанных в окружность и описанных около нее многоугольников.
-
Развитие критического мышления
-
Воспитание чувства коллективизма, сопереживания, стремления к совместному успеху.
Оборудование: учебник, компьютер, постеры, физминутки, раздаточный материал
Тип урока: урок закрепления новых знаний.
Закрепить знания о вписанных в окружность и описанных около нее многоугольников.
Развитие критического мышления
Воспитание чувства коллективизма, сопереживания, стремления к совместному успеху.
| Этап урока | Содержание | Примечание |
| 1.Орг. момент Проверка готовности к уроку. Психологический настрой на урок. 2. Вступительное слово учителя. Подведение к теме урока . 3. Фронтальный опрос по теме урока. 4. Выполнение заданий повторительно- обобщающего характера А- Инструктирование к выполнению заданий В- Проверка выполнения С- « Внедрение нового метода» 5. Оценивание. 6. Подведение итогов . 7. Дом.задание | Учитель проводит с уч-ся тренинг « Пожелание».
- Ребята! На сегодняшнем уроке мы закрепим материал, изученный на предыдущем уроке. Итак, внимание на доску О чем же пойдет речь на уроке (многоугольниках…окружности) - какой многоугольник называется правильным? -выведите ф-лу для вычисления угла правильного п-угольника? - чему равна сумма внешних углов правильного многоугольника, взятых по одному при каждой вершине? - выведите формулу для вычисления внешнего угла правильного п-угольника? ФИЗМИНУТКА Деление на группы по выбору учителя ( ученики разного уровня - « сильный», « средний», « слабый». ) Задание – индивид-ые карточки с заданием и инструкцией к выполнению. Взаимопроверка в группах. На данном этапе ученикам предлагается проверить знания ключевых понятий темы (Применение приема «ДА-НЕТ») Лист самооценивания Рефлексия. Ученикам предлагается Рефлексия учебной деятельности- Подведение итогов урока –« Составление мудрого дерева» ( учащиеся пишут на стикерах свои впечатления, результаты урока , что узнали нового, что повторили и обобщили). При письменных ответах пользуемся рефлексивным экраном ( на доске). сегодня я узнал… было интересно… было трудно… я выполнял задания… я понял, что… я научился… у меня получилось … я смог… в заключ. выставляя оценку своей работе на уроке - Какую работу выполняли на уроке ? | Тренинг направлен на улучшение психологического комфорта в классе, дружеское общение недружелюбно настроенных др. к др. одноклассников На доске-незаконченный кластер « Окружность» В центре -* ?*. На постерах определения, без указания термина. При опросе используется метод « Тонкие и толстые вопросы» (критич. мышление) Программированный опрос Учитель проводит по мере выполнения задания наблюдение - как работают в группе и выполняют задание ученики разного уровня. Наблюдение за взаимопроверкой , как реагируют ученики на замечания друг друга, объективно ли их оценивание. Данная работа носит творческий характер , предполагает включенность всех учеников в работу. Учитель ведет наблюдение за процессом взаимодействия в группе. Данный вид оценивания воспитывает в учениках объективное отношение к своей деятельности. Значение стадии рефлексии: 1) Происходит выведение знания на уровень понимания и применения. 2) Идет рефлексия своего процесса учения. 3) Для развития коммуникативных навыков крайне важен непосредственный живой обмен идеями. 4) Выражение новой информации своими словами позволяет лучше понять и принять ее. |
Приложение 6
Приём «З-У-Х».
Работа с таблицей ведется на всех трех стадиях урока. В начале урока, заполняя первую часть таблицы «Знаю», учащиеся составляют список того, что они знают или думают о данной теме. Через эту первичную деятельность ученик определяет уровень собственных знаний, к которым постепенно добавляются новые знания. Вторая часть таблицы - «Хочу узнать» - это определение того, что дети хотят узнать, пробуждение интереса к новой информации. После усвоения темы на стадии рефлексии учащиеся заполняют третью графу таблицы - «Узнали».
Пример. Алгебра 8 класс. Тема урока «График уравнения у = кх +b»
| «Знаю» | «Хочу узнать» | «Узнал» |
| Линейное уравнение вида ах + bу + с = 0 можно представить в виде у = кх +b, если b≠0 | Как зависит расположение графика у = кх + b от b Как по графику можно определить знак к и величину b Как по уравнению прямой можно определить положение графика на координатной плоскости | Коэффициент к отвечает за «крутизну» графика функции у = кх + b. Чем больше к, тем круче график |
| Графиком уравнения у = кх b,является прямая | Точка пересечения графика с осью Оу (0; b) позволяет найти b. Если b˃0, то график сдвигается вверх вдоль оси Оу, если b˂0 , то график сдвигается вниз вдоль оси Оу. | |
| Расположение графика у = кх +b зависит от знака к. Если b=0, а к˃0, то график лежит в I и III координатных четвертях. Если b=0, а к˂0, то график лежит во II и IV координатных четвертях. | ||
| По уравнениям графиков можно сделать выводы об их взаимном расположении. Если к равны, то прямые параллельны, если к не равны, то прямые пересекаются. |
Приложение 7
Прием «Верные и неверные утверждения».
На доске или слайде записаны верные и неверные утверждения. До изучения новой темы ученики должны прочитать и поставить «+» там, где они считают, что высказывание верное, а знак «-» там, где неверное. Ученики работают в парах. Затем предлагаю учащимся поделиться своим мнением с классом. Заслушав ответы учащихся, заполняю первый столбец таблицы (столбец А). Подводя итоги работы над таблицей, подвожу учеников к мысли, что отвечая на вопросы, мы пока не знаем, правы мы или нет. Ответы на вопросы можно найти, изучив материал параграфа, прочитав предложенный текст и др.
Ученики приступают к работе над текстом, а затем, по окончании работы, возвращаются к вопросам, рассмотренным в начале урока, делятся своим мнением с классом. В результате заполняется столбец Б. Но это пока еще не значит, что учащиеся правильно ответили на все вопросы. Окончательно таблица заполняется (столбец В) на стадии рефлексии, после обсуждения полученных результатов.
Пример 1. Геометрия 8 класс. Тема «Подобные треугольники»
| № п/п | Утверждения | А | Б | В |
| Верно (+), неверно (-) | ||||
| 1. | В геометрии фигуры одинаковой формы называют подобными | | | |
| 2. | Подобными являются любые два квадрата | | | |
| 3. | Подобными являются любые два треугольника | | | |
| 4. | Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника соответственно пропорциональны сходственным сторонам другого треугольника | | | |
| 5. |  ∆АВС∆МРК ВС и МК сходственные стороны 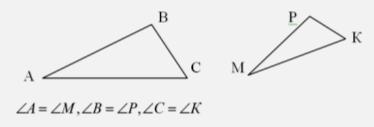 | | | |
| 6. | Отношение площадей подобных треугольников равно коэффициенту подобия | | | |
| 7. | Если 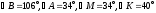 , то ∆АВС∆МРК , то ∆АВС∆МРК | | | |
| 8. | В ∆АВС и ∆А1В1С1 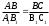 . Значит ∆АВС ∆А1В1С1 . Значит ∆АВС ∆А1В1С1 | | | |
| 9. | 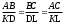 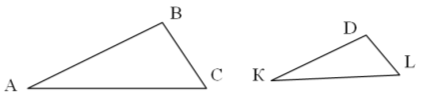 Значит ∆АВС ∆КDL | | | |
| 10. | В ∆АВС и ∆КDL АВ= 10, ВС=6, АС=14, KD=5, DL=3, KL=7 Значит ∆АВС ∆КDL | | | |
Пример 2. Алгебра 9 класс. Тема «Свойства линейных неравенств»
| № п/п | Утверждения | А | Б | В |
| Верите ли вы, что… (Верю (+), не верю (-)) | ||||
| 1. | Любое слагаемое можно перенести из одной части неравенства в другую, при этом знак неравенства не меняется | | | |
| 2. | Знаки ˂ и ˃ называются знаками нестрогого неравенства, а знаки ≥ и ≤ знаками строгого неравенства | | | |
| 3. | Знак «не меньше» - это ≤ | | | |
| 4. | К обеим частям неравенства можно прибавить одно и то же число, при этом знак неравенства не меняется | | | |
| 5. | Если из обеих частей неравенства вычесть одно и то же число, то знак неравенства изменится на противоположный. | | | |
| 6. | Обе части неравенства можно умножить на одно и то же положительное число, оставив знак неравенства без изменения. | | | |
| 7. | Обе части неравенства можно умножить на одно и то же отрицательное число, оставив знак неравенства без изменения. | | | |
| 8. | Любые неравенства можно складывать почленно | | | |
| 9. | Неравенства одного знака с положительными членами можно почленно перемножать | | | |
| 10. | Если а ˂ b и b ˂ с, то а ˂ с | | | |
Приложение 8
Прием «Кластер».
Это педагогическая стратегия, которая помогает учащимся свободно и открыто думать по поводу какой-либо темы. Разбивка на кластеры используется как на этапе вызова, так и на этапе рефлексии в основном для стимулирования мыслительной деятельности до того, как определённая тема будет изучена более тщательно. Часто применяю этот прием в качестве средства для подведения итогов того, что учащиеся изучили.
Иногда ключевое слово располагают вверху, ветви («гроздья») опускаются вниз, как гроздья винограда. Такой вариант хорошо воспринимается обучающимися и представляется более логичным.
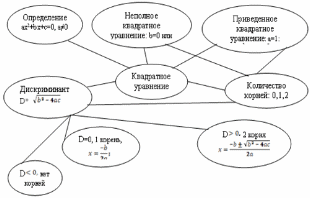
Пример: Кластер по теме «Квадратные уравнения» (Алгебра. 8 класс)
Приложение 9
Пример таблицы INCERT по теме «Многоугольники» (8 класс),
| V Уже знал | + Узнал новое | - Думал иначе | ? Есть вопросы |
|
|
|
|
Примеры синквейнов по различным темам:
| 1.Уравнение |
| 2.Линейное, квадратное (подобные, слагаемые…) |
| 3.Переносить члены, приводить подобные, делить на коэффициент при неизвестном, решать |
| 4.Равенство, содержащее неизвестное, обозначенное буквой |
| 5.Равенство |
| 1.Функция |
| 2.Возрастающая, четная (переменная, убывающая, нечетная, периодическая, монотонная, ограниченная, неограниченная, обратимая, линейная, квадратичная….) |
| 3.Строить, исследовать, задавать |
| 4.Каждому значению переменной х соответствует значение у |
| 5.Соответствие |
| 1.Параллелограмм |
| 2.Выпуклый, центрально симметричный |
| 3. Находить (периметр, площадь), строить, изучать, решать (задачи) |
| 4.Противоположные стороны попарно параллельны |
| 5. Четырехугольник |
| 1.Квадрат |
| 2. Симметричный, равносторонний, прямоугольный, правильный |
| 3.Находить (периметр, площадь), строить, изучать |
| 4.Прямоугольник, у которого все стороны равны |
| 5. Правильный многоугольник |
| 1.Квадрат |
| 2. Четырехугольный, равноугольный, равнодиагональный |
| 3. Измерять, чертить, исследовать |
| 4. Квадрат – необычная фигура |
| 5. Параллелограмм (ромб, прямоугольник) |
| 1.Параллелограмм |
| 2. Выпуклый |
| 3.Измеряем, изучаем, |
| 4.Четырехугольник, у которого противоположные стороны равны (диагонали в точке пересечения делятся пополам) |
| 5. Четырехугольник |
| 1.Неравенство |
| 2.Числовое, алгебраическое (верное, неверное, линейное, квадратное…) |
| 3.Сравнивать, преобразовывать, решать |
| 4.Два выражения, связанные знаками больше или меньше |
| 5. Сравнение |