Вычисляется базисное сопротивление:

_б = ^Н. (2.8)




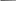
Н

Находятся параметры схемы замещения двигателя в физических величи-нах: активное сопротивление обмотки статора:

= ∙ б,Ом.

(2.9)

Индуктивное сопротивление рассеяния обмотки статора:
10


= ∙ _б, Ом. (2.10)
Активное сопротивление обмотки ротора, приведенное к обмотке статора:

= ∙ б,Ом.

(2.11)

Индуктивное сопротивление рассеяния обмотки ротора, приведенное к обмотке статора:

= ∙ _б, Ом. (2.12)
Индуктивное сопротивление контура намагничивания:

= ∙ б,Ом.

(2.13)

Найденные параметры схемы замещения позволяют рассчитать статиче-ские характеристики асинхронного двигателя, например, по формуле Клосса, т. е. без учета насыщения зубцов от полей рассеяния и вытеснения тока в стержнях беличьей клетки.

2.3. Определение параметров схемы замещения асинхронного двигателя по каталожным данным
Как правило, в каталогах [4] на асинхронные двигатели приводятся сле-дующие технические данные:

_Н − номинальная мощность двигателя, кВт;

_Н − номинальное фазное напряжение, В;

_Н − номинальный ток статора двигателя, А;
_Н − номинальная частота вращения, об⁄мин; _Н − номинальное скольжение, о. е.;
_Н − коэффициент полезного действия электродвигателя в режиме номи-нальной мощности (100%-я нагрузка), %;

cos _Н − коэффициент мощности в режиме номинальной мощности, о. е.;

• 
  П – кратность пускового тока, о. е.;
  

Н

П = ^МП – кратность пускового момента, о. е.;




М_Н

= ^Мкр – кратность максимального момента, о. е.;

---

М_Н

• 
  – кратность минимального момента, о. е.
  

Н
Эти данные позволяют определить параметры схемы замещения при сле-дующих основных допущениях:

1) магнитные и механические потери в двигателе составляют 0,02 ∙ _Н;

2. 
   активные сопротивления статорной и роторной обмоток полагаются не-
   

зависящими от режима работы двигателя, т. е. эффекты вытеснения то-ка не учитываются.
Определяется ток холостого хода асинхронного двигателя:

=

∗

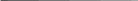
Н(1 −

Н)/(1 −

∗

Н)

,

(2.14)

1 −

∗(1 −

Н)/(1 −

∗

Н)

где Н – номинальный ток статора двигателя, А;

Н = ( − Н)/ – номинальное скольжение, о. е.;

– синхронная частота вращения, об/мин;

Н – номинальное фазное напряжение, В;

=

∗

∙ Н

(2.15)

∙ Н ∙

∗

∗

---

– ток статора двигателя при частичной загрузке, А;

• 
  – коэффициент мощности при частичной загрузке, о. е.; − КПД электродвигателя при частичной загрузке, о. е.;
  

∗

• 
  = ⁄ _Н – коэффициент загрузки двигателя, о. е.;
  

– мощность двигателя при частичной загрузке, кВт.
Коэффициенты мощности и КПД при частичной загрузке в технической литературе приводятся редко, а для целого ряда серий электрических машин такие данные в справочной литературе отсутствуют. Эти параметры можно оп-ределить, руководствуясь следующими соображениями:

• 
  современные асинхронные двигатели проектируются таким образом, что наибольший КПД достигается при загрузке на 10÷15 % меньше номинальной
  

3. 
   Двигатели рассчитываются так потому, что большинство из них, в силу стандартной дискретной шкалы мощностей, работают с некоторой недогрузкой.
   

Поэтому КПД при номинальной нагрузке и нагрузке _∗ = 0,75 практически равны между собой, т. е.

_Н≈ _, ;

• 
  коэффициент мощности при той же нагрузке ( _∗ = 0,75) сильно от-личается от коэффициента мощности при номинальной нагрузке, причем это
  

отличие в значительной степени зависит от мощности двигателя.
Из формулы Клосса определим выражение для расчета критического скольжения:

+ ()−1−2∙Н∙ ∙(

− 1)

К =

Н

, (2.16)

1−2∙

Н ∙

∙ (

− 1)

=

,

(2.17)

(

∙

)

---

С	= 1 +			/(2 ∙	∙	Н) .			(2.18)
Значение коэффициента , согласно источнику [4], находится в диапазоне
0,6÷2,5. Определим коэффициент [8]:
А =	∙ Н		∙	1 −		Н		,	(2.19)
				2 ∙	∙	∙
							Н

тогда активное сопротивление ротора, приведенное к обмотке статора асин-хронного двигателя:

=	+ 1
					, Ом.		(2.20)
Активное сопротивление статорной обмотки можно найти по следующему
выражению:
=		∙		∙	, Ом.		(2.21)
Определим параметр , который позволяет найти индуктивное сопротив-
ление короткого замыкания кн:
=	1			−	.		(2.22)
			К

---

Очевидно, что при отрицательном подкоренном выражении, первоначаль-но принятое значение необходимо изменить. Тогда индуктивное сопротивле-ние короткого замыкания:

кн= ∙С∙ .

(2.23)

Для того чтобы выделить из индуктивного сопротивления короткого за-мыкания _кн сопротивления рассеяния фаз статора _Н и ротора _Н, вос-пользуемся соотношениями [8], которые справедливы для серийных асинхрон-ных двигателей. Индуктивное сопротивление рассеяния фазы роторной обмот-ки, приведенное к статорной, может быть рассчитано по уравнению:

Н =0,58∙	кн	, Ом.	(2.24)

Индуктивное сопротивление рассеяния фазы статорной обмотки может быть определено по следующему выражению:

Н = 0,42 ∙ кн, Ом.

(2.25)

ЭДС ветви намагничивания , наведенная потоком воздушного зазора в обмотке статора в номинальном режиме, равна:




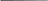
Е _Н= ( _Н∙ _Н− ∙ _Н) + _Н∙ 1− _Н− _Н∙ _Н ,(2.26)
тогда индуктивное сопротивление контура намагничивания:
13


_Н = ^Н . (2.27)



Приведенная методика дает удовлетворительное схождение расчетных ме-ханических характеристик и механических характеристик, построенных по трем паспортным точкам на рабочем участке механической характеристики, т. е. при изменении скольжения от 0 до _К. Используя параметры схемы за-мещения, можно произвести расчет механических и электромеханических ха-рактеристик асинхронного двигателя.

3. 1   2   3   4   5   6   7   8   9   ...   16

---

Смотрите также файлы

• Курсовая работа Дисциплина Уголовноисполнительное право Тема Правовое положение осужденных к лишению свободы. курсант 315 учебной группы.docx

• Учр.docx

• Тема Знакомство с базой практики 2.docx

• Практическое задание 1,2,3.doc

• Расходы (детально) На 01. 01. 2021.doc