РАСЧЕТ ЕСТЕСТВЕННЫХ МЕХАНИЧЕСКИХ

• 
  ЭЛЕКТРОМЕХАНИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕКТРОДВИГАТЕЛЕЙ
  

3.1. Двигатель постоянного тока независимого возбуждения
Естественной электромеханической (механической) характеристикой дви-гателя постоянного тока называют зависимость угловой скорости двигателя от его тока якоря (момента ), полученную при номинальной схеме включе-ния двигателя, номинальных параметрах напряжения обмоток якоря и возбуж-дения и отсутствии добавочных сопротивлений в цепях двигателя.
Естественная электромеханическая характеристика рассчитывается по уравнению:

=

Н

− ∙

ДВ гор

.

(3.1)

с

с

Естественная механическая характеристика двигателя постоянного тока

строится по выражению:

=

Н

− М ∙

ДВ гор

.

(3.2)

с

с

---

3.2. Асинхронный двигатель
Для расчета электромеханических и механических характеристик асин-хронного двигателя необходимо воспользоваться его математической моделью, которая в общем случае представляется различными схемами замещения. Наи-более простой и удобной для инженерных расчетов асинхронного двигателя является Т-образная схема замещения.

Основные уравнения асинхронного двигателя, соответствующие принятой схеме замещения:

14

ф−Е−∙	∙ ̅− ∙ ̅=0;
+∙̅∙	̅+		∙ ̅=0;	(3.3)
̅+	̅−	̅= 0,

где _ф – фазное напряжение обмотки статора двигателя, В;

• 
  – ЭДС обмотки статора, В;
  

– индуктивное сопротивление рассеяния обмотки статора, Ом;
– активное сопротивление обмотки статора, Ом;

• 
  индуктивное сопротивление рассеяния обмотки ротора, приведенное
  
• 
  обмотке статора, Ом;
  

• 
  активное сопротивление обмотки ротора, приведенное к обмотке статора, Ом;
  

– ток обмотки статора, А;

• 
  ток обмотки ротора, приведенной к обмотке статора, А;
  

– ток холостого хода обмотки статора, А.
Ток ротора , приведенный к обмотке статора асинхронного двигателя, определяется зависимостью, получаемой непосредственно из схемы замещения асинхронного двигателя:

=

ф

,

(3.4)

±

+

+ кн

где кн =

+

– индуктивное сопротивление короткого замыкания.

Уравнение

= ( ) называется

электромеханической

характеристикой

---

асинхронного двигателя.
Для асинхронного двигателя с короткозамкнутым ротором представляет интерес другая электромеханическая характеристика: = ( ), отражающая зависимость тока статора от скольжения . Ток статора определяется путем сложения вектора намагничивания ^̅и вектора тока ротора ^̅:

̅= ̅+ ̅.

(3.5)

Полагая ток намагничивания асинхронного двигателя реактивным, ток

статора через приведенный ток ротора можно найти по формуле:

=

+ +2∙

∙

∙

,

(3.6)

где

=

кн

.

(3.7)

+

+

кн

---

Основной выходной координатой силового привода является электромаг-нитный момент, значение которого для асинхронного двигателя определяется по выражению:

М =	∙	ф ∙
			,	(3.8)
	∙∙(+∙	)+(+)

где – число фаз статора.
Механическая характеристика асинхронного двигателя имеет критический

момент и критическое скольжение, которые находятся при условии

= 0.

Тогда критический момент будет равен:

К =

∙

ф

.

(3.9)

± (

2 ∙

∙

+ кн)

Критическое скольжение будет равно:

К = ±

.

(3.10)

+

кн

---

Знак «+» означает, что критический момент и скольжение относятся к дви-гательному режиму, знак «–» – к генераторному режиму рекуперативного тор-можения.
Уравнение механической характеристики асинхронного двигателя (3.8) можно преобразовать к более удобному для использования выражению – фор-муле Клосса:

	2 ∙		К(1 +		∙	К)
=							,	(3.11)
	К	+		+ 2 ∙	∙
						К
			К

где = – коэффициент.
Двигатели средней и большой мощности имеют малое активное сопротив-ление , в этом случае коэффициентом можно пренебречь, а предыдущее выражение (3.11) преобразуется в упрощенную формулу Клосса:

=	2 ∙	К	.	(3.12)

• 
  +
  

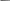
К
Задаваясь скольжением, можно построить механические характеристики асинхронного двигателя.

4. 1   2   3   4   5   6   7   8   9   ...   16

---

Смотрите также файлы

• Курсовая работа Дисциплина Уголовноисполнительное право Тема Правовое положение осужденных к лишению свободы. курсант 315 учебной группы.docx

• Учр.docx

• Тема Знакомство с базой практики 2.docx

• Практическое задание 1,2,3.doc

• Расходы (детально) На 01. 01. 2021.doc