Точечной оценкой θ* параметра θ называется числовое значение этого параметра, полученное по выборке объема n

• 
  Интервальные
  

Интервальной оценкой параметра тета называется числовой интервал (θ1; θ2), который с определенной вероятностью накрывает (содержит) неизвестное значение параметра.

10. 
    Свойства статистических оценок: несмещенность, состоятельность, эффективность.
    

• 
  Несмещенность (оценка совпадает с параметром θ). Стат оценка параметра θ называется несмещенной, если ее мат ожидание (среднее значение) равно оцениваемому параметру при любом объеме выборки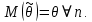 В противном случае мат ожидание не равно параметру θ оценка называется смещенной. В этом случае разность между мат ожиданием и параметром называют смещением или систематической ошибкой оценивания.
  

Св-во несмещенности является желательным, но не обязательным.

• 
  Эффективность – оценка обладает наименьшей степенью случайных отклонений от параметра θ.
  

Несмещенная оценка параметра θ называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра, т.е. если ее дисперсия минимальна при заданном объеме выборки. Эффективность определяется отношением:



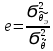
Где в числителе дисперсия эффективной оценки, а в знаменателе – дисперсия данной оценки.

Чем ближе е к 1, тем эффективней оценка.

Требование эффективности является желательным, но не обязательным.

• 
  Состоятельность – оценка стремится к параметру θ с ростом объема выборки (n).
  

Оценка параметра называется состоятельной, если она удовлетворяет ЗБЧ (т.е. при n→∞ сходится по вероятности к оцениваниваемому параметру)

Другими словами, для любого положительного числа ε выполняется условие:



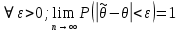
Свойства состоятельности является обязательным для любого правила оценивания.

11. 
    Точечная оценка математического ожидания.
    

Пусть изучается СВ Х с мат ожиданием а.

Несмещенной точечной оценкой мат ожидания М(Х) = 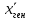является выборочная средняя.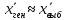

12. 
    Точечные оценки дисперсии и среднего квадратического отклонения.
    

---

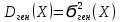– генеральная дисперсия имеет 2 точечные оценки:

• 
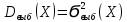  - выборочная дисперсия, которая является смещенной оценкой
  
• 
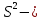  исправленная выборочная дисперсия (несмещенная)
  

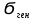имеет 2 точечные оценки:

• 
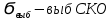  (стандартное отклонение) – смещенная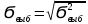
  
• 
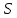  - исправленное выборочное СКО 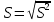(несмещенная)
  

13. 
    Точечная оценка генеральной доли.
    

Пусть генеральная совокупность содержит N элементов, из которых М обладают некоторым признаком А. Тогда доля единиц, обладающих признаком А в генеральной доли обозначается

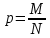, где N- объем генеральной совокупности, M – число элементов в генеральной совокупности с признаком А.

Пусть n – объем выборки; m – число элементов с признаком А в выборке. Тогда величина 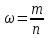называется выборочной долей.

Генеральную долю можно рассматривать как вероятность появления события А в биномиальном законе распределения СВ Х, а выборочную долю – как относительную частоту этого события в n независимых испытаниях.

Несмещенной и состоятельной точечной оценкой генеральной доли является выборочная доля ω, т.е.

14. 
    Методы нахождения точечных оценок: метод моментов, метод максимального правдоподобия.
    

Наиболее распространенные методы:

• 
  Метод моментов (ММ)
  
• 
  Метод максимального правдоподобия (ММП)
  
• 
  Метод наименьших квадратов (МНК)
  

Метод моментов – это приравнивание теоретических моментов распределения (т.е. начальных αk или центральных μk) СВ Х к соответствующим эмпирическим (выборочным) моментам, найденным по выборке, с последующим решением полученного уравнения (системы уравнений).

I Если теоретическое распределение задается одним параметрам, то для нахождения точечной оценки неизвестного параметра необходимо решить одно уравнение вида:

---

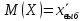
II Если теоретическое распределение задается двумя параметрами, то для их оценки необходимо решить систему из двух уравнений вида:



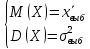
Достоинства и недостатки ММ:

• 
  Неприменим, когда моменты генеральной совокупности нужного порядка не существуют
  
• 
  Оценки, полученные данным методом, являются состоятельными, чего достаточно для решения многих задач
  
• 
  Однако по эффективности эти оценки не являются наилучшими, их эффективность часто значительно меньше единицы
  
• 
  ММ часто применяют на практике, т.к. он сводится к простым вычислениям.
  

Метод максимального правдоподобия (ММП).

В качестве оценки неизвестного параметра θ СВ Х выбирается то его значение, при котором полученное значение выборки имеет наибольшую вероятность или плотность вероятности (для дискретных и непрерывных СВ соответственно).

Использование метода сводится к нахождению максимума функции одной или нескольких переменных.

Оценкой наибольшего правдоподобия параметра θ является такое его значение θ*, при котором функция правдоподобия L имеет максимум.

Алгоритм применения ММП:

1. 
   По данной выборки {xn} построить функцию правдоподобия L(x1,x2…xn;θ)
   
2. 
   Найти натуральный логарифм функции правдоподобия (упростить)
   
3. 
   Найти первую производную LnL
   
4. 
   Решить уравнение правдоподобия (LnL)’=0
   
5. 
   Найти критические точки θ* -крит
   
6. 
   Убедиться, что найденная точка θ* является точкой максимума, воспользовавшись достаточным условием максимума:
   
   1. 
      Найти вторую производную (LnL)”
      
   2. 
      Если (LnL)” | θ*<0 , то θ* - точка максимума.
      

Таким образом найденная точка θ* будет являться оценкой максимального правдоподобия параметра θ.

Оценки, полученные ММП являются состоятельными и эффективными, но не всегда несмещенными.

Недостатки ММП:

• 
  Решение уравнения правдоподобия бывает трудным
  
• 
  Нужно знать закон распределения СВ Х, что на практике часто бывает невозможным
  

15. 
    Понятие доверительной вероятности и доверительного интервала. Точность оценки.
    

Задача интервального оценивания – по данным выборки построить числовой интервал (θ1; θ2), относительно которого с заранее выбранной вероятностью γ можно сказать, что внутри этого интервала находится оцениваемый параметр.

---

Интервальной оценкой параметра θ называется числовой интервал (θ1; θ2), который с заданной вероятностью гамма накрывает (содержит) неизвестное значение параметра 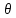т.е. для которого выполняется условие: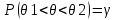

Величина 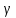– есть вероятность события, что параметр θ отличается от своей точечной оценки на величину, не превосходящую некоторого положительного числа δ

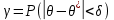, где δ- точность оценки

Интервал (θ1; θ2) называется доверительным интервалом или интервальной оценкой, а вероятность γ – доверительной вероятностью, уровнем доверия или надежностью оценки.

Число α=1-γ – уровень значимости:

• 
  Значение α(γ) выбирают заранее
  
• 
  Выбор зависит от конкретно решаемой задачи
  
• 
  Обычно выбирают: γ= 0,9; 0,95; 0,99; 0,999
  
• 
  Или α=0,1; 0,05; 0,01; 0,001
  
• 
  Ширина интервала h=θ2- θ1 существенно зависит от объема выборки n (уменьшается с ростом n) и от значения доверительной вероятности (увеличивается с приближением γ к единице)
  

16. 
    Основные законы распределения математической статистики.
    

Распределение Хи-квадрат (Пирсона) с k=n степенями свободы называют распределение суммы квадратов независимых СВ, распределенных по стандартному нормальному закону, т.е.

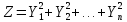, где Yi – независимы и имеют одно и то же нормальное стандартное распределение, т.е. Yi⁓N(0,1); M(Yi)=0, D(Yi)=1

Число слагаемых называется числом степеней свободы распределения ( это параметр формы кривой 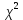-распределения)

Обозначается Z⁓

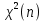
СВ, распределенная по закону 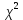принимает только неотрицательные значения, т.е. Z≥0

Кривая 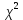-распределения одновершинная, асимметричная. С ростом n вершина кривой сдвигается вправо от начала координат и 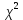- распределение медленно приближается к нормальному.

Числовые характеристики: M(

---

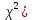
=n; D( =2n

Распределение используется при интервальном оценивании дисперсии, проверке статистических гипотез согласия, однородности, независимости, при проверке значимости коэффициента корреляции и в других задачах статистического анализа данных.

Распределение Стьюдента или t-распределение с k степенями свободы называется распределение СВ 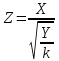, где X- СВ, распределенная по стандартному нормальному закону (X⁓N(0,1)), а Y имеет распределение Хи-квадрат с k степенями свободы, т.е. Y⁓ 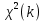. Обозначение Z⁓t(k). СВ, распределенная по закону Стьюдента принимает любые значения.

Распределение Стьюдента симметрично относительно 0: если X⁓t(k), то и (-X) ⁓t(k).

Числовые характеристики: M(t)=Mo(t)=Me(t)=0; D(t)= 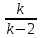, k>2

Кривая распределения Стьюдента по сравнению с кривой нормального распределения является более пологой. При k→∞, t-распределение быстро приближается к нормальному, при k>30 они уже практически неразличимы.

Распределение Стьюдента применяют при интервальном оценивании мат ожидания и других параметров, при проверке гипотез о значениях мат ожиданий, оценке значимости коэф-ов регрессии, гипотез об однородности выборок и тд.

Распределением Фишера с k1 и k2 степенями свободы называется распределение СВ 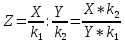, где X и Y – независимые СВ распределенные по закону Пирсона, т.е. Х⁓ 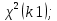Y⁓

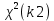
Обозначение Z⁓F(k1,k2). СВ, распределенная по закону Фишера может принимать только неотрицательные значения, т.е. Z≥0

Числовые характеристики:





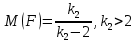
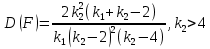
С ростом числа степеней свободы распределение Фишера приближается к нормальному. Применяется при проверке гипотез о равенстве дисперсий, о статистической значимости уравнения регрессии.

17. 
    Интервальная оценка генеральной средней (математического ожидания).
    

---

Смотрите также файлы

• Возможно ли привлечение Сапожникова к административной ответственности.doc

• Мдк. 01. 01 Право социального обеспечения.docx

• Музыка в сопи.docx

• 1 Конвективный способ.docx

• Лабораторная работа 11 (5) определение момента инерции колеса и момента силы трения.docx