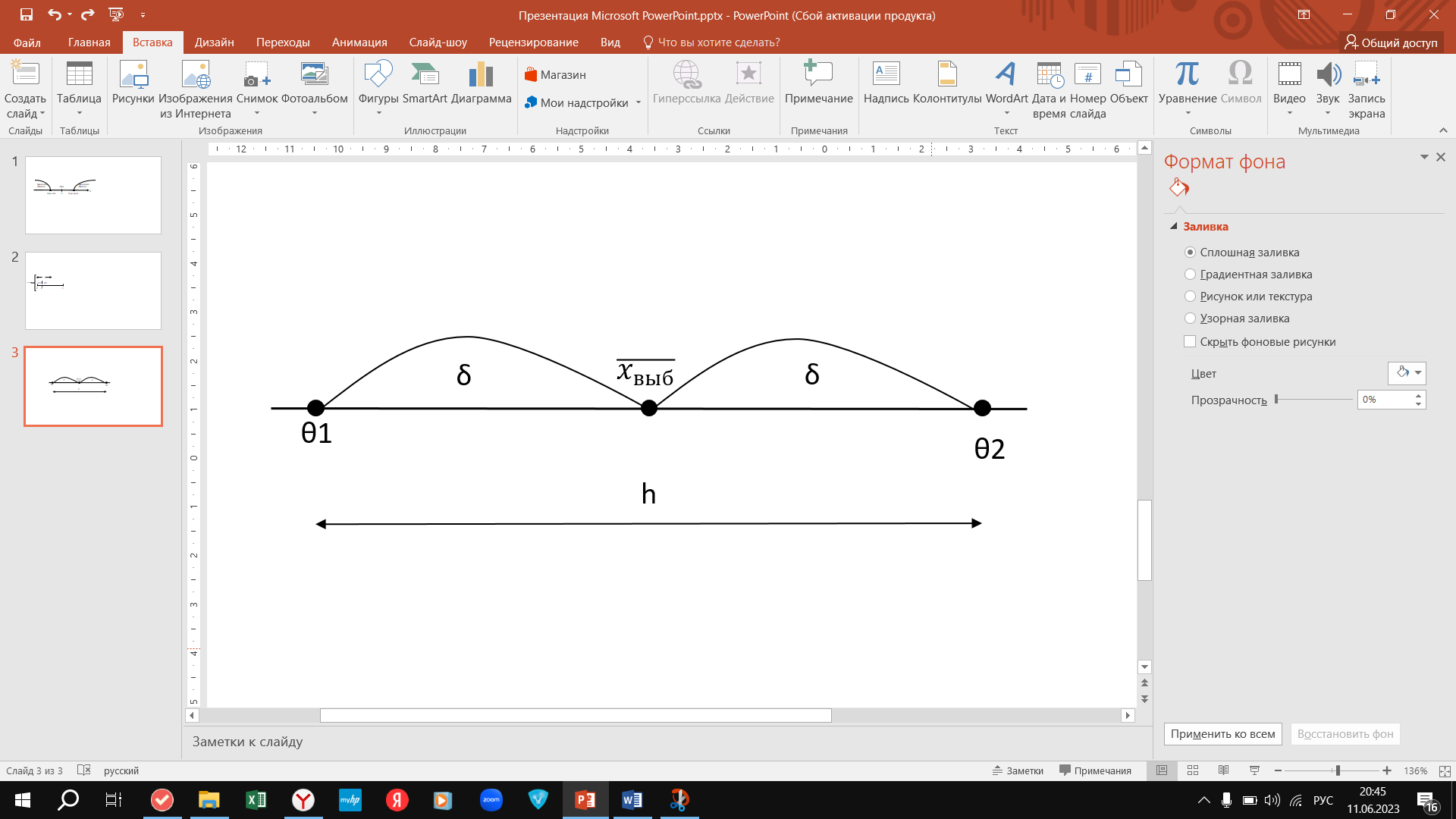
В качестве интервальной оценки мат ожидания выступает точечная оценка – выборочная средняя – относительно которой строится симметричный интервал.



Правила построения доверительного интервала зависят от того, известна или неизвестна генеральная дисперсия

• 
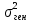
  Доверительный интервал с заданной надежностью γ неизвестного математического ожидания с известной генеральной дисперсией имеет вид:
  

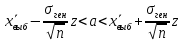
Где Z – квантиль стандартного нормального распределения уровня 1-α/2

В Excel: =НОРМ.СТ.ОБР((1+γ)/2)

Число δ= 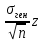– точность оценки мат ожидания. Тогда доверительный интервал для генеральной средней можно записать в виде: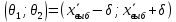

Ширина интервала h= 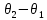= 2δ

• 
  Доверительный интервал с заданной надежностью γ неизвестного математического ожидания с неизвестной генеральной дисперсией имеет вид:
  

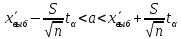, где 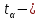квантиль распределения Стьюдента (для двусторонней области) соответствующий k=n-1 степеням свободы и уровню значимости α

В Excel: = СТЬЮДЕНТ.ОБР.2Х(α;k=n-1)

Число δ= 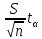– точность оценки мат ожидания.

18. 
    Интервальная оценка генеральной дисперсии и генерального СКО.
    

Основой интервальной оценки генеральной дисперсии является статистика 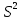(Исправленная выборочная дисперсия или исправленное выборочное СКО – S)

Интервал в отличии от генеральной средней для генеральной дисперсии строится несимметричный.

Доверительный интервал с заданной надежностью γ для генеральной дисперсии имеет вид:



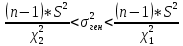
Где критические точки определяются по таблице распределения Пирсона:

---

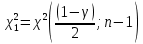
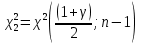
Замечание: значения критических точек распределения можно найти с помощью функций Excel:

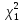=ХИ2.ОБР( )

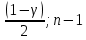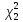=ХИ2.ОБР( )

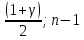Доверительный интервал для генерального СКО имеет вид:

19. 
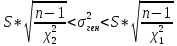
    Интервальная оценка генеральной доли.
    

Доверительный интервал для генеральной доли с заданной надежностью γ строится симметрично относительно выборочной доли и имеет вид:

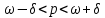
Где – выборочная доля

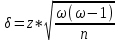точность оценки генеральной доли

Z - квантиль стандартного нормального распределения уровня

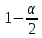
Z=НОРМ.СТ.ОБР((1+ γ)/2)

20. 
    Понятие статистической гипотезы. Параметрические и непараметрические гипотезы.
    

Статистическая гипотеза – это некоторое высказывание относительно генеральной совокупности, проверяемое по выборочным данным.

Статистическая гипотеза – это любое предположение о виде неизвестного распределения или о параметрах известного закона распределения.

Статистические гипотезы:

• 
  Параметрические
  
  • 
    Простые
    
  • 
    Сложные
    
• 
  Непараметрические
  

Параметрические гипотезы – это утверждения о значении параметров распределения известного вида:

• 
  Простые – утверждения о том, что значение неизвестного параметра генеральной совокупности равно одному заданному числу
  
• 
  Сложные – гипотезы, не являющиеся простыми
  

Непараметрические гипотезы – это утверждения о виде неизвестного распределения

21. 
    Нулевая и альтернативная гипотеза. Типы альтернативных гипотез.
    

Выдвинутая гипотеза называется нулевой (основной). Н0 – нулевая гипотеза. По отношению к основной гипотезе можно сформулировать альтернативную (конкурирующую) противоречащую ей, т.е. гипотезу противоположную Н0. Н1 – альтернативная гипотеза.

Н0 и Н1 – это два предположения, из которых в результате статистической проверки должно быть выбрано только одно.

---

Проверить статистическую гипотезу значит установить, согласуются ли данные, полученные из выборки с этой гипотезой.

Статистическими методами гипотезу можно только опровергнуть или не опровергнуть, но не доказать!!!
Примеры параметрических гипотез:

• 
  Н0: мат ожидание СВ Х равно 2 (нулевая, основная)
  
• 
  Н1: a≠2 – двусторонняя сложная гипотеза
  
• 
  Н1: а>2 – правосторонняя сложная гипотеза
  
• 
  Н1: а<2 – левосторонняя сложная гипотеза
  
• 
  Н1: а=1,9 – простая левосторонняя гипотеза
  
• 
  Н1: а=2,1 – простая правосторонняя гипотеза
  

22. 
    Задача проверки статистических гипотез. Понятие статистического критерия.
    

Сопоставление высказанной гипотезы о генеральной совокупности с имеющимися выборочными данными, сопровождаемое количественной оценкой степени достоверности получаемого вывода и осуществляемое с помощью того или иного статистического критерия называется проверкой статистических гипотез.

Статистический критерий К (или стат тест) – это правило (формула), по которому определяется мера расхождения результатов выборочного наблюдения с высказанной гипотезой Н0, т.е. согласно которому принимается решение, принимать или отклонять нулевую гипотезу.

Основу критерия представляет специально составленная выборочная характеристика (СВ или статистика) 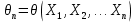- точечное или приближенное распределение которой неизвестно.

23. 
    Наблюдаемое и критическое значения статистического критерия.
    

Значение критерия, рассчитываемое по специальным правилам (по формулам) на основании выборочных данных называют наблюдаемым значением критерия (Kнабл)

Множество значений критерия К:

• 
  Область допустимых значений (область принятия нулевой гипотезы)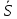 – совокупность всех значений критерия К, при которых нулевая гипотеза Н0 не отклоняется
  
• 
  Критическая область S – совокупность всех значений критерия К, при которых нулевая гипотеза отклоняется в пользу конкурирующей Н1.
  

Значения критерия, разделяющие области S и 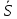, определяемые на заданном уровне значимости α по таблицам распределения (инструментальными средствами) СВ К, выбранной в качестве критерия, называют критическими точками (Ккрит)

---

24. 
    Критическая область и ее типы. Область принятия гипотезы.
    

Вид критической области зависит от того, какая гипотеза выдвинута в качестве альтернативной:

• 
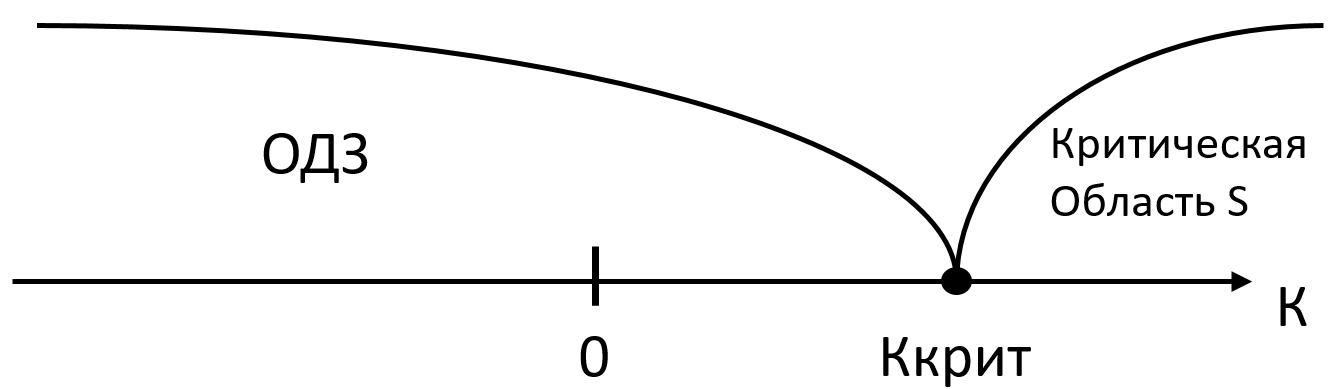
  Если конкурирующая гипотеза правосторонняя (Н1: a>2), то и критическая область S правосторонняя. В этом случае будет одна критическая точка, которая принимает положительные значения (Ккрит.прав.>0)
  

• 
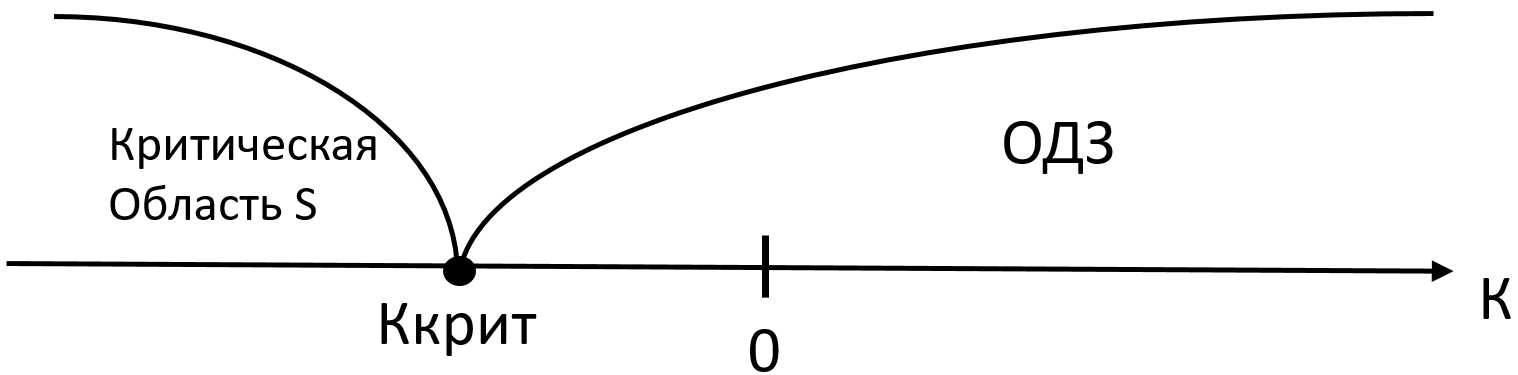
  Если конкурирующая гипотеза левосторонняя (Н1: а<2), то и критическая область S левосторонняя. В этом случае будет одна критическая точка, принимающая отрицательные значения. (Ккр.лев.<0)
  

• 
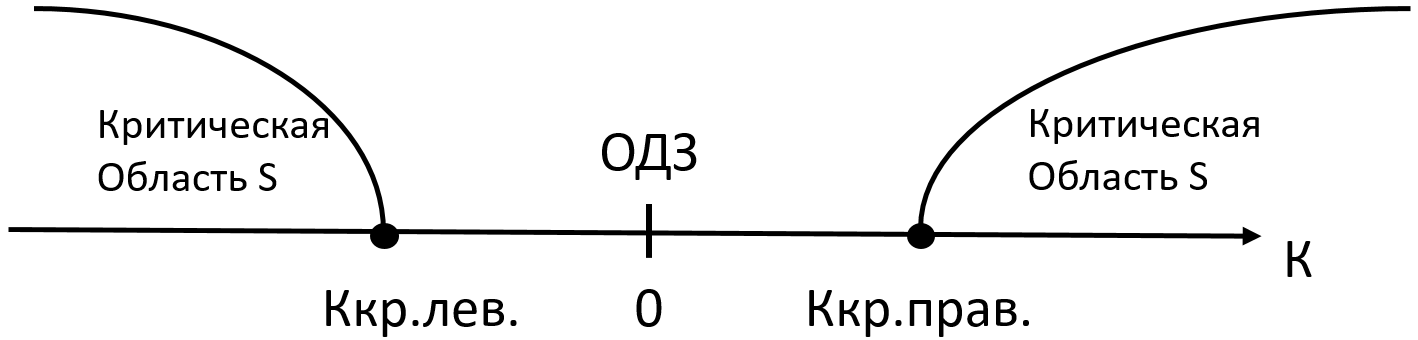
  Если конкурирующая область двусторонняя (Н1: a≠2), то и критическая область S будет двусторонняя. В этом случае будет 2 критических точки (Ккр.лев<0 и Ккр.прав>0), которые будут симметричны относительно нуля.
  

25. 
    Основной принцип проверки статистических гипотез.
    

Основной принцип проверки статистических гипотез:

• 
  Если наблюдаемое значение критерия (Кнабл) принадлежит критической области S, то нулевая гипотеза отклоняется в пользу конкурирующей гипотезы Н1
  
• 
  Если наблюдаемое значение критерия (Кнабл) принадлежит ОДЗ, то нулевую гипотезу Н0 нельзя отклонять.
  

26. 
    Общая схема проверки статистических гипотез.
    

1. 
   Располагая выборкой x1,x2…xn сформулировать основную (H0) и альтернативную (H1) гипотезы
   
2. 
   Выбрать уровень значимости α для проведения проверки
   
3. 
   По виду Н0 выбрать статистический критерий для ее проверки
   
4. 
   На основании данных выборки по специальному алгоритму (формуле) найти наблюдаемое значение критерия Кнабл
   
5. 
   По таблицам (формулам Excel) распределения СВ К, выбранной в качестве статистического критерия, найти критическое значение (критическую точку или точки)
   
6. 
   Исходя из типа конкурирующей гипотезы Н1 определить тип критической области S
   
7. 
   Посмотреть, какой области (S или ) принадлежит наблюдаемое значение критерия
   
8. 
   Сделать вывод о принятии или отклонении нулевой гипотезы.
   

Замечание: даже в том случае, если Н0 нельзя отклонить, это еще не значит, что данное предположение о генеральной совокупности является единственным верным, просто ему не противоречат имеющиеся выборочные данные. Таким свойством могут обладать и другие гипотезы.

---

27. 
    Ошибки первого и второго рода. Мощность критерия.
    

При проверке гипотезы могут быть приняты неправильные решения, т.е. могут быть допущены ошибки первого и второго рода.

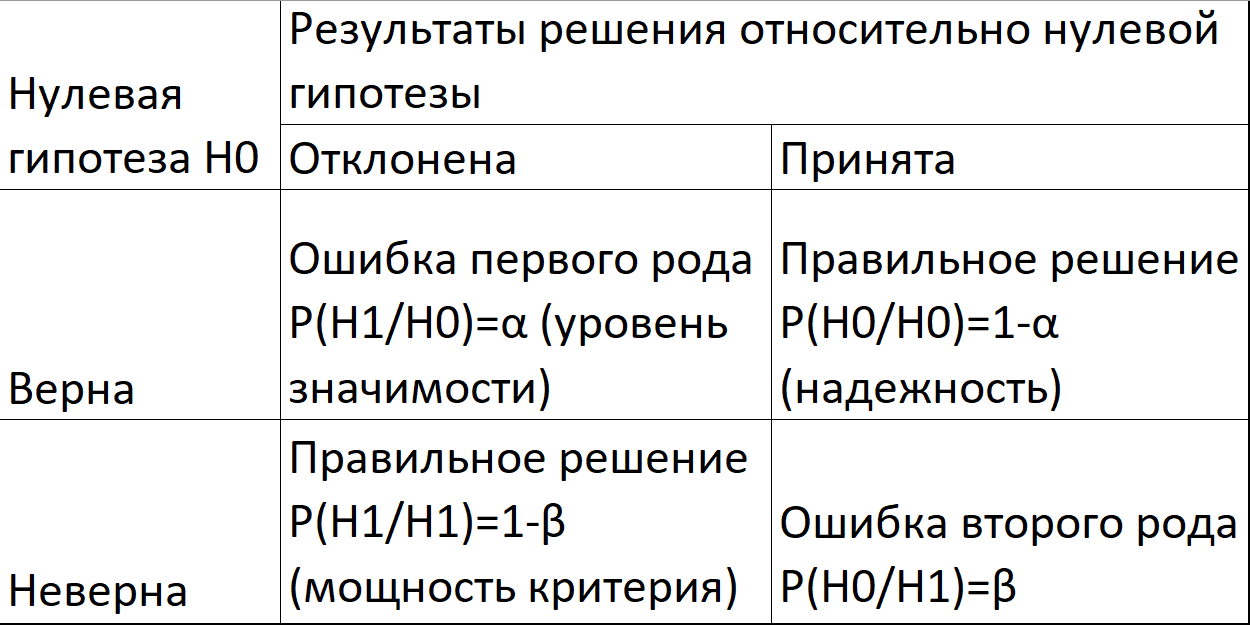
Ошибкой первого рода называется ошибка, возникающая, когда нулевая гипотеза отклоняется в то время как в действительности в генеральной совокупности она является справедливой. Вероятность совершить ошибку первого рода называется уровнем значимости (или размером критерия) и обозначается α.

Ошибкой второго рода называется ошибка, возникающая, когда Н0 принимается, в то время как на самом деле в генеральной совокупности она является ошибочной, а справедлива альтернативная Н1.

Вероятность допустить ошибку второго рода называется β

Вероятность 1- β, т.е. вероятность не допустить ошибку второго рода называют мощностью критерия (или функцией мощности)

Выбор статистического критерия и критической области осуществляют таким образом, чтобы мощность критерия была максимальной.

Критерий называют наиболее мощным, если из всех критериев с заданным уровнем значимости α, он имеет наибольшую мощность (наименьшее значение β)

Риски при проверке гипотез

28. 
    Наблюдаемый уровень значимости (р-значение/p-value)
    

Наблюдаемым уровнем значимости (или р-значением или p-value) гипотезы Н0, проверяемой по выборке x1,x2…xn с помощью критерия K(x1,x2…xn) называется наименьшее значение α, при котором нулевая гипотеза отклоняется



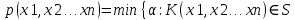
Ещё одна интерпретация p-значения – это вероятность, с которой (при условии истинности H0) могла бы реализоваться полученная выборка или любая другая выборка с еще менее вероятным наблюдаемым значением статистики К.

СВ р(х1,х2…xn) имеет равномерное распределение.

• 
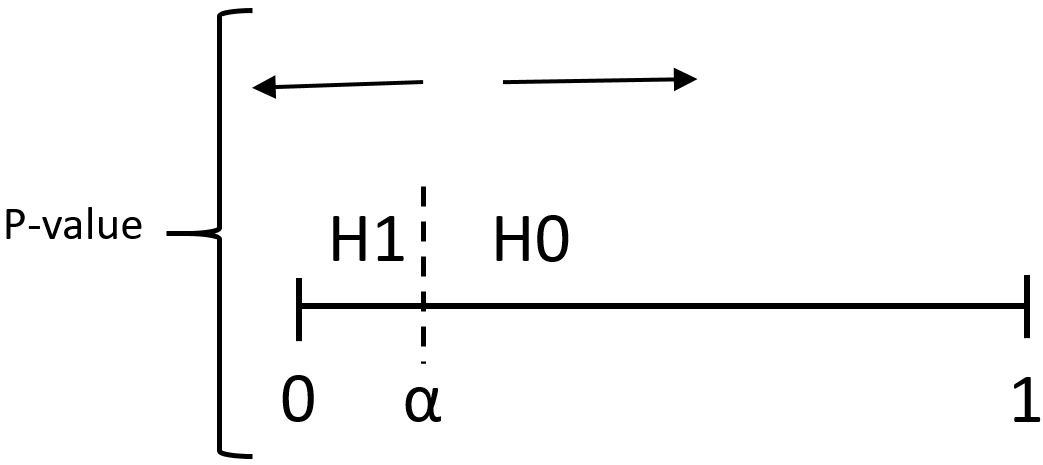
  Если р(х1,х2…xn)<α, то есть основания отклонять Н0
  
• 
  Если р(х1,х2…xn)≥α, то нет оснований отклонять Н0
  

Поэтому на практике, чем меньше р-значение, тем меньше вероятность ошибиться, отклонив нулевую гипотезу и тем выше уверенность в том, что необходимо отвергнуть Н0.

29. 
    Гипотезы о равенстве средних 2-х нормально распределенных генеральных совокупностей.
    

---

Смотрите также файлы

• Возможно ли привлечение Сапожникова к административной ответственности.doc

• Мдк. 01. 01 Право социального обеспечения.docx

• Музыка в сопи.docx

• 1 Конвективный способ.docx

• Лабораторная работа 11 (5) определение момента инерции колеса и момента силы трения.docx