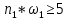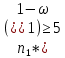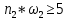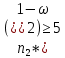Случай 1: генеральные дисперсии известны (z-тест)

1. 
   Найдем наблюдаемое значение критерия. Найдем точечные оценки мат ожидания (генеральные средние). При достаточно больших объемах выборок (≥30) выборочные средние имеют приближенно нормальный закон распределения, поэтом при выполнении H0 статистика z имеет стандартный нормальный закон распределения, т.е. формула (1):
   

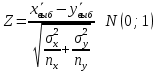
По формуле (1) находим наблюдаемое значение критерия.

2. 
   Найдем критические точки и критическую область S. Критическая область зависит от типа альтернативной гипотезы H1.
   
   1. 
      Н1 – двусторон. S-двусторон. Найдем 2 симметричные критические точки:
      

Zкр.пр. – квантиль станд норм расп. Уровня 1-α/2 (=НОРМ.СТ.ОБР(1-α/2))

Zкр.лев. – квантиль станд норм расп уровня α/2(=-Zкр.пр.)

S=(-∞;Zкр.лев.)U(Zкр.пр.;+∞)

2. 
   Н1- правосторон S-правосторон. Найдем одну критическую точку (правую):
   

Zкр.пр. – квантиль станд норм расп уровня 1- α (=НОРМ.СТ.ОБР(1- α))

S=(Zкр.пр.; +∞)

3. 
   Принятие решения относительно нулевой гипотезы: Если zнабл принадлежит критической области, то H0 отклоняется в пользу H1. Иначе нет оснований отклонять Н0.
   

Замечание 1: Если в условии даны несгруппированные ряды, то Z-тест в Excel можно реализовать с помощью инструмента в пакете анализа «Двухвыборочный Z-тест для средних».

Замечание 2: Этот инструмент дает значение p-value только для односторонней Н1, поэтому если Н1-двусторон, то полученное p-value надо умножить на 2.
Случай 2: генеральные дисперсии неизвестны (t-тест – критерий Стьюдента)

1. 
   Найдем несмещенные точечные оценки генеральных средних и генеральных СКО.
   

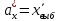
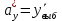
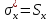
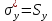
При условии выполнения H0, статистика t имеет распределение Стьюдента с k= 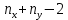степенями свободы, т.е. формула (2):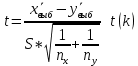



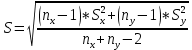– объединенная оценка СКО

По формуле (2) находим t набл

2. 
   Найдем критические точки и критическую область:
   
   1. 
      Н1 – двусторон. S- двусторон.
      

---

Найдем 2 симметричные критические точки.

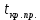- квантиль распределения Стьюдента уровня 1-α/2 (=СТЬЮДЕНТ.ОБР(1-α/2;k) =СТЬЮДЕНТ.ОБР.2Х(α;k))

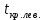- квантиль распределения Стьюдента уровня α/2 = -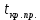

S=(-∞; 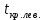)U( )

2. 
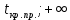   Н1-правосторон S-правосторон
   

Найдем одну критическую точку (правую)

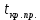- квантиль распределения Стьюдента уровня 1-α (=СТЬЮДЕНТ.ОБР(1-α;k) =СТЬЮДЕНТ.ОБР.ПХ(α;k)

S=( )

3. 
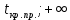   Принятие решения относительно нулевой гипотезы. Если наблюдаемое значение t принадлежит критической области, то Н0 отклоняется в пользу Н1 на уровне значимости альфа, иначе нет оснований отклонять Н0.
   

Замечание 1: Описанный способ проверки с помощью объединенного двухвыборочного t-теста можно проводить только когда генеральные дисперсии совокупностей Х и У можно считать равными, поэтому перед проверкой H0 нужно сначала проверить гипотезу о равенстве генеральных дисперсий с помощью критерия Фишера (F-теста).

Замечание 2: Если в условии даны несгруппированные выборки, то проверку можно осуществить с помощью инструментов Excel:

• 
  Если Генеральные дисперсии можно считать равными, то используем «двухвыборочный t-тест с одинаковыми дисперсиями
  
• 
  Если генеральные дисперсии нельзя считать равными, то используем «двухвыборочный t-тест с различными дисперсиями» (!!!р-значение в этом случае считается неверно)
  

Замечание 3: Если не проводить проверку гипотезы о равенстве генеральных дисперсий (неизвестно равны они или нет), то t-тест можно реализовать с помощью функций Excel.

P-value:

• 
  =СТЬЮДЕНТ.ТЕСТ(МассивХ ; Массив У; Хвосты (1, если Н1 – односторонняя, 2, если двусторонняя); Тип (3))
  
• 
  =ТТЕСТ(аргументы те же)
  

Если р-значение меньше альфа, то Н0 отклоняется в пользу Н1, иначе нет оснований отклонять Н0.

30. 
    Гипотеза о равенстве дисперсий 2-х нормально распределенных генеральных совокупностей.
    

1. 
   Найдем наблюдаемое значение критерия:
   

Найдем точечные несмещенные оценки генеральных дисперсий (

---

)

Если Н0 выполняется, то F-статистика имеет распределение Фишера С k1,k2 степенями свободы, т.е. по формуле (3):



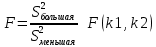
Где k1=n1-1 (n1- объем выборки с большей исправленной выб дисперсией), k2=n2-1 (n2 – объем выборки с меньшей исп выб дисп)

По формуле (3) найдем наблюдаемое значение критерия.

2. 
   Найдем критические точки и критическую область
   

• 
  Если Н1 двусторон, то S- двусторон.
  

F≥0, найдем 2 критические точки.

Fкр.лев. – квантиль распределения Фишера уровня α/2 (=F.ОБР(α/2;k1;k2) <1

Fкр.пр – квантиль распределения Фишера уровня 1- α/2 (=F.ОБР(1- α/2;k1;k2) >1

S=(0;Fкр.лев)U(Fкр.пр.;+∞)

• 
  Если Н1 правосторон, то S-правосторон
  

F≥0, найдем Fкр пр

Fкр.пр – квантиль распределения Фишера уровня 1-α (=F.ОБР(1- α;k1;k2); =F.ОБР.ПХ(α;k1;k2))

S=(Fкр.пр;+∞)

3. 
   Принятие решения относительно Н0: Если наблюдаемое значение принадлежит критической области, то Н0 отклоняется в пользу Н1, иначе нет оснований отклонять Н0.
   

Замечание: По несгруппированным выборкам F- тест можно провести следующими способами:

• 
  С помощью инструмента надстройки анализа данных «двухвыборочный F-тест для дисперсий»:
  
  • 
    Первый массив нужно ввести массив с наибольшей исп выб дисп
    
  • 
    Если Н1 односторонняя, то в строку «Альфа» вводим значение α, если двусторонняя, то α/2
    
  • 
    Этот инструмент считает р-значение для односторонней Н1, если Н1-двусторонняя, то р-значение надо умножить на 2
    
• 
  С помощью функции =F.ТЕСТ(Массив1;Массив2) – считает р-значение только для двусторонней Н1, если Н1 односторонняя, то значение надо разделить на 2.
  

31. 
    Гипотеза о равенстве генеральный долей признака в двух совокупностях.
    

Сравнение вероятностей успеха в двух сериях испытания Бернулли (z-тест)

Имеется 2 выборки, распределенные по биномиальному закону с параметрами (ni; pi), где pi- вероятность успеха в одном испытании Бернулли.

Проверка:

1. 
   Найдем наблюдаемое значение критерия.
   

По выборкам А:n1;k1, где k1 – число элементов с признаком и Б:n2;k2. n1 и n2 ≥30. Найдем несмещенные точечные оценки генеральных долей, т.е. выборочные доли:

---

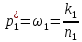
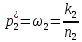
При достаточно больших объемах выборок выборочные доли имеют приближенно нормальный закон распределения. При условии, что Н0 выполняется Z-статистика имеет стандартное нормальное распределение, т.е. по формуле (4):



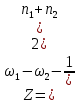
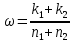– общая доля из двух выборок

.

2. 
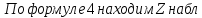   Найдем критические точки и критическую область
   

• 
  Если Н1 –двусторон, S- двусторон,
  

Найдем 2 симметричные критические точки

Zкр.пр. – квантиль станд норм расп уровня 1-α/2 (=НОРМ.СТ.ОБР(1-α/2))

Zкр.лев. – квантиль станд норм расп уровня α/2 (-Zкр.пр.)

S(-∞;Zкр.лев)U(Zкр.пр.;+∞)

• 
  Если Н1 – правосторон, S – правосторон
  

Найдем Zкр пр

Zкр. Пр. – квантиль станд норм рас уровня 1-α (=НОРМ.СТ.ОБР(1-α))

S=(Zкр.пр.;+∞)

3. 
   Принятие решения
   

Замечание: Z-тест можно использовать только при больших объемах выборки, т.е. когда выборки по объему репрезентативны (представительны):

• 
  
  
• 
  
  
• 
  
  
• 
  
  

Должны выполняться все 4 условия

32. 
    Гипотезы о числовых значениях параметров распределения.
    

33. 
    Суть и схема применения критерия согласия Пирсона.
    

0>2>0>

---

Смотрите также файлы

• Возможно ли привлечение Сапожникова к административной ответственности.doc

• Мдк. 01. 01 Право социального обеспечения.docx

• Музыка в сопи.docx

• 1 Конвективный способ.docx

• Лабораторная работа 11 (5) определение момента инерции колеса и момента силы трения.docx