ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 165
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Постоянная времени Т представляет собой интервал времени, в течение которого выходная величина достигла бы своего нового установившегося значения, если бы она изменялась с постоянной скоростью, равной скорости её изменения в начальный момент времени после поступления на вход единичного входного сигнала.
Чем >Т тем медленнее переходный процесс. Теоретически, переходный процесс в апериодическом звене длится бесконечно долго.
Под временем переходного процесса понимают промежуток времени, по истечении которого входная величина достигнет 0,95 от установившегося значения.
При t=3T
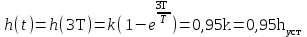 , т.е
, т.е 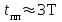 .
.При t=T
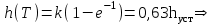
Т можно определить как время, за которое входная величина изменяясь от 0 достигла 0,63 от установившегося значения, при подаче на вход звена единичного ступенчатого воздействия.
Для весовой функции при t=T:
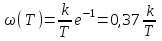 .
.Получим частотные характеристики звена.
КЧХ:
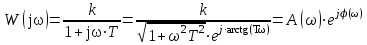
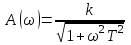 - АЧХ
- АЧХ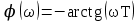 - ФЧХ
- ФЧХ-
Апериодическое звено 2-го порядка
Дифференциальное уравнение звена имеет вид:
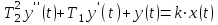
Операторное уравнение:
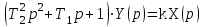
Разложим левую часть на множители:
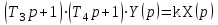 , где
, где 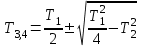 и Т4>Т3
и Т4>Т3Тогда передаточная функция звена:
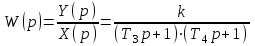
 (1)
(1)Очевидно, что Т3, Т4 могут быть как вещественными, так и комплексными.
При
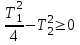 ;
;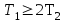 , корни будут вещественными, звено апериодическим 2-го порядка
, корни будут вещественными, звено апериодическим 2-го порядка
.
При
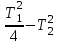 <0; Т1<2Т2, корни будут комплексными, звено колебательным.
<0; Т1<2Т2, корни будут комплексными, звено колебательным.При Т1=0 корни будут мнимыми, звено консервативным.
Из выражения (1) следует, что апериодическое звено 2-го порядка эквивалентно двум апериодическим звеньям 1-го порядка, соединённым последовательно.
Переходная функция звена:
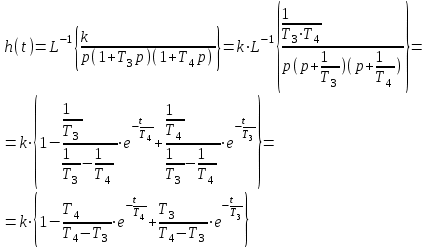
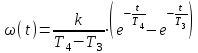
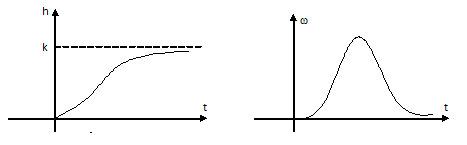
Рис. 9.6. Временные характеристики апериодического звена 2-го порядка
Получим частотные характеристики:
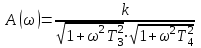
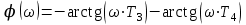
-
Колебательное звено
Дифференциальное уравнение звена такое же как и у апериодического 2-го порядка:
 .
.
Рис. 9.8. Примеры колебательных звеньев:
а) R,L,C – колебательный контур;б) механическая система ( m – масса;с – коэффициент упругости пружины;λ – коэффициент демфирования).
Характеристическое уравнение звена:
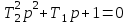
при
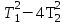 <0 или Т1<2Т2. В этом случае отношение
<0 или Т1<2Т2. В этом случае отношение 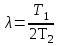 называют постоянной затухания ( коэффициент демпфирования) колебательного звена.
называют постоянной затухания ( коэффициент демпфирования) колебательного звена.При
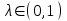 - колебательное звено; λ≥1 – апериодическое 2-го порядка; при λ=0 – консервативное.
- колебательное звено; λ≥1 – апериодическое 2-го порядка; при λ=0 – консервативное.Корни характеристического уравнения:
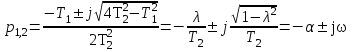
где
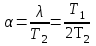 - коэффициент затухания;
- коэффициент затухания;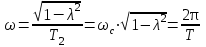 ;
;ω – частота собственных колебаний звена;
ωс=1/Т2 – угловая частота свободных колебаний при отсутствии затухания (λ=0).
Переходная функция колебательного звена:
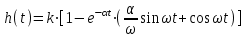
(2)
Весовая функция:
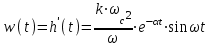 (3)
(3)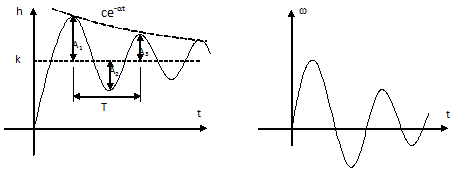
Рис. 9.9 Временные характеристики колебательного звена.
Уравнения (2), (3) характеризуют затухание во времени синусоидальных колебаний выходной величины с частотой
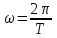 .Затухание этих колебаний определяется величиной коэффициента затухания α..
.Затухание этих колебаний определяется величиной коэффициента затухания α..Из рисунка 9.9 следует, что чем меньше α, тем больше колебательность переходного процесса.
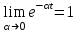
Колебательность можно оценивать по степени затухания Ψ, равной отношению разности двух соседних положительных амплитуд к большей из них (рис. 9.9):
 ,
,Из рисунка 9.9 =>
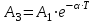 =>
=> 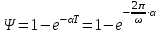 (4)
(4)Чем ближе к единице Ψ, тем быстрее затухают колебания переходного процесса.
Получим частотные характеристики звена:
КЧХ:
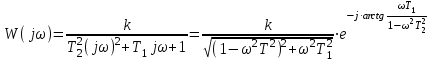
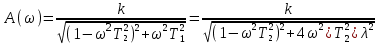
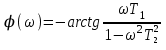
При
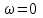 ;
; 
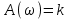
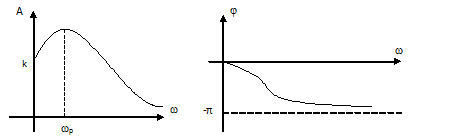
Рис. 9.10 Частотные характеристики звена АЧХ, ФЧХ
5. Консервативное звено
Консервативное звено является частным случаем колебательного звена.
При
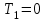 ,
, 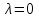 =>
=> 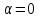 .
.Дифференциальное уравнение звена:
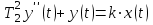
Тогда передаточная функция:
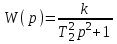 .
.Переходную функцию консервативного звена можно получить по переходной функции колебательного при
 ,
,  =>
=>  .
.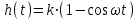
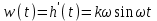
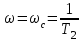
Рис. 9.12 Временные характеристики звена
КЧХ звена:
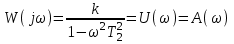
Рис. 9.13 Частотные характеристики
АФХ начинается на вещественной оси в точке
 и при подходе к частоте
и при подходе к частоте 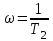 со стороны меньших значений уходит в бесконечность в положительном направлении вещественной оси. При дальнейшем увеличении частоты характеристика возвращается из бесконечности и стремится к началу координат слева.
со стороны меньших значений уходит в бесконечность в положительном направлении вещественной оси. При дальнейшем увеличении частоты характеристика возвращается из бесконечности и стремится к началу координат слева.Таким образом при
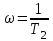 АЧХ имеет разрыв, который соответствует бесконечному возрастанию амплитуды, а ФЧХ скачком изменяет свое значение от 0 до –180°.
АЧХ имеет разрыв, который соответствует бесконечному возрастанию амплитуды, а ФЧХ скачком изменяет свое значение от 0 до –180°.§9.2 Интегрирующие звенья
1) Идеальное интегрирующее звено
Идеальное интегрирующее звено - это звено, в котором выходная величина пропорциональна интегралу входной величины.
Дифференциальное уравнение звена:
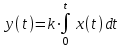 или
или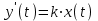 (1)
(1)где k – коэффициент передачи.
Коэффициент передачи идеального интегрирующего звена численно равен скорости изменения выходной величины при единичном значении входной. В этих случаях обычно пользуются не коэффицентом передачи, а величиной обратной ему, называемой постоянной времени интегрирования.
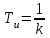 ,
,Если входная и выходная величина измеряются в одинаковых единицах, то
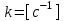
,
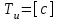 .
.Преобразуя (1) по Лапласу получим:
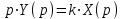 =>
=>Передаточная функция:
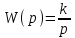
Переходная функция:
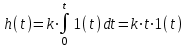
или
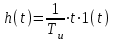 =>
=>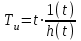
То есть постоянная времени интегрирования представляет собой интервал времени, в течение которого выходная величина достигнет входной.
Весовая функция:

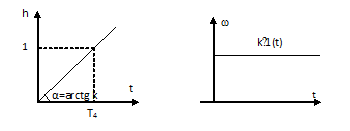
Рис. 9.15 Временные характеристики идеального интегрирующего звена
Комплексная передаточная функция звена:
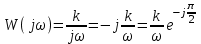 ;
;АЧХ:
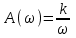 ВЧХ:
ВЧХ: 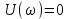
ФЧХ:
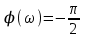 МЧХ:
МЧХ: 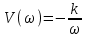 .
.2. Инерционное интегрирующее звено
Дифференциальное уравнение звена имеет вид:
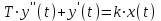
Передаточная функция звена:
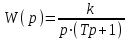
=> инерционное интегрирующее звено можно представить как совокупность последовательно включенных звеньев: идеального интегрирующего и апериодического 1-го порядка.
Для нахождения временных характеристик удобно воспользоваться формулой:
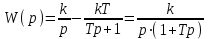
Переходная функция звена:
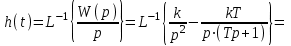
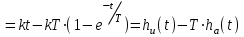
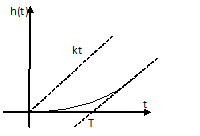
Рис. 9.17 Переходная функция инерционного интегрирующего звена