Файл: Основы автоматизации.docx

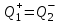(рисунок 11.2).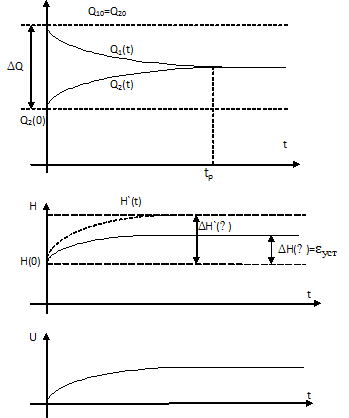


Рис. 11.2 Переходные процессы при П-регулировании

Однако регулируемая величина не вернется к заданному уровню – в системе будет постоянное по величине отклонение 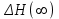, которое в общем случае называется установившейся (систематической) ошибкой .

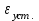Положительным фактором П-регулятора является его быстродействие. Из рисунка 11.2 следует, что использование П-регулятора привело к уменьшению остаточного отклонения по сравнению со случаем отсутсвия регулятора ( < ).
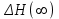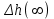§11.2 Интегральный регулятор

Регулятор, реализующий И-закон регулирования называется интегральным (И-регулятор). У И-регулятора изменение выходной величины (перемещение регулирующего органа) пропорционально интегралу от отклонения регулируемой величины. Уравнение динамики И-регулятора имеет вид:
u(t)= 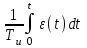или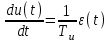

,

где 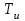- постоянная времени интегрирования, являющаяся настроечным параметром И-регулятора.

Из уравнения динамики следует, что скорость перемещения регулирующего органа пропорциональна величине рассогласования ε(t). Регулирующий орган будет перемещаться до тех пор, пока рассогласование (ошибка регулирования) не станет равным нулю: 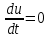(или u=const) при ε(t)=0.

Для И-регулятора характерно то, что при постоянно действующем возмущении он возвращает регулируемую величину к заданному значению, а следовательно устраняет ошибку системы:

---

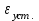
=0.

В динамическом отношении И-регулятор представляет собой идеальное интегрирующее звено с передаточной функцией

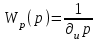
Рассмотрим реализацию И-закона на примере одноёмкостного объекта с самовыравниванием (рисунок 11.3).





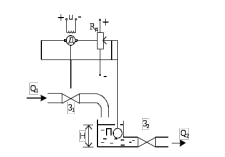
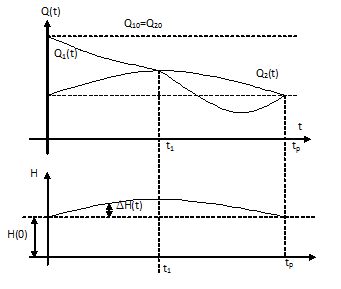
Рисунок 11.3 Пример реализации И-закона

В случае равенства уровень Н = Н(0), а поплавок П и задвижка З1 неподвижны. Движок потенциометрического датчика 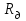находится посередине, напряжение питания якоря равно нулю. При уменьшении расхода жидкости на величину уровень жидкости в баке начнет расти, поплавок поднимется и перемещает вверх движок датчика. В цепи якоря ДПТ появляется напряжение U. Двигатель несколько закрывает задвижку З1 и приток жидкости Q1 уменьшается. В момент t1 величины Q1 и Q2 сравнялись (рисунок 11.3 б). Но так как уровень воды превышает заданный H(0), т.е. 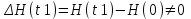, интеграл от рассогласования будет возрастать и следовательно регулирующее воздействие u(t) будет продолжать изменяться. В результате приток Q1 дополнительно уменьшится и станет меньше расхода Q2, поэтому уровень в баке начнет уменьшаться, что в свою очередь вызовет уменьшение расхода вытекающей жидкости Q2(t). В момент 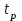приток и расход жидкости сравняются и уровень достигнет заданного значения H(0) (рисунок 11.3 в).

Процесс регулирования при И-законе прекратится, если одновременно будут выполнены 2 условия:

- уровень равен заданному H=H(0);

-приток жидкости равен расходу Q1=Q2.

Первое условие необходимо для того, чтобы регулирующее воздействие перестало изменяться. При выполнении второго условия в объекте достигается равновесие и уровень H постоянен. Эти условия выполняются, начиная с времени 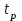, которое определяет время регулирования.

Сравнительный анализ П и И регуляторов

И-регулятор при постоянно действующем возмущении возвращает регулируемую величину к заданному значению, то есть устраняется ошибка регулирования

---

=0.(преимущество И-закона).

Однако при П-законе САР в переходном режиме будет иметь лучшие показатели качества, чем при И-законе регулирования (преимущество П-закона).


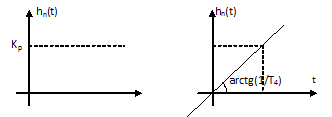
Рисунок 11.4 – Сравнение переходных характеристик П- и И-регуляторов.

В начальный момент времени П-регулятор сразу создает мощное регулирующее воздействие на объект. При И-законе, в начальный момент времени оно мало. Только спустя некоторое время воздействие И-регулятора достигает того же значения, что и при П-законе (рисунок 11.4).

Медленная реакция И-регулятора в начальный момент не позволяет достаточно эффективно компенсировать влияние возмущения на объект, поэтому в объекте при И- законе возникают более значительные динамические отклонения регулируемой величины, а сам процесс регулирования длится дольше.

Таким образом, П-регулирование обеспечивает хорошее свойство САР в переходном процессе, а И-регулирование позволяет полностью устранить ошибку регулирования.
§ 11.3 ПИ-регулятор

Регулятор, реализующий ПИ регулирование, называется пропорционально-интегральным регулятором (ПИ-регулятор). У ПИ-регулятора выходная величина изменяется под действием пропорциональной и интегральной составляющих, что обеспечивает наличие положительных
свойств, присущих П- и И-регуляторам.

Уравнение динамики ПИ-регулятора с независимыми параметрами настройки K_р и T_и:

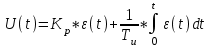(1)

В случае зависимых параметров настройки:

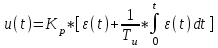(2)

В случае (1) величина называется постоянной интегрирования и представляет собой интервал времени, в течение которого интегральная составляющая выходной величины достигает значения входной.

Пусть ε(t)=1(t), тогда из (1) получаем .

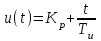При t= второе слагаемое равно единице, то есть входной величине ε(t).

Регулирующее воздействие:

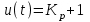(рисунок 11.5).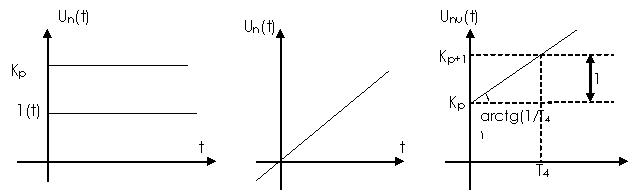

---

Рисунок 11.5 Составляющие переходных характеристик П-, И-, ПИ-регуляторов.

В случае (2) постоянная называется постоянной времени изодрома и иногда обозначается .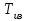

Пусть ε(t)=1(t), тогда по выражению (2)

.

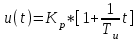При t=

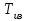
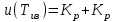=2 .

То есть при t= действие обоих составляющих одинаково и равно .

Постоянная времени изодрома численно равна интервалу времени, в течение которого регулирующее воздействие изменяется на величину, равную первоначальному изменению за счет пропорциональной составляющей, т.е. увеличивается в 2 раза.



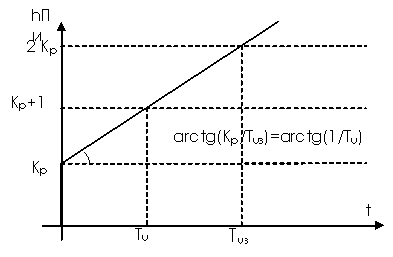
Рисунок 11.6- Переходная характеристика ПИ-регулятора.

В начале переходного процесса в ПИ-регуляторе мгновенно срабатывает пропорциональная (статическая часть), а за тем воздействие на объект постепенно увеличивается за счет интегральной части регулятора, называемой астатической.

Наиболее часто применяется изодромный регулятор, поэтому рассмотрим его свойства:

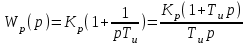(3)

КЧХ регулятора:
.

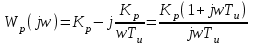АЧХ : .

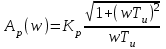ФЧХ: .

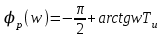ВЧХ: 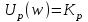; МЧХ: .



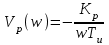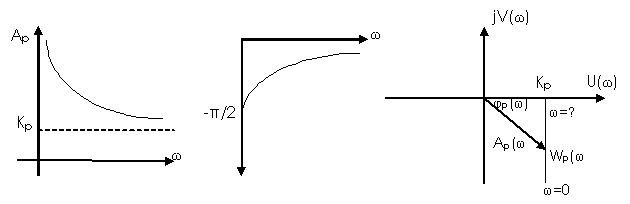
Рисунок 11.7 - Частотные характеристики ПИ-регулятора

ЛАХ регулятора имеет наклон (-20);0 дб/дек.
§11.4 Пропорционально-дифференциальный (ПД-регулятор)

---

П-, И-, и ПИ-регуляторы не могут упреждать ожидаемые отклонения регулируемой величины, реагируя только на имеющиеся в данный момент времени нарушения технологического процесса .Если регулируемая величина начинает быстро отклоняться от заданного значения ,то это значит, что на объект поступили значительные возмущения и отклонение будет значительным .В этом случае желательно иметь регулятор ,который вырабатывал бы регулирующее воздействие, пропорционально скорости изменения регулируемой величины ,упреждая её отклонения.

В САР используется ПД-регуляторы , оказывающие воздействия на регулирующий орган пропорционально отклонению регулируемой величины и скорости изменения этого отклонения.

U(t)= * + * .

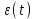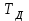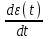Постоянная 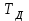называется постоянной времени дифференцирования и определяет величину регулирующего воздействия по производной от отклонения.

Рассмотрим переходную характеристику ПД- регулятора(рисунок 11.8).


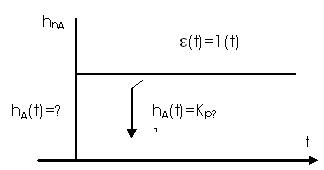
Рисунок 11.8 Переходная характеристика ПД-регулятора

При подаче на вход регулятора сигнала 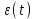=1(t) на выходе появится бесконечно большой сигнал от действия дифференциальной составляющей 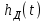= 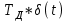и сигнал от пропорциональной составляющей 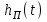= *1(t).Сигнал 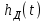сразу же падает до нуля , а сигнал 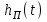остаётся постоянным и равным первоначальному.

Введение в закон регулирования производной по отклонению существенно повышает эффективность работы регулятора.

---