ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 167
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
20 и при отсутствии поступающей жидкости в бассейн (Q1 = 0). Аналогично молжно интерпретировать время заполнения бассейна (при Q2 = 0).
В связи с этим величина Тр называется временем разгона объекта. Очевидно, что Тр зависит от Н(0) и Q10.
В уравнении (3) коэффициент при переменной y(t) безразмерный. Он называется коэффициентом самовыравнивания объекта.
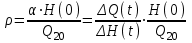 .
.
Объект лишен самовыравнивания, когда ρ = 0, если при неизменном значении расхода (ΔQ1(t) = 0), уровень воды изменяется ΔН(t)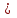 0.
0.
Учитывая введенные величины, уравнение (3) примет вид:
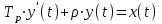 .
.
Для перехода к стандартной форме записи, поделим все члены уравнения на ρ:
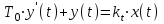 (4)
(4)
где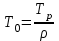 - постоянная времени объекта;
- постоянная времени объекта;
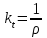 - коэффициент передачи объекта по возмущающему воздействию.
- коэффициент передачи объекта по возмущающему воздействию.
Уравнение (4) соответствует дифференциальному уравнению апериодического звена 1-го порядка. Поэтому рассматриваемый объект обладает динамическими характеристиками этого звена.
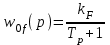 ;
; 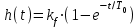 .
.
§ 10.2 Одноемкостный объект без самовыравнивания.
Примером такого объекта может служить бассейн, из которого вода отбирается не самотеком, а откачивается насосом постоянной производительностью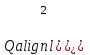 .
.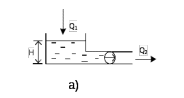
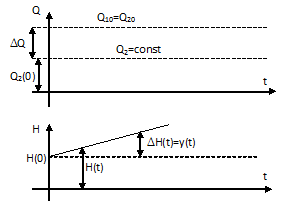
Рисунок 10.2 Одноёмкостный объект без самовыравнивания
В установившемся режиме:
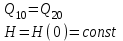
Нанесем объекту возмущение, уменьшив производительность насоса на величину , т.е.
, т.е. 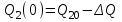
В результате разности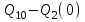
уровень воды в бассейне начнет возрастать. Т.к. производительность насоса не зависит от давления воды, то расход воды остается прежним: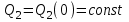
В переходном режиме:
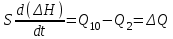
или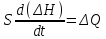
Очевидно, что у таких объектов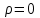 . Введя в рассмотрение те же величины, что и в предыдущем пункте, получим дифференциальное уравнение динамики объекта:
. Введя в рассмотрение те же величины, что и в предыдущем пункте, получим дифференциальное уравнение динамики объекта:
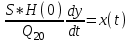 или
или
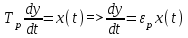 (1)
(1)
Величина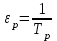 называется скоростью разгона и характеризуется скоростью изменения выходной величины при единичном входном воздействии. Для объекта без самовыравнивания скорость изменения регулируемой величины постоянна (рис. 2в).
называется скоростью разгона и характеризуется скоростью изменения выходной величины при единичном входном воздействии. Для объекта без самовыравнивания скорость изменения регулируемой величины постоянна (рис. 2в).
Временем разгона здесь будет время заполнения (до заданного значения уровня H(0)) пустого в начале бассейна, если расход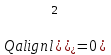 , а приток мгновенно изменится от 0 до
, а приток мгновенно изменится от 0 до 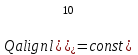 .
.
Очевидно, что уравнение динамики объекта соответствует уравнению идеального интегрирующего звена, поэтому его свойства будут присущи и рассматриваемому объекту.
Объекты, описываемые уравнением (1) называются одноемкостными объектами без самовыравнивания. Так как в переходном режиме все время сохраняется разница между притоком и расходом воды, то при любых возмущающих воздействиях регулируемая величина будет беспредельно (на практике до аварийного состояния) изменяться, а не стремиться к новому установившемуся значению. В связи с этим такие объекты не могут работать без принудительного регулирования.
Скорость изменения регулируемой величины в рассмотренном примере зависит от величины возмущающего воздействия и от площади поперечного сечения бассейна S. В данном случае S характеризует емкость объекта – его способность накапливать воду.
Передаточная функция объекта:
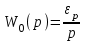 .
.
§10.3 Многоемкостные объекты с самовыравниванием
Эти объекты, также как и одноемкостные, обладают способностью самостоятельно приходить в новое состояние равновесия после нанесения им возмущения, однако переходные процессы в них отличаются от процессов в одноемкостных объектах.
Рассмотрим в качестве примера объект, состоящий из двух бассейнов, соединенных трубопроводом (рисунок 10.3).

Рисунок 10.3.1 Многоёмкостный объект с самовыравниванием
Регулируемая величина – уровень воды во втором бассейне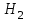 , а входная – изменение притока воды в 1-й бассейн
, а входная – изменение притока воды в 1-й бассейн 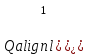 . Увеличим приток жидкости на входе, тогда начнет расти уровень воды в 1-м и во 2-м бассейнах.
. Увеличим приток жидкости на входе, тогда начнет расти уровень воды в 1-м и во 2-м бассейнах.
Однако изменение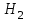 будет запаздывать относительно изменения
будет запаздывать относительно изменения 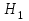 , т.к. при этом потребуется время на перетекание жидкости из 1-го бассейна во 2-й.
, т.к. при этом потребуется время на перетекание жидкости из 1-го бассейна во 2-й.
Такое запаздывание называется емкостным и зависит от сопротивления соединительного трубопровода.
Рассматриваемый объект можно рассматривать в виде последовательного соединения двух апериодических звеньев 1-го порядка.
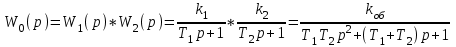 .
.
Таким образом, рассматриваемый объект подобен апериодическому звену 2-го порядка. После нанесения возмущения изменение регулируемой величины начинается с возрастающей, а затем с убывающей скоростью. Кривая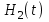 имеет точку перегиба, в которой скорость изменения регулируемой величины монотонна, с течением времени регулируемая величина стремится к установившемуся значению.
имеет точку перегиба, в которой скорость изменения регулируемой величины монотонна, с течением времени регулируемая величина стремится к установившемуся значению.
§10.4 Многоемкостные объекты без самовыравнивания.
Такие объекты, как и одноемкостные, после приложения к ним возмущения не приходят самостоятельно к состоянию равновесия. Свойства подобных объектовт рассмотрим на примере двухемкостного объекта (рис.10.5.1).
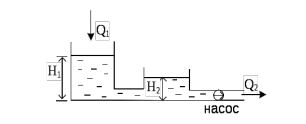
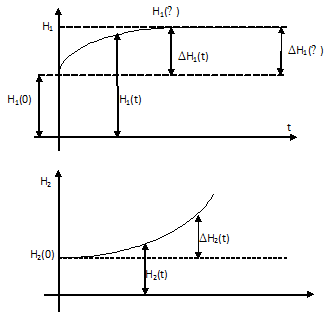
Рисунок 10.5.1 Многоёмкостный объект без самрвыравнивания
Регулируемой величиной является отклонение уровня воды во 2-м бассейне
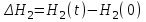 , а возмущающим воздействием – изменение притока
, а возмущающим воздействием – изменение притока 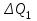 .
.
Такой объект можно представить в виде последовательного соединения апериодического звена 1-го порядка (1-й бассейн) с передаточной функцией:
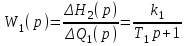 ,
,
и идеального интегрирующего звена (2-й бассейн) с передаточной функцией:
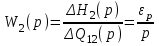 ,
,
где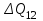 - приращение притока во 2-й бассейн.
- приращение притока во 2-й бассейн.
Передаточная функция объекта:
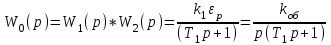
Таким образом, указанный объект в динамическом отношении подобен реальному интегрирующему звену.
Регулируемая величина не стремится к новому установившемуся значению.
§10.5 Объекты регулирования с запаздыванием
Все перечисленные объекты регулирования могут иметь транспортное запаздывание, при котором изменение регулируемой величины начинается спустя некоторое время τ после нанесения возмущения. В этом случае передаточная функция, полученная ранее, умножается на величину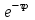 :
:
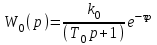
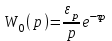 и т.д.
и т.д.
Переходные характеристики одноемкостных объектов с запаздыванием имеют вид (рисунок 10.5.1).
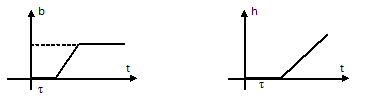
Рисунок 10.5.1 Переходные характеристики объектов с запаздыванием
§11. Законы регулирования и регуляторы
Будем считать, что на вход регулятора подается сигнал ошибки (рассогласование) между заданным и действительным значениями регулируемой величины (рис11.1) ε(t)=g(t)-y(t)
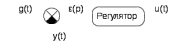
Рис. 11.1 Входные и выходные величины регулятора
Функциональная связь между выходной величиной регулятора (регулирующим воздействием) u(t) и его входной величиной ε(t) называется
законом регулирования.
На практике используют следующие типовые законы регулирования:
В этом случае регулирующее воздействие вырабатывается лишь в зависимости от величины и знака рассогласования:
u(t)=F[ε(t)].
2. Интегральный закон (И-закон):
u(t)= .
.
3. Пропорционально-интегральный закон (ПИ-закон):
u(t)=F[ε(t);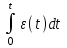 ].
].
u(t)=F[ε(t), ε’(t)].
5. Пропорционально-интергрально-дифференциальный (ПИД закон):
u(t)=F[ε(t),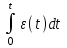 , ε’(t)].
, ε’(t)].
§ 11.1 Пропорциональный регулятор
Регулятор, реализующий П-закон регулирования называется пропорциональным (П-регулятор).
У идеального П-регулятора выходная величина в пределах зоны регулирования изменяется пропорционально изменению входной величины. Уравнение динамики идеального П-регулятора имеет вид:
u(t)=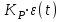 ,
,
где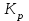 - коэффициент передачи регулятора.
- коэффициент передачи регулятора.
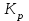 =
=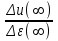 .
.
В динамическом отношении идеальный П-регулятор представляет пропорциональное(усилительное) звено с передаточной функцией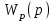 =
=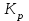 .
.
Рассмотрим особенности процесса регулирования при П-законе. В качестве объекта выберем одноемкостный объект с самовыравниваем рассмотренный ранее.
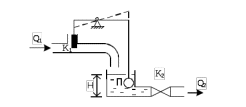
Рисунок 11.1 Пример реализации П-закона регулирования
Когда в бассейне произойдет отклонение уровня, регулятор тотчас же уменьшит на пропорциональную величину проходное отверстие регулирующего клапана К1.
Приток жидкости уменьшится, поэтому уровень будет расти с меньшей скоростью. Дальнейшее закрытие клапана и соответствующее уменьшение Q1 происходит по мере увеличения уровня жидкости. Баланс потоков жидкости достигается за счет совместного действия эффекта самовыравнивания (рост Q2) и уменьшения регулятором потока текущей жидкости Q1. Процесс регулирования закончится, когда установится равенство
В связи с этим величина Тр называется временем разгона объекта. Очевидно, что Тр зависит от Н(0) и Q10.
В уравнении (3) коэффициент при переменной y(t) безразмерный. Он называется коэффициентом самовыравнивания объекта.
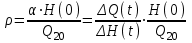 .
.Объект лишен самовыравнивания, когда ρ = 0, если при неизменном значении расхода (ΔQ1(t) = 0), уровень воды изменяется ΔН(t)
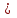 0.
0.Учитывая введенные величины, уравнение (3) примет вид:
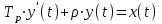 .
.Для перехода к стандартной форме записи, поделим все члены уравнения на ρ:
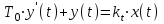 (4)
(4)где
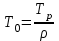 - постоянная времени объекта;
- постоянная времени объекта;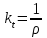 - коэффициент передачи объекта по возмущающему воздействию.
- коэффициент передачи объекта по возмущающему воздействию.Уравнение (4) соответствует дифференциальному уравнению апериодического звена 1-го порядка. Поэтому рассматриваемый объект обладает динамическими характеристиками этого звена.
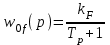 ;
; 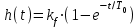 .
.§ 10.2 Одноемкостный объект без самовыравнивания.
Примером такого объекта может служить бассейн, из которого вода отбирается не самотеком, а откачивается насосом постоянной производительностью
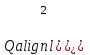 .
.

Рисунок 10.2 Одноёмкостный объект без самовыравнивания
В установившемся режиме:
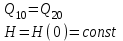
Нанесем объекту возмущение, уменьшив производительность насоса на величину
 , т.е.
, т.е. 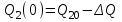
В результате разности
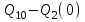
уровень воды в бассейне начнет возрастать. Т.к. производительность насоса не зависит от давления воды, то расход воды остается прежним:
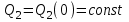
В переходном режиме:
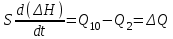
или
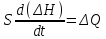
Очевидно, что у таких объектов
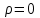 . Введя в рассмотрение те же величины, что и в предыдущем пункте, получим дифференциальное уравнение динамики объекта:
. Введя в рассмотрение те же величины, что и в предыдущем пункте, получим дифференциальное уравнение динамики объекта: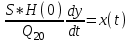 или
или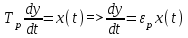 (1)
(1)Величина
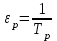 называется скоростью разгона и характеризуется скоростью изменения выходной величины при единичном входном воздействии. Для объекта без самовыравнивания скорость изменения регулируемой величины постоянна (рис. 2в).
называется скоростью разгона и характеризуется скоростью изменения выходной величины при единичном входном воздействии. Для объекта без самовыравнивания скорость изменения регулируемой величины постоянна (рис. 2в).Временем разгона здесь будет время заполнения (до заданного значения уровня H(0)) пустого в начале бассейна, если расход
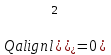 , а приток мгновенно изменится от 0 до
, а приток мгновенно изменится от 0 до 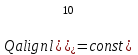 .
.Очевидно, что уравнение динамики объекта соответствует уравнению идеального интегрирующего звена, поэтому его свойства будут присущи и рассматриваемому объекту.
Объекты, описываемые уравнением (1) называются одноемкостными объектами без самовыравнивания. Так как в переходном режиме все время сохраняется разница между притоком и расходом воды, то при любых возмущающих воздействиях регулируемая величина будет беспредельно (на практике до аварийного состояния) изменяться, а не стремиться к новому установившемуся значению. В связи с этим такие объекты не могут работать без принудительного регулирования.
Скорость изменения регулируемой величины в рассмотренном примере зависит от величины возмущающего воздействия и от площади поперечного сечения бассейна S. В данном случае S характеризует емкость объекта – его способность накапливать воду.
Передаточная функция объекта:
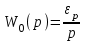 .
.§10.3 Многоемкостные объекты с самовыравниванием
Эти объекты, также как и одноемкостные, обладают способностью самостоятельно приходить в новое состояние равновесия после нанесения им возмущения, однако переходные процессы в них отличаются от процессов в одноемкостных объектах.
Рассмотрим в качестве примера объект, состоящий из двух бассейнов, соединенных трубопроводом (рисунок 10.3).

Рисунок 10.3.1 Многоёмкостный объект с самовыравниванием
Регулируемая величина – уровень воды во втором бассейне
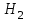 , а входная – изменение притока воды в 1-й бассейн
, а входная – изменение притока воды в 1-й бассейн 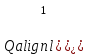 . Увеличим приток жидкости на входе, тогда начнет расти уровень воды в 1-м и во 2-м бассейнах.
. Увеличим приток жидкости на входе, тогда начнет расти уровень воды в 1-м и во 2-м бассейнах.Однако изменение
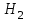 будет запаздывать относительно изменения
будет запаздывать относительно изменения 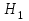 , т.к. при этом потребуется время на перетекание жидкости из 1-го бассейна во 2-й.
, т.к. при этом потребуется время на перетекание жидкости из 1-го бассейна во 2-й.Такое запаздывание называется емкостным и зависит от сопротивления соединительного трубопровода.
Рассматриваемый объект можно рассматривать в виде последовательного соединения двух апериодических звеньев 1-го порядка.
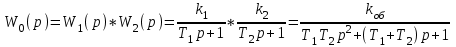 .
.Таким образом, рассматриваемый объект подобен апериодическому звену 2-го порядка. После нанесения возмущения изменение регулируемой величины начинается с возрастающей, а затем с убывающей скоростью. Кривая
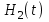 имеет точку перегиба, в которой скорость изменения регулируемой величины монотонна, с течением времени регулируемая величина стремится к установившемуся значению.
имеет точку перегиба, в которой скорость изменения регулируемой величины монотонна, с течением времени регулируемая величина стремится к установившемуся значению.§10.4 Многоемкостные объекты без самовыравнивания.
Такие объекты, как и одноемкостные, после приложения к ним возмущения не приходят самостоятельно к состоянию равновесия. Свойства подобных объектовт рассмотрим на примере двухемкостного объекта (рис.10.5.1).


Рисунок 10.5.1 Многоёмкостный объект без самрвыравнивания
Регулируемой величиной является отклонение уровня воды во 2-м бассейне
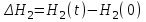 , а возмущающим воздействием – изменение притока
, а возмущающим воздействием – изменение притока 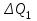 .
.Такой объект можно представить в виде последовательного соединения апериодического звена 1-го порядка (1-й бассейн) с передаточной функцией:
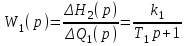 ,
,и идеального интегрирующего звена (2-й бассейн) с передаточной функцией:
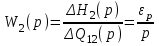 ,
,где
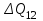 - приращение притока во 2-й бассейн.
- приращение притока во 2-й бассейн.Передаточная функция объекта:
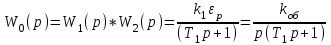
Таким образом, указанный объект в динамическом отношении подобен реальному интегрирующему звену.
Регулируемая величина не стремится к новому установившемуся значению.
§10.5 Объекты регулирования с запаздыванием
Все перечисленные объекты регулирования могут иметь транспортное запаздывание, при котором изменение регулируемой величины начинается спустя некоторое время τ после нанесения возмущения. В этом случае передаточная функция, полученная ранее, умножается на величину
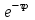 :
: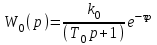
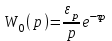 и т.д.
и т.д.Переходные характеристики одноемкостных объектов с запаздыванием имеют вид (рисунок 10.5.1).
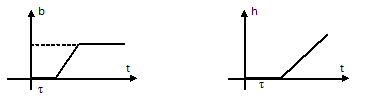
Рисунок 10.5.1 Переходные характеристики объектов с запаздыванием
§11. Законы регулирования и регуляторы
Будем считать, что на вход регулятора подается сигнал ошибки (рассогласование) между заданным и действительным значениями регулируемой величины (рис11.1) ε(t)=g(t)-y(t)
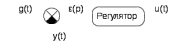
Рис. 11.1 Входные и выходные величины регулятора
Функциональная связь между выходной величиной регулятора (регулирующим воздействием) u(t) и его входной величиной ε(t) называется
законом регулирования.
На практике используют следующие типовые законы регулирования:
-
Пропорциональный закон(П-закон).
В этом случае регулирующее воздействие вырабатывается лишь в зависимости от величины и знака рассогласования:
u(t)=F[ε(t)].
2. Интегральный закон (И-закон):
u(t)=
 .
.3. Пропорционально-интегральный закон (ПИ-закон):
u(t)=F[ε(t);
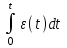 ].
].-
Пропорционально-дифференциальный закон (ПД-закон):
u(t)=F[ε(t), ε’(t)].
5. Пропорционально-интергрально-дифференциальный (ПИД закон):
u(t)=F[ε(t),
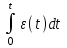 , ε’(t)].
, ε’(t)].§ 11.1 Пропорциональный регулятор
Регулятор, реализующий П-закон регулирования называется пропорциональным (П-регулятор).
У идеального П-регулятора выходная величина в пределах зоны регулирования изменяется пропорционально изменению входной величины. Уравнение динамики идеального П-регулятора имеет вид:
u(t)=
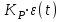 ,
,где
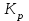 - коэффициент передачи регулятора.
- коэффициент передачи регулятора. 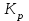 =
=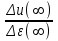 .
.В динамическом отношении идеальный П-регулятор представляет пропорциональное(усилительное) звено с передаточной функцией
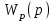 =
=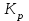 .
.Рассмотрим особенности процесса регулирования при П-законе. В качестве объекта выберем одноемкостный объект с самовыравниваем рассмотренный ранее.

Рисунок 11.1 Пример реализации П-закона регулирования
Когда в бассейне произойдет отклонение уровня, регулятор тотчас же уменьшит на пропорциональную величину проходное отверстие регулирующего клапана К1.
Приток жидкости уменьшится, поэтому уровень будет расти с меньшей скоростью. Дальнейшее закрытие клапана и соответствующее уменьшение Q1 происходит по мере увеличения уровня жидкости. Баланс потоков жидкости достигается за счет совместного действия эффекта самовыравнивания (рост Q2) и уменьшения регулятором потока текущей жидкости Q1. Процесс регулирования закончится, когда установится равенство