Файл: Основы автоматизации.docx

Весовая функция:





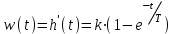
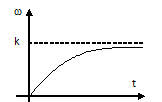
Рис. 9.18 Весовая функция звена.

Комплексная ПФ:


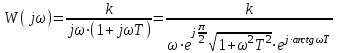
АЧХ:

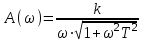
ФЧХ:


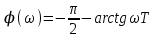
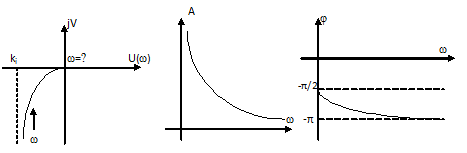
Рис. 9.19 АФХ, АЧХ, ФЧХ звена

3. Изодромное звено

Дифференциальное уравнение имеет вид:



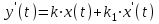
Передаточная функция:



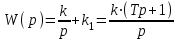
где T= k₁/k – постоянная времени изодромного звена.

Данное звено можно представить в виде параллельного соединения идеального интегрирующего и усилительного звеньев.

Переходная функция:

h(t) = L^-1{k/p²+ k₁/p} =

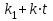
Весовая функция:

ω(t) = h’(t) = k


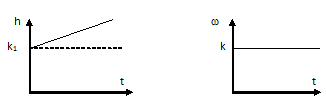
Рис. 9.21 Временные характеристики изодромного звена

Комплексная передаточная функция:

,

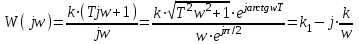Отсюда ВЧХ: U(ω) = k₁ ; МЧХ:V(ω) = -k/ω;

АЧХ: 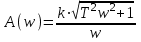; ФЧХ: .


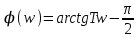Рис. 9.22 АФХ, АЧХ, ФЧХ звена
§ 9.3 Дифференцирующие звенья

1. Идеальное дифференцирующее звено

Идеальное дифференцирующее звено – это звено у которого величина на выходе пропорциональна скорости изменения входной величины.

Дифференциальное уравнение звена:

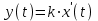(1)

Передаточная функция:



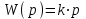
Переходная функция звена:



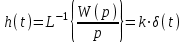
Весовая функция:



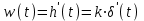
δ’(t) можно представить в виде прямоугольных, достаточно узких и противоположных по знаку импульса, расположенных по разные стороны от точки t = 0 и стремящиеся по длительности и к 0.

---

Комплексная передаточная функция:



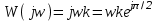
Тогда АЧХ: A(ω) = kω; ФЧХ: φ(ω) = π/2; ВЧХ: U(ω) = 0; МЧХ: V(ω) = ωk.

Асимптотическая ЛАХ звена:

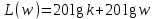(+20 дБ/дек).

2. Инерционное дифференцирующее звено

Дифференциальное уравнение звена:

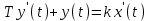(1)

Передаточная функция:



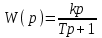
Реальное (инерционное) дифференцирующее звено можно представить в виде последовательного соединения идеального дифференцирующего звена и апериодического звена 1 порядка.

Переходная функция звена:

.

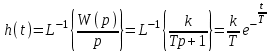Весовая функция:

.

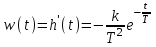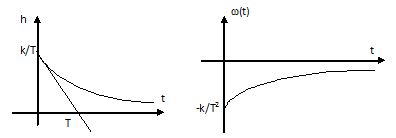
Рисунок 9.24 Временные характеристики звена

Частотные характеристики звена:

Комплексная передаточная функция:

.

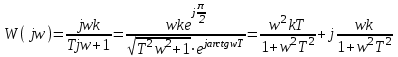Отсюда

АЧХ: 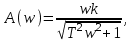ФЧХ: φ(ω) = π/2 – arctg(ωT) ;

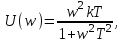ВЧХ: МЧХ: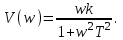

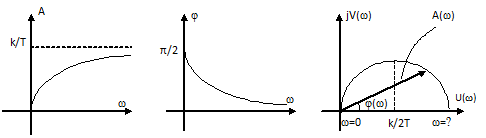
Рисунок 9.25 Частотные характеристики звена

Из уравнения ФЧХ видно, что реальное дифференцирующее звено создает опережение выходных колебаний по отношению ко входным тем меньше, чем больше частота колебаний.

Из графика АФХ видно, что вектор W(jω) при изменении частоты от 0 до постоянно увеличивается, а угол φ(ω) уменьшается от π/2 до 0

0>

---

§ 9.4 Звено запаздывания

На практике во многих устройствах имеется так называемое транспортное запаздывание, при котором выходная величина начинает изменяться через некоторый промежуток времени после начала изменения входной величины.

Уравнение звена имеет вид:



Тогда передаточная функция:

Y(p) = e^-τpX(p) => W(p) = e^-τp .

Переходная функция звена:

h(t) = 1(t – τ),

весовая функция:

ω(t) = δ(t – τ).

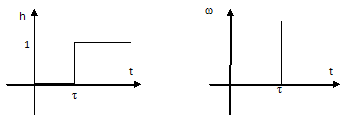
рис. 9.26 Временные характеристики звена.

Частотные характеристики:

W(jω) = e^-jωτ ;A(ω) = 1; φ(ω) = -ωτ; L(ω) = 0.


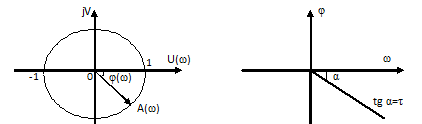
Рисунок 9.27 АФХ, ФЧХ звена.

АФХ представляет собой окружность радиуса R=1 и центром в начале координат. При w=0 вектор расположен положительной вещественной оси, с ростом частоты он поворачивается по часовой стрелке и при ω=2π/τ возвращается в исходное положение. При бесконечном увеличении частоты, вектор бесконечное число раз поворачивается вокруг начала координат.

§10. Типовые объекты регулирования и их свойства.

Объекты автоматического регулирования характеризуются некоторыми переменными и постоянными параметрами. Через объект непрерывно поступает вещество или энергия. В установившемся режиме приток вещества или энергии в объект равен расходу, в следствие чего регулируемая величина (температура, давление и т.д.) не изменяется. Если объект испытывает возмущающее воздействие, т.е. воздействие, нарушающее равенство притока и расхода вещества, регулируемая величина изменяется. Характер этого изменения зависит как от возмущающего воздействия так и от свойств объекта.

Количество вещества или энергии, содержащееся в объекте в данный момент времени называют ёмкостью объекта регулирования.

Ёмкость отражает способность объекта накапливать вещество или энергию и характеризует его инерционность.

Объект может обладать ёмкостью только при наличии в нём сопротивления выходу вещества или энергии.

---

Различают одноёмкостные и многоёмкостные объекты.

При всём многообразии ОР их так же, как и любые элементы САР можно классифицировать по динамическим свойствам и отнести либо к типовому динамическому звену, либо к комбинации таких звеньев.

Различают объекты с самовыравниванием (саморегулированием) и без самовыравнивания.

Самовыравнивание характеризует свойство ОР самостоятельно приходить к новому установившемуся режиму при ограниченном возмущающем воздействии.

Перечисленные ОР могут иметь запаздывания. Рассмотрим свойства ОР.


10.1. Одноёмкостный объект с самовыравниванием

Примером такого ОР может служить бассейн, показанный на рисунке 10.1.




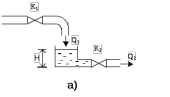
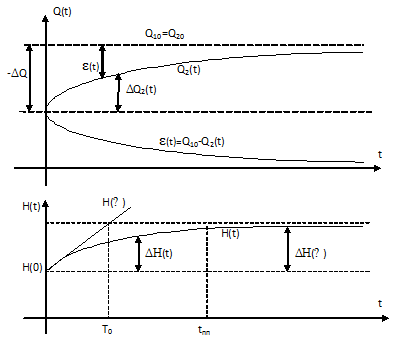
Рисунок 10.1 – Одноёмкостный объект с самовыравниванием

В бассейн непрерывно подаётся вода в количестве 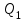м3/мин, и также непрерывно отбирается для производственных нужд в количестве 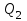м3/мин. Выходная (регулируемая) величина – уровень Н воды, который необходимо поддерживать в заданных пределах.

Установившийся режим:

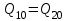Приток воды = Расходу

Н = Н(0) = const

Нанесём объекту возмущение, резко уменьшив расход воды клапаном 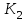на величину .

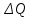Расход воды станет равным:



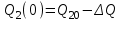
Поскольку расход стал меньше притока, уровень воды в бассейне начнёт возрастать (рис10.1в). Увеличение столба жидкости ведёт к повышению давления на выходе из бассейна, поэтому расход Q2 будет увеличиваться по мере роста уровня.



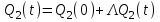
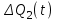– зависит от Н(t).

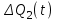– приращение расхода (рис. 10.1.б).

Когда расход

---

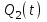достигнет значения притока 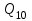, изменение выходной величины Н закончится и наступит новый установившийся режим, которому соответствует Н( ) (рис.10.1.в).

Для малых изменений уровня можно приближённо считать, что изменение расхода воды пропорционально изменению уровня:

,

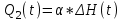Где 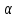– постоянный коэффициент (м2/мин), зависящий от свойств объекта.

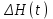= Н(t) – Н(0) – приращение уровня.

Получим дифференциальное уравнение ОР, используя уравнение материального баланса (закон сохранения вещества и энергии).



Закон сохранения вещества (или энергии):

Накопление вещества = приток – расход.

За время Δt объем воды в бассейне возрастет на величину:

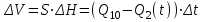(1)

S – площадь поперечного сечения бассейна. По графику (рис 10.1.б) видно что:

Q₁₀ – Q₂(t) = ΔQ – ΔQ₂(t)

То есть



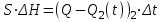
При малых приращениях и учитывая , что :

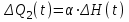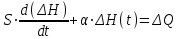(2)

Все члены этого уравнения имеют определенную размерность. Для анализа динамических свойств ОР перейдем к уравнению в относительных единицах. Для этого введем следующие обозначения:

,

,

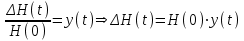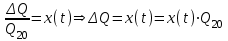Здесь в качестве базовых величин приняты значения при установившемся режиме Н(0) и Q₂₀. Тогда уравнение (2) примет вид:

,

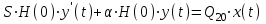Поделим обе части на Q₂₀

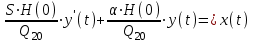(3)

Нетрудно видеть, что коэффициент при производной:

( )

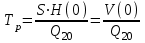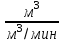равен времени, необходимому для полного опустошения бассейна от номинального уровня Н(0) с постоянной скоростью, при значении расхода Q

---