Файл: Методические указания и контрольные задания для студентовзаочников инженернотехнических и технологических специальностей вузов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 249
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Дано: т—0,01 кг, Т= 1 с, Е=0,02 Дж.
Н аи ТИ. A, Дгтит»
Решение. Уравнение гармонического колебания имеет вид
s=A sin фо)> (1)
где s — смещение материальной точки от положения равновесия, А — амплитуда колебания, со — циклическая частота, t — время, сро — начальная фаза.
Скорость материальной точки определяется как первая производная от смещения по времени:
ds
Полная энергия колебания складывается из кинетической и потенциальной энергии и равна максимальной кинетической или максимальной потенциальной энергии:
„ то)2А2
(6)
Из этого выражения найдем амплитуду колебания

Произведем вычисления, учитывая, что циклическая частота и период колебаний связаны соотношением
2я 2 • 3,14 ,
со=—= = 6,28 с
Т 1с
л 1 /2 0,02 Дж л
А= / — = 0,32 м;
6,28 с-1 v 0,01 кг
Чп«=6,28 с'1 • 0,32 м=2 м/с;
Отах = (6,28 с-1)2 ’ 0,32 м=12,6 м/с2.
Ответ-. Л=0,32 м, vmax=2 м/с, атах=12,6 м/с2.
Дано: Нт=0,1 А/т, S'=l м2, /= 1 с, T«t, е=1, д = 1.
Найти: И7.
Решение. Плотность потока энергии электромагнитной волны определяется вектором Пойнтинга
р=ЕхН, (1)
где Е и Н — векторы напряженности электрического и магнитного полей. Учитывая, что векторы Е и Н электромагнитной волны взаимно перпендикулярны, для модуля вектора р получим р=ЕН. (2)
Так как величины Е и Н в каждой точке волны меняются со временем по гармоническому закону, находясь в одинаковых фазах, то мгновенное значение р равно
р = Ет sin art • Нт sin art = ЕтНт sin2 со/. (3)

dlF
d/
Энергия, переносимая через площадку S', перпендикулярную направлению распространения волны, в единицу времени,

(4)
(5)
р dS=PS — SEmHm sin2 со/.
s
Учитывая, что в электромагнитной волне
; £ое£2=; ДоД/ZL 2 2
найдем:
I или
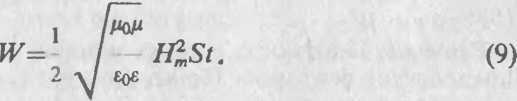
Подставляя числовые значения, получим
71ё !о-т Гн/м • 1 ' (0>1 А/М)2 ■ 1 м2 1 с= *’88 Дж-
Ответ: ^=1,88 Дж.
Дано: и = 1,25, 2=0,72 мкм, z=60°.
Найти: d^.
Решение. Оптическая разность хода лучей, отраженных от нижней и верхней поверхности пленки, равна
A=2d ^/и2 —sin2i, (1)
где d — толщина пленки, п — показатель преломления пленки, i — угол падения лучей.
В выражении (1) учтено, что отражение лучей на обеих поверхностях происходит от оптически более плотной среды, и поэтому потери полуволны в обоих случаях компенсируют друг друга. Условие интерференционного минимума имеет вид 98
A = ±(2m- 1)Л/2, m= 1, 2, ..., (2)

(3)
где 2 — длина волны света. Подставляя (1) в (2) и учитывая, что выражение (1) положительно, получим 2d y/n2—sin2i =■ (2т —1)2/2.

(4)
Из (3) найдем возможные значения толщины пленки:
-
Материальная точка массой 10 г совершает гармоническое колебание с периодом 1 с. Определить амплитуду колебаний, максимальные скорость и ускорение колеблющейся точки, если полная энергия точки равна 0,02 Дж.
Дано: т—0,01 кг, Т= 1 с, Е=0,02 Дж.
Н аи ТИ. A, Дгтит»
Решение. Уравнение гармонического колебания имеет вид
s=A sin фо)> (1)
где s — смещение материальной точки от положения равновесия, А — амплитуда колебания, со — циклическая частота, t — время, сро — начальная фаза.
Скорость материальной точки определяется как первая производная от смещения по времени:
ds
Полная энергия колебания складывается из кинетической и потенциальной энергии и равна максимальной кинетической или максимальной потенциальной энергии:
„ то)2А2
(6)
Из этого выражения найдем амплитуду колебания
Произведем вычисления, учитывая, что циклическая частота и период колебаний связаны соотношением
2я 2 • 3,14 ,
со=—= = 6,28 с
Т 1с
л 1 /2 0,02 Дж л
А= / — = 0,32 м;
6,28 с-1 v 0,01 кг
Чп«=6,28 с'1 • 0,32 м=2 м/с;
Отах = (6,28 с-1)2 ’ 0,32 м=12,6 м/с2.
Ответ-. Л=0,32 м, vmax=2 м/с, атах=12,6 м/с2.
-
' В вакууме распространяется плоская электромагнитная волна. Амплитуда напряженности магнитного поля волны 0,1 А/м. Определить энергию, переносимую этой волной через поверхность площадью 1 м2, расположенную перпендикулярно направлению распространения волны, за время /=1 с. Период волны Т«1.
Дано: Нт=0,1 А/т, S'=l м2, /= 1 с, T«t, е=1, д = 1.
Найти: И7.
Решение. Плотность потока энергии электромагнитной волны определяется вектором Пойнтинга
р=ЕхН, (1)
где Е и Н — векторы напряженности электрического и магнитного полей. Учитывая, что векторы Е и Н электромагнитной волны взаимно перпендикулярны, для модуля вектора р получим р=ЕН. (2)
Так как величины Е и Н в каждой точке волны меняются со временем по гармоническому закону, находясь в одинаковых фазах, то мгновенное значение р равно
р = Ет sin art • Нт sin art = ЕтНт sin2 со/. (3)

dlF
d/
Энергия, переносимая через площадку S', перпендикулярную направлению распространения волны, в единицу времени,

(4)
(5)
р dS=PS — SEmHm sin2 со/.
s
Учитывая, что в электромагнитной волне
; £ое£2=; ДоД/ZL 2 2
найдем:
I или
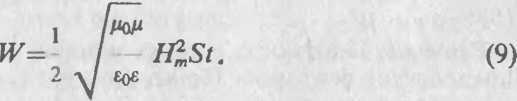
Подставляя числовые значения, получим
Ответ: ^=1,88 Дж.
-
Для устранения отражения света от поверхности линзы на нее наносится тонкая пленка вещества с показателем преломления 1,25, меньшим, чем у стекла (просветление оптики). При какой наименьшей толщине пленки отражение света с длиной волны 0,72 мкм не будет наблюдаться, если угол падения лучей 60°?
Дано: и = 1,25, 2=0,72 мкм, z=60°.
Найти: d^.
Решение. Оптическая разность хода лучей, отраженных от нижней и верхней поверхности пленки, равна
A=2d ^/и2 —sin2i, (1)
где d — толщина пленки, п — показатель преломления пленки, i — угол падения лучей.
В выражении (1) учтено, что отражение лучей на обеих поверхностях происходит от оптически более плотной среды, и поэтому потери полуволны в обоих случаях компенсируют друг друга. Условие интерференционного минимума имеет вид 98
A = ±(2m- 1)Л/2, m= 1, 2, ..., (2)

(3)
где 2 — длина волны света. Подставляя (1) в (2) и учитывая, что выражение (1) положительно, получим 2d y/n2—sin2i =■ (2т —1)2/2.

(4)
Из (3) найдем возможные значения толщины пленки: