Файл: Методические указания и контрольные задания для студентовзаочников инженернотехнических и технологических специальностей вузов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 254
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
45- По кольцевому проводнику радиусом 10 см течет ток 4 А. Параллельно плоскости кольцевого проводника на расстоянии
-
см над его центром проходит бесконечно длинный прямолинейный проводник, по которому течет ток 2 А. Определить индукцию и напряженность магнитного поля в центре кольца. Рассмотреть все возможные случаи.
-
Два круговых витка с током лежат в одной плоскости и имеют общий центр. Радиус большого витка 12 см, меньшего 8 см. Напряженность поля в центре витков равна 50 А/м, если токи текут в одном направлении, и нулю, если в противоположном. Определить силу токов, текущих по круговым виткам. -
Бесконечно длинный прямолинейный проводник с током
-
А расположен на расстоянии 20 см от центра витка радиусом 10 см с током 1 А. Определить напряженность и индукцию магнитного поля в центре витка для случаев, когда проводник: а) расположен перпендикулярно плоскости витка; б) в плоскости витка.
-
По квадратной рамке со стороной 0,2 м течет ток 4 А. Определить напряженность и индукцию магнитного поля в центре рамки. -
По квадратной рамке течет ток 4 А. Напряженность маг-
А
нитного поля в центре рамки 45 —. Определить периметр рамки, м
-
По квадратной рамке со стороной 0,2 м течет ток, который создает в центре рамки магнитное поле напряженностью 4,5 А/м. Определить силу тока в рамке. -
Незакрепленный проводник массой 0,1 г и длиной 7,6 см находится в равновесии в горизонтальном магнитном поле напряженностью 10 А/м. Определить силу тока в проводнике, если он перпендикулярен линиям индукции поля. -
Два параллельных бесконечно длинных проводника с токами 10 А взаимодействуют с силой 1 мН на 1 м их длины. На каком расстоянии находятся проводники? -
Найти радиус траектории протона в магнитном поле с индукцией 2,5 Тл, если он движется перпендикулярно ему и обладает кинетической энергией 3 МэВ. -
Какое ускорение приобретает проводник массой 0,1 г
и длиной 8 см в однородном магнитном поле напряженностью 10 кА/м, если сила тока в нем 1 А, а направления тока и индукции взаимно перпендикулярны? *
-
Электрон с энергией 300 эВ движется перпендикулярно линиям индукции однородного магнитного поля напряженностью 465 А/м. Определить силу Лоренца, скорость и радиус траектории электрона. -
Момент импульса протона в однородном магнитном поле напряженностью 20 кА/м равен 6,6 • 10“23 кг • м2/с. Найти кинетическую энергию протона, если он движется перпендикулярно линиям магнитной индукции поля. -
На расстоянии 5 мм параллельно прямолинейному длинному проводнику движется электрон с кинетической энергией 84
1 кэВ. Какая сила будет действовать на электрон, если по проводу пустить ток 1 А?
-
Протон движется в магнитном поле напряженностью 10 А/м по окружности радиусом 2 см. Найти кинетическую энергию протона. -
По прямолинейным длинным параллельным проводникам, находящимся на расстоянии 2 см, в одном направлении текут токи по 1 А. Какую работу на единицу длины проводников нужно совершить, чтобы раздвинуть их до расстояния 4 см? -
Однородное магнитное поле напряженностью 900 А/м действует на помещенный в него проводник длиной 25 см с силой 1 мН. Определить силу тока в проводнике, если угол между направлениями тока и индукции магнитного поля равен 45°. -
Перпендикулярно линиям индукции однородного магнитного поля индукцией 0,3 Тл движется проводник длиной 15 см со скоростью 10 м/с, перпендикулярной проводнику. Определить ЭДС, индуцируемую в проводнике. -
Перпендикулярно линиям индукции однородного магнитного поля индукцией 1 мТл по двум параллельным проводникам движется без трения перемычка длиной 20 см. При замыкании цепи, содержащей эту перемычку, в ней идет ток 0,01 А. Определить скорость движения перемычки. Сопротивление цепи 0,1 Ом. -
На концах крыльев самолета размахом 20 м, летящего со скоростью 900 км/ч, возникает электродвижущая сила индукции 0,06 В. Определить вертикальную составляющую напряженности магнитного поля Земли. -
В плоскости, перпендикулярной однородному магнитному полю напряженностью 2 • 105 А/м вращается стержень длиной 0,4 м относительно оси, проходящей через его середину. В стержне индуцируется электродвижущая сила, равная 0,2 В. Определить угловую скорость стержня. -
Катушка из 100 витков площадью 15 см2 вращается с частотой 5 Гц в однородном магнитном поле индукцией 0,2 Тл. Ось вращения перпендикулярна оси катушки и линиям индукции поля. Определить максимальную электродвижущую силу индукции в катушке. -
Цепь состоит из соленоида и источника тока. Соленоид без сердечника длиной 15 см и диаметром 4 см имеет плотную намотку из двух слоев медного провода диаметром 0,2 мм. По соленоиду течет ток 1 А. Определить ЭДС самоиндукции в соленоиде в тот момент времени после отключения его от источника тока, когда сила тока уменьшилась в два раза. Сопротивлением источника тока и подводящих проводов пренебречь. -
Решить задачу 66 для случая соленоида с сердечником, магнитная проницаемость которого равна 1000. -
Сила тока в соленоиде равномерно возрастает от 0 до 10 А за 1 мин, при этом соленоид накапливает энергию 20 Дж. Какая ЭДС индуцируется в соленоиде? -
Однослойный соленоид без сердечника длиной 20 см и диаметром 4 см имеет плотную намотку медным проводом диаметром 0,1 мм. За 0,1 с сила тока в нем равномерно убывает с 5 А до 0. Определить электродвижущую силу индукции в соленоиде. -
По условию задачи 69 определить заряд, прошедший через соленоид после его отключения. -
Чему равна объемная плотность энергии магнитного поля в соленоиде без сердечника, имеющего плотную однослойную намотку проводом диаметром 0,2 мм, если по нему течет ток величины 0,1 А? -
По условию задачи 71 найти энергию магнитного поля соленоида, если его длина 20 см, а диаметр 4 см. -
По соленоиду длиной 0,25 м, имеющему число витков 500,
течет ток 1 А. Плошадь поперечного сечения 15 см2. В соленоид вставлен железный сердечник. Найти энергию магнитного поля соленоида. Зависимость приведена на рис 4.
-
Квадратная рамка со стороной 1 см содержит 100 витков и помещена в однородное магнитное поле напряженностью 100 А/м. Направление поля составляет угол 30° с нормалью к рамке. Какая работа совершается при повороте рамки на 30° в одну и другую сторону, если по ней течет ток 1 А? -
По условию задачи 74 определить работу при повороте рамки в положение, при котором ее плоскость совпадает с направлением линий индукции поля. -
Под действием однородного магнитного поля перпендикулярно линиям индукции начинает перемещаться прямолинейный проводник массой 2 г, по которому течет ток 10 А. Какой магнитный поток пересечет этот проводник к моменту времени, когда скорость его станет равна 31,6 м/с? -
Проводник с током 1 А длиной 0,3 м равномерно вращается вокруг оси, проходящей через его конец, в плоскости, перпендикулярной линиям индукции магнитного поля напряженностью 1 кА/м. За одну минуту вращения совершается работа 0,1 Дж. Определить угловую скорость вращения проводника. -
Однородное магнитное поле, объемная плотность энергии которого 0,4 Дж/м3, действует на проводник, расположенный перпендикулярно линиям индукции, силой 0,1 мН на 1 см его длины. Определить силу тока в проводнике. -
По обмотке соленоида с параметрами: число витков — 1000, длина 0,5 м, диаметр — 4 см; течет ток 0,5 А. Зависимость B=f(H) для сердечника приведена на рис. 4. Определить потокосцепление, энергию и объемную плотность энергии соленоида. -
Обмотка соленоида имеет сопротивление 10 Ом. Какова его индуктивность, если при прохождении тока за 0,05 с в нем выделяется количество теплоты, эквивалентное энергии магнитного поля соленоида?
III. КОЛЕБАНИЯ. ВОЛНЫ. ОПТИКА
1 ... 4 5 6 7 8 9 10 11 12
ПОЯСНЕНИЯ К РАБОЧЕЙ ПРОГРАММЕ
При изучении темы «Колебания» следует параллельно рассматривать механические и электромагнитные колебания, что способствует выработке у студента единого подхода к колебаниям различной физической природы. Здесь следует четко уяснить понятия фазы, разности фаз, амплитуды, частоты, периода колебаний, и там, где это необходимо, использовать графический метод представления гармонического колебания. Нужно уяснить, что любые колебания линейной системы всегда можно представить в виде суперпозиции одновременно совершающихся гармонических колебаний с различными частотами, амплитудами и начальными фазами.
Изучение темы «Волны» целесообразно начинать с механических волн, распространяющихся в упругих средах. Здесь следует обратить внимание на картину мгновенного распределения смещений и скоростей в бегущей волне, различие между бегущей и стоячей волнами, зависимость фазовой скорости от частоты колебаний, найти связь между групповой и фазовой скоростями и показать их равенство в отсутствие дисперсии волн. Особое внимание студент должен уделить условию интерференции волн, энергетическому соотношению при интерференции волн, понять и объяснить перераспределение энергии при образовании минимумов и максимумов интенсивности. Переходя к изучению электромагнитных волн, студенту следует ясно представить себе физический смысл уравнений Максвелла и, опираясь на них, рассмотреть свойства этих волн. Нужно четко представлять, что переменные электрическое и магнитное поля взаимосвязаны, они поддерживают друг друга и могут существовать независимо от источника, их породившего, распространяясь в пространстве в виде электромагнитной волны. Другими словами, электромагнитная волна — это распространяющееся в пространстве переменное электромагнитное поле. Под энергией электромагнитного поля следует подразумевать сумму энергий электрического и магнит- 88
ного полей. Простейшей системой, излучающей электромагнитные волны, является колеблющийся электрический диполь. Следует помнить, что если диполь совершает гармонические колебания, то он излучает монохроматическую волну.
В настоящее время волновая оптика является частью общего учения о распространении волн. При изучении явлений интерференции, дифракции, объясняемых с позиций волновой природы света, студент должен обратить внимание на общность этих явлений для волн любой природы. Но световые волны имеют специфические особенности, когерентность, монохроматичность, которые обусловлены конечной длительностью свечения отдельного атома.
При изучении интерференции света особое внимание следует обратить на такие вопросы, как цвета тонких пленок, полосы равной толщины и равного наклона. Следует помнить, что при интерференции света имеет место суперпозиция, связанная с перераспределением энергии, а не с взаимодействием волн.
Рассматривая явление дифракции, необходимо уяснить метод зон Френеля, уметь пользоваться графическим методом сложения амплитуд, что будет способствовать пониманию дифракции на одной щели, дифракционной решетке. Кроме того, необходимо изучить дифракцию на пространственной решетке и уметь пользоваться формулой Вульфа — Брэгга, являющейся основной в рентгеноструктурном анализе, имеющем важнейшее практическое применение.
Изучение явлений интерференции и дифракции света должно подготовить студента к пониманию основ волновой (квантовой) механики и физики твердого тела.
Поперечность световых волн была экспериментально установлена при изучении явления поляризации света, которое имеет большое практическое применение. При изучении этого явления особое внимание следует обратить на способы получения поляризованного света и применение законов Брюстера, Малюса, на явление вращения плоскости поляризации в кристаллах и растворах, эффект Керра.
Изучая явление дисперсии света, необходимо уяснить сущность электронной теории этого явления, отличие нормальной дисперсии от аномальной.
Следует представлять, что при движении заряженных частиц в веществе в том случае, когда их скорость движения превышает фазовую скорость световых волн в этой среде, возникает излучение Вавилова — Черенкова, которое нужно рассматривать как классическое явление.
Переход от классической физики и квантовой связан с проблемой теплового излучения и, в частности, с вопросом распределения энергии по частотам в спектре абсолютно черного тела. Изучая тему «Квантовая природа излучения», необходимо знать
гипотезу Планка о квантовании энергии осцилляторов и уяснить, что на основании формулы Планка могут быть получены законы Стефана — Больцмана и Вина.
Развитие гипотезы Планка привело к созданию представлений о квантовых свойствах света. Кванты света получили название фотонов. С позиций квантовой теории света объясняются такие явления, как фотоэлектрический эффект и эффект Комптона. При изучении фотоэффекта следует знать формулу Эйнштейна и на ее основании уметь объяснить закономерности, установленные Столетовым.
Рассматривая эффект Комптона, необходимо обратить внимание на универсальный характер законов сохранения, которые оказываются справедливыми в каждом отдельном акте взаимодействия фотона с электроном.
Изучая световое давление, важно понять, что это явление может быть объяснено как на основе волновых представлений о свете, так и с точки зрения квантовой теории.
В итоге изучения этого раздела у студента должно сформироваться представление, что электромагнитное излучение имеет двойственную корпускулярно-волновую природу (корпускулярно-волновой дуализм). Корпускулярно-волновой дуализм является проявлением взаимосвязи двух основных форм материи: вещества и поля.
Контрольная работа № 3 построена таким образом, что дает возможность проверить знания студентов по разделу «Колебания. Волны. Оптика».
Задачи на гармонические колебания охватывают такие вопросы, как определение амплитуды скорости, ускорения, энергии, периода механических колебаний, силы тока, напряжения, энергии и частоты электромагнитных колебаний.
Волновые процессы представлены задачами, в которых определяются частота, длина, скорость распространения, энергия и объемная плотность энергии механических и электромагнитных волн.
Задачи по теме «Интерференция света» включают расчет интерференционной картины от двух когерентных источников, интерференцию в тонких пленках, полосы равной толщины и равного наклона.
Тема «Дифракция света» представлена задачами: зоны Френеля, дифракция в параллельных лучах на одной щели, на плоской и пространственной дифракционных решетках, разрешающая способность дифракционной решетки.
Задачи по теме «Поляризация света» охватывают такие вопросы, как применение законов Брюстера, Малюса, определение степени поляризации, вращение плоскости поляризации в растворах и кристаллах.
Тема «Распространение света в веществе» включают законы
теплового излучения, фотоэффект, эффект Комптона, давление света.
ОСНОВНЫЕ ФОРМУЛЫ
Уравнение гармонического колебания где А — амплитуда колебания, со — циклическая частота, Фо — начальная фаза.
Период колебания маятников: пружинного физического
где т — масса маятника,
к — жесткость пружины,
J — момент инерции маятника, g — ускорение свободного падения,
I — расстояние от точки подвеса до центра масс.
Период колебании в электрическом колебательном контуре
где L — индуктивность контура, С — емкость конденсатора.
Уравнение плоской волны, распространяющейся в направлении оси Ох, где v — скорость распространения волны.
Длина волны
где Т — период волны.
Скорость распространения электромагнитной волны
где с — скорость света в вакууме, е — диэлектрическая проницаемость среды,
р — магнитная проницаемость.
Скорость распространения звука в газах

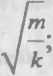
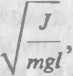

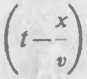
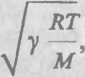





s=A 8ш(оЯ+ф0),
Т=2л
Т=2п
Т=2п у/LC,
5=Л sin
со
+ фо
где у — отношение теплоемкостей газа, при постоянном давлении и объеме,
R — молярная газовая постоянная,
Т — термодинамическая температура,
М — молярная масса газа.
Вектор Пойнтинга
где Е и Н — напряженности электрического и магнитного полей электромагнитной волны.
Оптическая длина пути в однородной среде
где s — геометрическая длина пути световой волны,
п — показатель преломления среды.
Оптическая разность хода
где £i и Ь2 — оптические пути двух световых волн.
Условие интерференционного максимума



р=Е хН,
L=ns,
Д= ±тлЛ), щ=0, 1, 2, ..
и интерференционного минимума Д = ± (2/л — 1 )2о/2, m = 1, 2
где — длина световой волны в вакууме.
Ширина интерференционных полос в опыте Юнга
где d — расстояние между когерентными источниками света,
Z — расстояние от источников до экрана.
Оптическая разность хода в тонких пленках:
в проходящем свете
в отраженном свете
где d — толщина пленки,
п — показатель преломления пленки,
i — угол падения света.


Д=2d у/п2 — sin2 i;
Д = 2d ^/и2 —sin2 i——
2
rm=y/m).R, щ=1, 2, ...
Радиусы светлых колец Ньютона в проходящем свете или темных в отраженном

rw=V(2^-l)lR/2,
w=l, 2,...,
и темных колец в проходящем свете или светлых в отраженном
где А — радиус кривизны линзы,
Л — длина световой волны в среде.
Радиусы зон Френеля

rm=y/m).abl(a+b\
m=l, 2,...;
гт—^т2Ь, w=l, 2,...,
для сферической волновой поверхности
для плоской волновой поверхности
а — радиус волновой поверхности,
b — кратчайшее расстояние от волновой поверхности до точки наблюдения.
Направление дифракционных макси
мумов от одной щели ср0—0, a sin cpm = ± (2т +1 )2/2
т=1, 2, ...;
и дифракционных минимумов a sin фт= +/л2, т= 1, 2, ...,
где а — ширина щели.
Направление главных максимумов
дифракционной решетки csin
m= +m).t m=Q, 1, 2, ...,
где с — постоянная дифракционной решетки.
Разрешающая способность дифракци-
онной решетки R=—=mN,
ДА
где ДА — минимальная разность длин волн двух, спектральных линий, разрешаемых решеткой, т — порядок спектра, N — общее число щелей решетки.
Формула Вульфа — Брэгга 2dsin6т=т2, т= 1, 2, ...,
где d — расстояние между атомными плоскостями кристалла, 6т — угол скольжения рентге
новских лучей. Т j
Степень поляризации
ЛпахAnin

Л2 tg io=-, «1
где Лим и /щщ — максимальная и минимальная интенсивность света.
Закон Брюстера
где io — угол Брюстера,

/=7ocos2 а,
и п2 — показатели преломлений первой и второй среды.
Закон Малюса
где 10 и I — интенсивность плоско- поляризованного света, падающего и прошедшего через поляризатор,
а — угол между плоскостью поляризации падающего света и главной плоскостью поляризатора.
Угол поворота плоскости поляризации света

Ф=Фо/;
ф = [фо]с/,
в кристаллах и чистых жидкостях
в растворах
ср0 — постоянная вращения, [фо] — удельная постоянная враще
ния,
с — концентрация оптически активного вещества в растворе,
/ — расстояние, пройденное светом в оптически активном веществе.
Фазовая скорость света

D=—.
dZ
где с — скорость света в вакууме, п — показатель преломления среды.

Z dn
Дисперсия вещества

п dZ
Групповая скорость света

с
COS0 =—,
nv
Направление излучения Вавилова — Черенкова
где v — скорость заряженной частицы.
Закон Стефана — Больцмана
где А—энергетическая светимость черного тела,
Т— термодинамическая температура тела,
о — постоянная Стефана — Больцмана.
Закон смещения Вина
где Лаи — длина волны, на которую приходится максимум энергии излучения черного тела
b — постоянная Вина.
Давление света при нормальном падении на поверхность
где I — интенсивность света,
р — коэффициент отражения,
и>—объемная плотность энергии излучения.
Энергия фотона
где h — постоянная Планка, v — частота света.
Уравнение Эйнштейна для внешнего фотоэффекта
где А — работа выхода электронов из металла,
Ттах — максимальная кинетическая энергия фотоэлектронов.
Комптоновская длина волны частицы
де т0—масса покоя частицы,
Ео—энергия покоя частицы.
Изменение длины волны рентгеновского излучения при эффекте Комптона
R=aT\
_Ь ia*—
Р=
(l+p)=w(l+p), С
max>
. _ Л _hc'
ПОЯСНЕНИЯ К РАБОЧЕЙ ПРОГРАММЕ
При изучении темы «Колебания» следует параллельно рассматривать механические и электромагнитные колебания, что способствует выработке у студента единого подхода к колебаниям различной физической природы. Здесь следует четко уяснить понятия фазы, разности фаз, амплитуды, частоты, периода колебаний, и там, где это необходимо, использовать графический метод представления гармонического колебания. Нужно уяснить, что любые колебания линейной системы всегда можно представить в виде суперпозиции одновременно совершающихся гармонических колебаний с различными частотами, амплитудами и начальными фазами.
Изучение темы «Волны» целесообразно начинать с механических волн, распространяющихся в упругих средах. Здесь следует обратить внимание на картину мгновенного распределения смещений и скоростей в бегущей волне, различие между бегущей и стоячей волнами, зависимость фазовой скорости от частоты колебаний, найти связь между групповой и фазовой скоростями и показать их равенство в отсутствие дисперсии волн. Особое внимание студент должен уделить условию интерференции волн, энергетическому соотношению при интерференции волн, понять и объяснить перераспределение энергии при образовании минимумов и максимумов интенсивности. Переходя к изучению электромагнитных волн, студенту следует ясно представить себе физический смысл уравнений Максвелла и, опираясь на них, рассмотреть свойства этих волн. Нужно четко представлять, что переменные электрическое и магнитное поля взаимосвязаны, они поддерживают друг друга и могут существовать независимо от источника, их породившего, распространяясь в пространстве в виде электромагнитной волны. Другими словами, электромагнитная волна — это распространяющееся в пространстве переменное электромагнитное поле. Под энергией электромагнитного поля следует подразумевать сумму энергий электрического и магнит- 88
ного полей. Простейшей системой, излучающей электромагнитные волны, является колеблющийся электрический диполь. Следует помнить, что если диполь совершает гармонические колебания, то он излучает монохроматическую волну.
В настоящее время волновая оптика является частью общего учения о распространении волн. При изучении явлений интерференции, дифракции, объясняемых с позиций волновой природы света, студент должен обратить внимание на общность этих явлений для волн любой природы. Но световые волны имеют специфические особенности, когерентность, монохроматичность, которые обусловлены конечной длительностью свечения отдельного атома.
При изучении интерференции света особое внимание следует обратить на такие вопросы, как цвета тонких пленок, полосы равной толщины и равного наклона. Следует помнить, что при интерференции света имеет место суперпозиция, связанная с перераспределением энергии, а не с взаимодействием волн.
Рассматривая явление дифракции, необходимо уяснить метод зон Френеля, уметь пользоваться графическим методом сложения амплитуд, что будет способствовать пониманию дифракции на одной щели, дифракционной решетке. Кроме того, необходимо изучить дифракцию на пространственной решетке и уметь пользоваться формулой Вульфа — Брэгга, являющейся основной в рентгеноструктурном анализе, имеющем важнейшее практическое применение.
Изучение явлений интерференции и дифракции света должно подготовить студента к пониманию основ волновой (квантовой) механики и физики твердого тела.
Поперечность световых волн была экспериментально установлена при изучении явления поляризации света, которое имеет большое практическое применение. При изучении этого явления особое внимание следует обратить на способы получения поляризованного света и применение законов Брюстера, Малюса, на явление вращения плоскости поляризации в кристаллах и растворах, эффект Керра.
Изучая явление дисперсии света, необходимо уяснить сущность электронной теории этого явления, отличие нормальной дисперсии от аномальной.
Следует представлять, что при движении заряженных частиц в веществе в том случае, когда их скорость движения превышает фазовую скорость световых волн в этой среде, возникает излучение Вавилова — Черенкова, которое нужно рассматривать как классическое явление.
Переход от классической физики и квантовой связан с проблемой теплового излучения и, в частности, с вопросом распределения энергии по частотам в спектре абсолютно черного тела. Изучая тему «Квантовая природа излучения», необходимо знать
гипотезу Планка о квантовании энергии осцилляторов и уяснить, что на основании формулы Планка могут быть получены законы Стефана — Больцмана и Вина.
Развитие гипотезы Планка привело к созданию представлений о квантовых свойствах света. Кванты света получили название фотонов. С позиций квантовой теории света объясняются такие явления, как фотоэлектрический эффект и эффект Комптона. При изучении фотоэффекта следует знать формулу Эйнштейна и на ее основании уметь объяснить закономерности, установленные Столетовым.
Рассматривая эффект Комптона, необходимо обратить внимание на универсальный характер законов сохранения, которые оказываются справедливыми в каждом отдельном акте взаимодействия фотона с электроном.
Изучая световое давление, важно понять, что это явление может быть объяснено как на основе волновых представлений о свете, так и с точки зрения квантовой теории.
В итоге изучения этого раздела у студента должно сформироваться представление, что электромагнитное излучение имеет двойственную корпускулярно-волновую природу (корпускулярно-волновой дуализм). Корпускулярно-волновой дуализм является проявлением взаимосвязи двух основных форм материи: вещества и поля.
Контрольная работа № 3 построена таким образом, что дает возможность проверить знания студентов по разделу «Колебания. Волны. Оптика».
Задачи на гармонические колебания охватывают такие вопросы, как определение амплитуды скорости, ускорения, энергии, периода механических колебаний, силы тока, напряжения, энергии и частоты электромагнитных колебаний.
Волновые процессы представлены задачами, в которых определяются частота, длина, скорость распространения, энергия и объемная плотность энергии механических и электромагнитных волн.
Задачи по теме «Интерференция света» включают расчет интерференционной картины от двух когерентных источников, интерференцию в тонких пленках, полосы равной толщины и равного наклона.
Тема «Дифракция света» представлена задачами: зоны Френеля, дифракция в параллельных лучах на одной щели, на плоской и пространственной дифракционных решетках, разрешающая способность дифракционной решетки.
Задачи по теме «Поляризация света» охватывают такие вопросы, как применение законов Брюстера, Малюса, определение степени поляризации, вращение плоскости поляризации в растворах и кристаллах.
Тема «Распространение света в веществе» включают законы
теплового излучения, фотоэффект, эффект Комптона, давление света.
ОСНОВНЫЕ ФОРМУЛЫ
Уравнение гармонического колебания где А — амплитуда колебания, со — циклическая частота, Фо — начальная фаза.
Период колебания маятников: пружинного физического
где т — масса маятника,
к — жесткость пружины,
J — момент инерции маятника, g — ускорение свободного падения,
I — расстояние от точки подвеса до центра масс.
Период колебании в электрическом колебательном контуре
где L — индуктивность контура, С — емкость конденсатора.
Уравнение плоской волны, распространяющейся в направлении оси Ох, где v — скорость распространения волны.
Длина волны
где Т — период волны.
Скорость распространения электромагнитной волны
где с — скорость света в вакууме, е — диэлектрическая проницаемость среды,
р — магнитная проницаемость.
Скорость распространения звука в газах

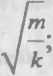
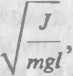

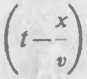
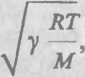





s=A 8ш(оЯ+ф0),
Т=2л
Т=2п
Т=2п у/LC,
5=Л sin
со
+ фо
где у — отношение теплоемкостей газа, при постоянном давлении и объеме,
R — молярная газовая постоянная,
Т — термодинамическая температура,
М — молярная масса газа.
Вектор Пойнтинга
где Е и Н — напряженности электрического и магнитного полей электромагнитной волны.
Оптическая длина пути в однородной среде
где s — геометрическая длина пути световой волны,
п — показатель преломления среды.
Оптическая разность хода
где £i и Ь2 — оптические пути двух световых волн.
Условие интерференционного максимума



р=Е хН,
L=ns,
Д= ±тлЛ), щ=0, 1, 2, ..
и интерференционного минимума Д = ± (2/л — 1 )2о/2, m = 1, 2
где — длина световой волны в вакууме.
Ширина интерференционных полос в опыте Юнга
где d — расстояние между когерентными источниками света,
Z — расстояние от источников до экрана.
Оптическая разность хода в тонких пленках:
в проходящем свете
в отраженном свете
где d — толщина пленки,
п — показатель преломления пленки,
i — угол падения света.


Д=2d у/п2 — sin2 i;
Д = 2d ^/и2 —sin2 i——
2
rm=y/m).R, щ=1, 2, ...
Радиусы светлых колец Ньютона в проходящем свете или темных в отраженном

rw=V(2^-l)lR/2,
w=l, 2,...,
и темных колец в проходящем свете или светлых в отраженном
где А — радиус кривизны линзы,
Л — длина световой волны в среде.
Радиусы зон Френеля

rm=y/m).abl(a+b\
m=l, 2,...;
гт—^т2Ь, w=l, 2,...,
для сферической волновой поверхности
для плоской волновой поверхности
а — радиус волновой поверхности,
b — кратчайшее расстояние от волновой поверхности до точки наблюдения.
Направление дифракционных макси
мумов от одной щели ср0—0, a sin cpm = ± (2т +1 )2/2
т=1, 2, ...;
и дифракционных минимумов a sin фт= +/л2, т= 1, 2, ...,
где а — ширина щели.
Направление главных максимумов
дифракционной решетки csin
m= +m).t m=Q, 1, 2, ...,
где с — постоянная дифракционной решетки.
Разрешающая способность дифракци-
онной решетки R=—=mN,
ДА
где ДА — минимальная разность длин волн двух, спектральных линий, разрешаемых решеткой, т — порядок спектра, N — общее число щелей решетки.
Формула Вульфа — Брэгга 2dsin6т=т2, т= 1, 2, ...,
где d — расстояние между атомными плоскостями кристалла, 6т — угол скольжения рентге
новских лучей. Т j
Степень поляризации
ЛпахAnin

Л2 tg io=-, «1
где Лим и /щщ — максимальная и минимальная интенсивность света.
Закон Брюстера
где io — угол Брюстера,

/=7ocos2 а,
и п2 — показатели преломлений первой и второй среды.
Закон Малюса
где 10 и I — интенсивность плоско- поляризованного света, падающего и прошедшего через поляризатор,
а — угол между плоскостью поляризации падающего света и главной плоскостью поляризатора.
Угол поворота плоскости поляризации света

Ф=Фо/;
ф = [фо]с/,
в кристаллах и чистых жидкостях
в растворах
ср0 — постоянная вращения, [фо] — удельная постоянная враще
ния,
с — концентрация оптически активного вещества в растворе,
/ — расстояние, пройденное светом в оптически активном веществе.
Фазовая скорость света

D=—.
dZ
где с — скорость света в вакууме, п — показатель преломления среды.

Z dn
Дисперсия вещества

п dZ
Групповая скорость света

с
COS0 =—,
nv
Направление излучения Вавилова — Черенкова
где v — скорость заряженной частицы.
Закон Стефана — Больцмана
где А—энергетическая светимость черного тела,
Т— термодинамическая температура тела,
о — постоянная Стефана — Больцмана.
Закон смещения Вина
где Лаи — длина волны, на которую приходится максимум энергии излучения черного тела
b — постоянная Вина.
Давление света при нормальном падении на поверхность
где I — интенсивность света,
р — коэффициент отражения,
и>—объемная плотность энергии излучения.
Энергия фотона
где h — постоянная Планка, v — частота света.
Уравнение Эйнштейна для внешнего фотоэффекта
где А — работа выхода электронов из металла,
Ттах — максимальная кинетическая энергия фотоэлектронов.
Комптоновская длина волны частицы
де т0—масса покоя частицы,
Ео—энергия покоя частицы.
Изменение длины волны рентгеновского излучения при эффекте Комптона
R=aT\
_Ь ia*—
Р=
(l+p)=w(l+p), С
max>
. _ Л _hc'
При изучении темы «Колебания» следует параллельно рассматривать механические и электромагнитные колебания, что способствует выработке у студента единого подхода к колебаниям различной физической природы. Здесь следует четко уяснить понятия фазы, разности фаз, амплитуды, частоты, периода колебаний, и там, где это необходимо, использовать графический метод представления гармонического колебания. Нужно уяснить, что любые колебания линейной системы всегда можно представить в виде суперпозиции одновременно совершающихся гармонических колебаний с различными частотами, амплитудами и начальными фазами.
Изучение темы «Волны» целесообразно начинать с механических волн, распространяющихся в упругих средах. Здесь следует обратить внимание на картину мгновенного распределения смещений и скоростей в бегущей волне, различие между бегущей и стоячей волнами, зависимость фазовой скорости от частоты колебаний, найти связь между групповой и фазовой скоростями и показать их равенство в отсутствие дисперсии волн. Особое внимание студент должен уделить условию интерференции волн, энергетическому соотношению при интерференции волн, понять и объяснить перераспределение энергии при образовании минимумов и максимумов интенсивности. Переходя к изучению электромагнитных волн, студенту следует ясно представить себе физический смысл уравнений Максвелла и, опираясь на них, рассмотреть свойства этих волн. Нужно четко представлять, что переменные электрическое и магнитное поля взаимосвязаны, они поддерживают друг друга и могут существовать независимо от источника, их породившего, распространяясь в пространстве в виде электромагнитной волны. Другими словами, электромагнитная волна — это распространяющееся в пространстве переменное электромагнитное поле. Под энергией электромагнитного поля следует подразумевать сумму энергий электрического и магнит- 88
ного полей. Простейшей системой, излучающей электромагнитные волны, является колеблющийся электрический диполь. Следует помнить, что если диполь совершает гармонические колебания, то он излучает монохроматическую волну.
В настоящее время волновая оптика является частью общего учения о распространении волн. При изучении явлений интерференции, дифракции, объясняемых с позиций волновой природы света, студент должен обратить внимание на общность этих явлений для волн любой природы. Но световые волны имеют специфические особенности, когерентность, монохроматичность, которые обусловлены конечной длительностью свечения отдельного атома.
При изучении интерференции света особое внимание следует обратить на такие вопросы, как цвета тонких пленок, полосы равной толщины и равного наклона. Следует помнить, что при интерференции света имеет место суперпозиция, связанная с перераспределением энергии, а не с взаимодействием волн.
Рассматривая явление дифракции, необходимо уяснить метод зон Френеля, уметь пользоваться графическим методом сложения амплитуд, что будет способствовать пониманию дифракции на одной щели, дифракционной решетке. Кроме того, необходимо изучить дифракцию на пространственной решетке и уметь пользоваться формулой Вульфа — Брэгга, являющейся основной в рентгеноструктурном анализе, имеющем важнейшее практическое применение.
Изучение явлений интерференции и дифракции света должно подготовить студента к пониманию основ волновой (квантовой) механики и физики твердого тела.
Поперечность световых волн была экспериментально установлена при изучении явления поляризации света, которое имеет большое практическое применение. При изучении этого явления особое внимание следует обратить на способы получения поляризованного света и применение законов Брюстера, Малюса, на явление вращения плоскости поляризации в кристаллах и растворах, эффект Керра.
Изучая явление дисперсии света, необходимо уяснить сущность электронной теории этого явления, отличие нормальной дисперсии от аномальной.
Следует представлять, что при движении заряженных частиц в веществе в том случае, когда их скорость движения превышает фазовую скорость световых волн в этой среде, возникает излучение Вавилова — Черенкова, которое нужно рассматривать как классическое явление.
Переход от классической физики и квантовой связан с проблемой теплового излучения и, в частности, с вопросом распределения энергии по частотам в спектре абсолютно черного тела. Изучая тему «Квантовая природа излучения», необходимо знать
гипотезу Планка о квантовании энергии осцилляторов и уяснить, что на основании формулы Планка могут быть получены законы Стефана — Больцмана и Вина.
Развитие гипотезы Планка привело к созданию представлений о квантовых свойствах света. Кванты света получили название фотонов. С позиций квантовой теории света объясняются такие явления, как фотоэлектрический эффект и эффект Комптона. При изучении фотоэффекта следует знать формулу Эйнштейна и на ее основании уметь объяснить закономерности, установленные Столетовым.
Рассматривая эффект Комптона, необходимо обратить внимание на универсальный характер законов сохранения, которые оказываются справедливыми в каждом отдельном акте взаимодействия фотона с электроном.
Изучая световое давление, важно понять, что это явление может быть объяснено как на основе волновых представлений о свете, так и с точки зрения квантовой теории.
В итоге изучения этого раздела у студента должно сформироваться представление, что электромагнитное излучение имеет двойственную корпускулярно-волновую природу (корпускулярно-волновой дуализм). Корпускулярно-волновой дуализм является проявлением взаимосвязи двух основных форм материи: вещества и поля.
Контрольная работа № 3 построена таким образом, что дает возможность проверить знания студентов по разделу «Колебания. Волны. Оптика».
Задачи на гармонические колебания охватывают такие вопросы, как определение амплитуды скорости, ускорения, энергии, периода механических колебаний, силы тока, напряжения, энергии и частоты электромагнитных колебаний.
Волновые процессы представлены задачами, в которых определяются частота, длина, скорость распространения, энергия и объемная плотность энергии механических и электромагнитных волн.
Задачи по теме «Интерференция света» включают расчет интерференционной картины от двух когерентных источников, интерференцию в тонких пленках, полосы равной толщины и равного наклона.
Тема «Дифракция света» представлена задачами: зоны Френеля, дифракция в параллельных лучах на одной щели, на плоской и пространственной дифракционных решетках, разрешающая способность дифракционной решетки.
Задачи по теме «Поляризация света» охватывают такие вопросы, как применение законов Брюстера, Малюса, определение степени поляризации, вращение плоскости поляризации в растворах и кристаллах.
Тема «Распространение света в веществе» включают законы
теплового излучения, фотоэффект, эффект Комптона, давление света.
ОСНОВНЫЕ ФОРМУЛЫ
Уравнение гармонического колебания где А — амплитуда колебания, со — циклическая частота, Фо — начальная фаза.
Период колебания маятников: пружинного физического
где т — масса маятника,
к — жесткость пружины,
J — момент инерции маятника, g — ускорение свободного падения,
I — расстояние от точки подвеса до центра масс.
Период колебании в электрическом колебательном контуре
где L — индуктивность контура, С — емкость конденсатора.
Уравнение плоской волны, распространяющейся в направлении оси Ох, где v — скорость распространения волны.
Длина волны
где Т — период волны.
Скорость распространения электромагнитной волны
где с — скорость света в вакууме, е — диэлектрическая проницаемость среды,
р — магнитная проницаемость.
Скорость распространения звука в газах


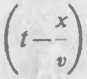





s=A 8ш(оЯ+ф0),
Т=2л
Т=2п
Т=2п у/LC,
5=Л sin
со
+ фо
где у — отношение теплоемкостей газа, при постоянном давлении и объеме,
R — молярная газовая постоянная,
Т — термодинамическая температура,
М — молярная масса газа.
Вектор Пойнтинга
где Е и Н — напряженности электрического и магнитного полей электромагнитной волны.
Оптическая длина пути в однородной среде
где s — геометрическая длина пути световой волны,
п — показатель преломления среды.
Оптическая разность хода
где £i и Ь2 — оптические пути двух световых волн.
Условие интерференционного максимума



р=Е хН,
L=ns,
Д= ±тлЛ), щ=0, 1, 2, ..
и интерференционного минимума Д = ± (2/л — 1 )2о/2, m = 1, 2
где — длина световой волны в вакууме.
Ширина интерференционных полос в опыте Юнга
где d — расстояние между когерентными источниками света,
Z — расстояние от источников до экрана.
Оптическая разность хода в тонких пленках:
в проходящем свете
в отраженном свете
где d — толщина пленки,
п — показатель преломления пленки,
i — угол падения света.


Д=2d у/п2 — sin2 i;
Д = 2d ^/и2 —sin2 i——
2
rm=y/m).R, щ=1, 2, ...
Радиусы светлых колец Ньютона в проходящем свете или темных в отраженном

rw=V(2^-l)lR/2,
w=l, 2,...,
и темных колец в проходящем свете или светлых в отраженном
где А — радиус кривизны линзы,
Л — длина световой волны в среде.
Радиусы зон Френеля

rm=y/m).abl(a+b\
m=l, 2,...;
гт—^т2Ь, w=l, 2,...,
для сферической волновой поверхности
для плоской волновой поверхности
а — радиус волновой поверхности,
b — кратчайшее расстояние от волновой поверхности до точки наблюдения.
Направление дифракционных макси
мумов от одной щели ср0—0, a sin cpm = ± (2т +1 )2/2
т=1, 2, ...;
и дифракционных минимумов a sin фт= +/л2, т= 1, 2, ...,
где а — ширина щели.
Направление главных максимумов
дифракционной решетки csin
m= +m).t m=Q, 1, 2, ...,
где с — постоянная дифракционной решетки.
Разрешающая способность дифракци-
онной решетки R=—=mN,
ДА
где ДА — минимальная разность длин волн двух, спектральных линий, разрешаемых решеткой, т — порядок спектра, N — общее число щелей решетки.
Формула Вульфа — Брэгга 2dsin6т=т2, т= 1, 2, ...,
где d — расстояние между атомными плоскостями кристалла, 6т — угол скольжения рентге
новских лучей. Т j
Степень поляризации
ЛпахAnin

Л2 tg io=-, «1
где Лим и /щщ — максимальная и минимальная интенсивность света.
Закон Брюстера
где io — угол Брюстера,

/=7ocos2 а,
и п2 — показатели преломлений первой и второй среды.
Закон Малюса
где 10 и I — интенсивность плоско- поляризованного света, падающего и прошедшего через поляризатор,
а — угол между плоскостью поляризации падающего света и главной плоскостью поляризатора.
Угол поворота плоскости поляризации света

Ф=Фо/;
ф = [фо]с/,
в кристаллах и чистых жидкостях
в растворах
ср0 — постоянная вращения, [фо] — удельная постоянная враще
ния,
с — концентрация оптически активного вещества в растворе,
/ — расстояние, пройденное светом в оптически активном веществе.
Фазовая скорость света

D=—.
dZ
где с — скорость света в вакууме, п — показатель преломления среды.

Z dn
Дисперсия вещества

п dZ
Групповая скорость света

с
COS0 =—,
nv
Направление излучения Вавилова — Черенкова
где v — скорость заряженной частицы.
Закон Стефана — Больцмана
где А—энергетическая светимость черного тела,
Т— термодинамическая температура тела,
о — постоянная Стефана — Больцмана.
Закон смещения Вина
где Лаи — длина волны, на которую приходится максимум энергии излучения черного тела
b — постоянная Вина.
Давление света при нормальном падении на поверхность
где I — интенсивность света,
р — коэффициент отражения,
и>—объемная плотность энергии излучения.
Энергия фотона
где h — постоянная Планка, v — частота света.
Уравнение Эйнштейна для внешнего фотоэффекта
где А — работа выхода электронов из металла,
Ттах — максимальная кинетическая энергия фотоэлектронов.
Комптоновская длина волны частицы
де т0—масса покоя частицы,
Ео—энергия покоя частицы.
Изменение длины волны рентгеновского излучения при эффекте Комптона
R=aT\
_Ь ia*—
Р=
тос Ео
A;.=Z-2=2c(l-cos0)=
= 22csin2(0/2),
где 2 и Л'—длина волны падающего и рассеянного излучения, В — угол рассеяния.