Файл: Методические указания и контрольные задания для студентовзаочников инженернотехнических и технологических специальностей вузов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 252
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
E=Ej Ч-Ез.
По теореме косинусов
Е=у/Ё11+ё(+2Ё1 ' £? • cos 2а. (2)
Напряженность поля точечного заряда Q
E=QI(4nEE0r2)f
где е — диэлектрическая проницаемость; Ео — электрическая постоянная; г — расстояние от заряда до точки поля, в которой определяется его напряженность. Заряды 61 и Ол отрицательны, следовательно, векторы его Ет и Е2 направлены по линиям напряженности к зарядам. По условию заряды Q\ — Q2 расположены на одинаковом расстоянии от точки Л, поэтому ЕХ=Е2. Следовательно, формула (2) принимает вид Е=2ЕХ • cos а, где cosa—h/r^
h=OA=^rl-rll4;
h=-J(5 ■ 10'2 м2)2—(4 ' IO"2 м)2 = 3 • 10'2 м.
Тогда напряженность в точке А
2Qi h
^=—
47Г££оГ^

=480 В/м.
2 9 1(Г9 Кл 3 10"2 м
4 3,14 81 8,85 10"12 Ф/м (0,05)3 м2
Потенциал ф, создаваемый системой точечных зарядов в данной точке поля, равен алгебраической сумме потенциалов, создава-
емых каждым из зарядов ср = £ (р±. Потенциал ср результирующе- 1"1 т-г
го поля в точке А равен (p = cpi + cp2- Потенциал поля, создава
емого точечным зарядом, ф=(2/(47гее0г). Следовательно,
Ci 0.2 201
= ,+ <р2=- ;
47Г££ог1 4Я££оГ2 4Я££оГ1
4 3,14 81 8,85 10’12 Ф/м 5 10'2
Ответ’. £=480 В/м; (р — — 40 В.
-
Заряд 1 нКл переносится в воздухе из точки, находящейся на расстоянии 1 м от бесконечно длинной равномерно заряженной нити, в точку на расстоянии 10 см от нее. Определить работу, совершаемую против сил поля, если линейная плотность заряда нити 1 мкКл/м. Какая работа совершается на последних 10 см пути?
Дано: го=О,1 м; п = 1 м; г2=0,2 м; Q=1 109 Кл; е=1; т= 1 • 10-6 Кл/м.
Найти: А2.
Решение. Работа внешней силы по перемещению заряда Q из точки поля с потенциалом (pt в точку с потенциалом <р0 равна
^ = С(фоФ1). О)
Бесконечная равномерно заряженная нить с линейной плотностью заряда т создает аксиально-симметричное поле напряженностью £=т/(27гее0г). Напряженность и потенциал этого поля d
связаны соотношением £= , откуда d
Edr. Разность
dr
потенциалов точек поля на расстоянии г, и г0 от нити
Г0


Фо-ф.= -
£dr =
т f dr т г*
-= In
2леео J г 2пеео го
г

И In
Го
i
Т
Фо-<Р1 = П
2Л6£о

(2)
Г2
(Р0-(Р2 = — Ь
2я££0 г0
Подставляя в формулу (1) найденное выражение для разности потенциалов из (2), определим работу, совершаемую внешними силами по перемещению заряда из точки, находящейся на расстоянии 1 м, до точки, расположенной на расстоянии 0,1 м от нити:
2л££о го’

• 10'J Дж.
, 1 • 10’9 Кл 1 • 1О’€ Кл/м In 10 , .
А1 = — =4,1
2 3,14 8,85 1012 Ф/м
„ 1 • 10"9 ■ 1 • 10€ In 10
Вычислим на калькуляторе выражение —■ по
2 3,14 8,85 10-12
программе
1[вп|9[7ч1И 1®б[Н10 югаа 2 0EI008,85R 1|вп] 12I/-/IR
Показания индикатора: 4,14087 10 5, т. е. 4,1 • 10“5 Дж.
Работа по перемещению заряда на последних 10 см пути равна
С т, Г2
Л2= In -;
2леео г0
, 1 • Ю 9 Кл 10 б Кл/м 1п2 , _ _ , „
Л2 = 7 - = 1,25 • 10'5 Дж.
2 3,14 8,85 10-12 Ф/м
Ответ: Л1 = 4,1 ' 10 5 Дж; Л2=1,25 • 10 5 Дж.
-
К одной из обкладок плоского конденсатора прилегает стеклянная плоскопараллельная пластинка (£1 = 7) толщиной 9 мм. После того как конденсатор отключили от источника напряжения 220 В и вынули стеклянную пластинку, между обкладками установилась разность потенциалов 976 В. Определить зазор между обкладками и отношение конечной и начальной энергии конденсатора.
Дано: С7!=220 В; (72=976 В; dj = 9 103 м; £1 = 7; е2=1.
Найти: do; W\/W2.
Решение. После отключения конденсатора и удаления стеклянной пластинки заряд на его обкладках остается неизменным, т. е. выполняется равенство
Cit7i = C2t/2, (1)
где С\ и С2 — электроемкости конденсатора в начальном и конечном случае.
По условию конденсатор вначале является слоистым и его электроемкость определяется по формуле
Eg ‘ S

(2)
G= —
di dodi
— +
£1 Е2
где 5 — площадь обкладок; d0 — зазор между ними, dx — толщина стеклянной пластинки, Ej и е2 — диэлектрические проницаемости стекла и воздуха соответственно.

E2£oS
После удаления стеклянной пластинки электроемкость конденсатора
(3)
Подставляя (2) и (3) в (1), получим
£о5С/1 £2£o5L/2
d\ do d\ dQ
£1 £2
откуда

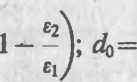






“о—
U2-Ui
976 В 9 IO-3
(976 - 220) В
м
1-’|=1 • 10’2 7/
M.
Начальная и конечная энергии конденсатора
CiU2. C2u22
W\=—; W2=—.
2 2
Тогда отношение этих энергий W2/Wi = C2U2/(CiUl). Учитывая (1), получим
W2 U2 W2 976 В . . .
——• — = 4 44
Wi Uif Wi 220 В
Ответ: do=l ' Ю“2 м; FF2/FFi=4,44.
-
Батарею из двух конденсаторов емкостью 400 и 500 пФ соединили последовательно и включили в сеть с напряжением 220 В. Потом батарею отключили от сети, конденсаторы разъединили и соединили параллельно обкладками, имеющими одноименные заряды. Каким будет напряжение на зажимах полученной батареи?
Дано: £7j = 220 В; Cj=400 пФ; С2=500 пФ.
Найти: U2.
Решение. У последовательно соединенных конденсаторов заряды на обкладках равны по модулю 61 = 62=6 и заряд батареи равен заряду одного конденсатора. Емкость батареи последовательно соединенных конденсаторов определяется по формуле п
1/С= £ 1/С«. Для батареи из двух конденсаторов
С=С, • С2/(С, + С2),
а их заряд
6 = СС/1 = С1С2С/1/(С1 + С2). (1)
При отключении конденсаторов их заряд сохраняется. У параллельно соединенных конденсаторов заряд батареи равен сумме зарядов конденсаторов 6=61 + 62» а емкость — сумме емкостей
С' = С\ + С2.
Напряжение на зажимах батареи из двух параллельно соединенных конденсаторов
Г 7 — R — _ 3^ /п\
2CCl + C2Cl-hC2' '
Подставляя (1) в (2), получаем
2CjC2?7i
(^1 + С2)
гт 2 4 5 • Ю-20 Ф2 • 220 В
tf2 = — - =108,6 В.
92 1О20 Ф2
Ответ'. t/2= 108,6 В.
-
Заряд конденсатора 1 мкКл, площадь пластин 100 см2, зазор между пластинками заполнен слюдой. Определить объемную плотность энергии поля конденсатора и силу притяжения пластин.
Дано: 6=Ю 6 Кл; 5= 10“2 м2; е=6.
Найти: >v; F.

(1)
Решение. Сила притяжения между двумя разноименно заряженными обкладками конденсатора уг .“о£2 5 ” 2
где Е — напряженность поля конденсатора; S — площадь обкладок конденсатора; е — диэлектрическая проницаемость слюды; Eq — электрическая постоянная.

(2)
Напряженность однородного поля плоского конденсатора _ ff Q Е==. ££q EEqS
где o=QIS — поверхностная плотность заряда. Подставляя (2) в (1), получаем
о2 Ю“12 Кл2
— = 0,94 Н. 2&£qS 2 6 8,85 10“12 Ф/м 10“2 м2
Объемная плотность энергии электрического поля

(3)
££qE2
W= — .
2
Подставляя (2) в (3), получаем
Q2 ю12 Кл2 -
w=——w=- —- = 94,2 Дж/м3.
2££0S2 2 • 6 8,85 10“12 Ф/м 10“* м4
Ответ: J’=0,94 Н; w=94,2 Дж/м.
-
В медном проводнике сечением 6 мм и длиной 5 м течет ток. За 1 мин в проводнике выделяется 18 Дж теплоты. Определить напряженность поля, плотность и силу электрического тока в проводнике.
Дано: 5=6 • 106 м2; 1=5 м; /=60 с; Q= 18 Дж; р = 1,7 • 10 8 Ом ■ м.
Найти: £; j; J.
Решение. Для решения задачи используем законы Ома и Джоуля — Ленца. Закон Ома в дифференциальной форме имеет вид
(о где j — плотность тока; Е — напряженность доля; у — удельная проводимость.
Закон Джоуля — Ленца
Q^Rt. (2)
Здесь J — сила тока, t — время,
R=p' (3)
д
— сопротивление проводника, где р, I, S — удельное сопротивление, длина и площадь поперечного сечения проводника соответственно.
Силу тока J находим из (2) с учетом (3):
т [q [qS I 18 Дж 6 10-6 м2
J= /—= / ; 7= -=4,6 A.
у Rt у pit у 1,7 10 8 Ом м 5 м 60 с
По определению, плотность тока равна j=J[S\
j=4,6 А/(6 • 10"6 м2) = 7,7 • 105 А/м2.
Напряженность поля в проводнике определим из (1), учитывая, что у=\1р.
E=j- р; Е=7,7 • 105 А/м2 • 1,7 КГ8 Ом • м=1,3 • 10'2 В/м.
Ответ: Е=1,3 10“2 В/м; J=4,6 A; 7=7,7 ■ 105 А/м2.
-
Внутреннее сопротивление аккумулятора 2 Ом. При замыкании его одним резистором сила тока равна 4 А, при замыкании другим — 2 А. Во внешней цепи в обоих случаях выделяется одинаковая мощность. Определить электродвижущую силу аккумулятора и внешние сопротивления.
Дано: г-2 Ом; 7] = 4 A; J2—2 A; NX=N2.
Найти: <5 ; 2^; R2-
Решение. Закон Ома для замкнутой (полной) цепи имеет вид

где г — внутреннее сопротивление источника тока; & — э. д. с. аккумулятора; R}iiR2 — внешние сопротивления цепей.
Уравнения (1) представим в виде
<5=Л(А, + г); 6=Л№+г). (2)
Из равенства> (2) следует, что
71(А1+г)=Л№+г). (3)
Мощность, выделяемая во внешней цепи в первом и втором случаях, соответственно равна
N2=JiR2.
Из условия равенства мощностей следует, что

Решая совместно уравнения (3) и (4), получаем

(4)
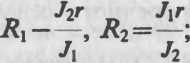

(5)
Л 2 А 2 Ом , _ Л 4 А • 2 Ом л _
— = 1 Ом, R2= = 4 Ом.
4 А 2 А
Подставляя (5) в (2), получаем
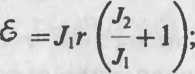 5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
Ответ: & = 12 В; Rt= 1 Ом; Л2 = 4 Ом.
-
Электродвижущая сила батареи равна 20 В. Коэффициент полезного действия батареи составляет 0,8 при силе тока 4 А. Чему равно внутреннее сопротивление батареи?
Дано: £ =20 В; >7 = 0,8; .7=4 А.
Найти: г.
Решение. Коэффициент полезного действия источника тока t] равен отношению падения напряжения во внешней цепи к его электродвижущей силе.
откуда
(2)
Используя выражение закона Ома для замкнутой цепи J= £/(Л+г), получаем
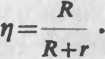
Подставляя (2) в (3) и выполняя преобразования, находим
ё(1-п) 20 в (1-0,8)
г= : г= =1 Ом.
Ответ: г— 1 Ом.
-
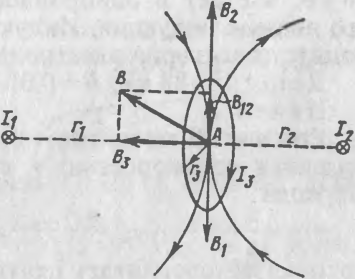
По двум бесконечно длинным прямолинейным проводникам, находящимся на расстоянии 50 см друг от друга, в одном направлении текут токи J\ и J2 силой по 5 А. Между проводниками на расстоянии 30 см от первого расположен кольцевой проводник с током J3 силой 5 А (рис. 3). Радиус кольца 20 см. Определить индукцию и напряженность магнитного поля, создаваемого токами в центре кольцевого проводника.
Дано: J1=J2=J3=J=5 А; ^=0,2 м; г3=0,2 м.
Найти: В\ Н.
Решение. В соответствии с принципом суперпозиции индукция результирующего магнитного поля в точке А равна
В = Bj 4-Вг + В3, (1)
где Bi и В2 — индукции полей, создаваемых соответственно токами Ji и J2, направленными за плоскость рисунка; Вз — индукция поля, создаваемая кольцевым током. Как видно из рис. 3, векторы В) и Bi направлены по одной прямой в противоположные стороны, поэтому их сумма В, 4-82 = 812 равна по модулю
В{2—В2 — Bi. (2)

(3)
Индукция поля, создаваемого бесконечно длинным проводником с током,

где До — магнитная постоянная; д — магнитная проницаемость
о\——; В2———,
2nr\ 2itr2
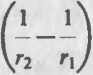




п л12=——
2л
5>
1 ... 4 5 6 7 8 9 10 11 12
E=Ej Ч-Ез.
По теореме косинусов
Е=у/Ё11+ё(+2Ё1 ' £? • cos 2а. (2)
Напряженность поля точечного заряда Q
E=QI(4nEE0r2)f
где е — диэлектрическая проницаемость; Ео — электрическая постоянная; г — расстояние от заряда до точки поля, в которой определяется его напряженность. Заряды 61 и Ол отрицательны, следовательно, векторы его Ет и Е2 направлены по линиям напряженности к зарядам. По условию заряды Q\ — Q2 расположены на одинаковом расстоянии от точки Л, поэтому ЕХ=Е2. Следовательно, формула (2) принимает вид Е=2ЕХ • cos а, где cosa—h/r^
h=OA=^rl-rll4;
h=-J(5 ■ 10'2 м2)2—(4 ' IO"2 м)2 = 3 • 10'2 м.
Тогда напряженность в точке А
2Qi h
^=—
47Г££оГ^

=480 В/м.
2 9 1(Г9 Кл 3 10"2 м
4 3,14 81 8,85 10"12 Ф/м (0,05)3 м2
Потенциал ф, создаваемый системой точечных зарядов в данной точке поля, равен алгебраической сумме потенциалов, создава-
емых каждым из зарядов ср = £ (р±. Потенциал ср результирующе- 1"1 т-г
го поля в точке А равен (p = cpi + cp2- Потенциал поля, создава
емого точечным зарядом, ф=(2/(47гее0г). Следовательно,
Ci 0.2 201
= ,+ <р2=- ;
47Г££ог1 4Я££оГ2 4Я££оГ1
4 3,14 81 8,85 10’12 Ф/м 5 10'2
Ответ’. £=480 В/м; (р — — 40 В.
-
Заряд 1 нКл переносится в воздухе из точки, находящейся на расстоянии 1 м от бесконечно длинной равномерно заряженной нити, в точку на расстоянии 10 см от нее. Определить работу, совершаемую против сил поля, если линейная плотность заряда нити 1 мкКл/м. Какая работа совершается на последних 10 см пути?
Дано: го=О,1 м; п = 1 м; г2=0,2 м; Q=1 109 Кл; е=1; т= 1 • 10-6 Кл/м.
Найти: А2.
Решение. Работа внешней силы по перемещению заряда Q из точки поля с потенциалом (pt в точку с потенциалом <р0 равна
^ = С(фоФ1). О)
Бесконечная равномерно заряженная нить с линейной плотностью заряда т создает аксиально-симметричное поле напряженностью £=т/(27гее0г). Напряженность и потенциал этого поля d
связаны соотношением £= , откуда d
Edr. Разность
dr
потенциалов точек поля на расстоянии г, и г0 от нити
Г0


Фо-ф.= -
£dr =
т f dr т г*
-= In
2леео J г 2пеео го
г

И In
Го
i
Т
Фо-<Р1 = П
2Л6£о

(2)
Г2
(Р0-(Р2 = — Ь
2я££0 г0
Подставляя в формулу (1) найденное выражение для разности потенциалов из (2), определим работу, совершаемую внешними силами по перемещению заряда из точки, находящейся на расстоянии 1 м, до точки, расположенной на расстоянии 0,1 м от нити:
2л££о го’

• 10'J Дж.
, 1 • 10’9 Кл 1 • 1О’€ Кл/м In 10 , .
А1 = — =4,1
2 3,14 8,85 1012 Ф/м
„ 1 • 10"9 ■ 1 • 10€ In 10
Вычислим на калькуляторе выражение —■ по
2 3,14 8,85 10-12
программе
1[вп|9[7ч1И 1®б[Н10 югаа 2 0EI008,85R 1|вп] 12I/-/IR
Показания индикатора: 4,14087 10 5, т. е. 4,1 • 10“5 Дж.
Работа по перемещению заряда на последних 10 см пути равна
С т, Г2
Л2= In -;
2леео г0
, 1 • Ю 9 Кл 10 б Кл/м 1п2 , _ _ , „
Л2 = 7 - = 1,25 • 10'5 Дж.
2 3,14 8,85 10-12 Ф/м
Ответ: Л1 = 4,1 ' 10 5 Дж; Л2=1,25 • 10 5 Дж.
-
К одной из обкладок плоского конденсатора прилегает стеклянная плоскопараллельная пластинка (£1 = 7) толщиной 9 мм. После того как конденсатор отключили от источника напряжения 220 В и вынули стеклянную пластинку, между обкладками установилась разность потенциалов 976 В. Определить зазор между обкладками и отношение конечной и начальной энергии конденсатора.
Дано: С7!=220 В; (72=976 В; dj = 9 103 м; £1 = 7; е2=1.
Найти: do; W\/W2.
Решение. После отключения конденсатора и удаления стеклянной пластинки заряд на его обкладках остается неизменным, т. е. выполняется равенство
Cit7i = C2t/2, (1)
где С\ и С2 — электроемкости конденсатора в начальном и конечном случае.
По условию конденсатор вначале является слоистым и его электроемкость определяется по формуле
Eg ‘ S

(2)
G= —
di dodi
— +
£1 Е2
где 5 — площадь обкладок; d0 — зазор между ними, dx — толщина стеклянной пластинки, Ej и е2 — диэлектрические проницаемости стекла и воздуха соответственно.

E2£oS
После удаления стеклянной пластинки электроемкость конденсатора
(3)
Подставляя (2) и (3) в (1), получим
£о5С/1 £2£o5L/2
d\ do d\ dQ
£1 £2
откуда

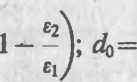






“о—
U2-Ui
976 В 9 IO-3
(976 - 220) В
м
1-’|=1 • 10’2 7/
M.
Начальная и конечная энергии конденсатора
CiU2. C2u22
W\=—; W2=—.
2 2
Тогда отношение этих энергий W2/Wi = C2U2/(CiUl). Учитывая (1), получим
W2 U2 W2 976 В . . .
——• — = 4 44
Wi Uif Wi 220 В
Ответ: do=l ' Ю“2 м; FF2/FFi=4,44.
-
Батарею из двух конденсаторов емкостью 400 и 500 пФ соединили последовательно и включили в сеть с напряжением 220 В. Потом батарею отключили от сети, конденсаторы разъединили и соединили параллельно обкладками, имеющими одноименные заряды. Каким будет напряжение на зажимах полученной батареи?
Дано: £7j = 220 В; Cj=400 пФ; С2=500 пФ.
Найти: U2.
Решение. У последовательно соединенных конденсаторов заряды на обкладках равны по модулю 61 = 62=6 и заряд батареи равен заряду одного конденсатора. Емкость батареи последовательно соединенных конденсаторов определяется по формуле п
1/С= £ 1/С«. Для батареи из двух конденсаторов
С=С, • С2/(С, + С2),
а их заряд
6 = СС/1 = С1С2С/1/(С1 + С2). (1)
При отключении конденсаторов их заряд сохраняется. У параллельно соединенных конденсаторов заряд батареи равен сумме зарядов конденсаторов 6=61 + 62» а емкость — сумме емкостей
С' = С\ + С2.
Напряжение на зажимах батареи из двух параллельно соединенных конденсаторов
Г 7 — R — _ 3^ /п\
2CCl + C2Cl-hC2' '
Подставляя (1) в (2), получаем
2CjC2?7i
(^1 + С2)
гт 2 4 5 • Ю-20 Ф2 • 220 В
tf2 = — - =108,6 В.
92 1О20 Ф2
Ответ'. t/2= 108,6 В.
-
Заряд конденсатора 1 мкКл, площадь пластин 100 см2, зазор между пластинками заполнен слюдой. Определить объемную плотность энергии поля конденсатора и силу притяжения пластин.
Дано: 6=Ю 6 Кл; 5= 10“2 м2; е=6.
Найти: >v; F.

(1)
Решение. Сила притяжения между двумя разноименно заряженными обкладками конденсатора уг .“о£2 5 ” 2
где Е — напряженность поля конденсатора; S — площадь обкладок конденсатора; е — диэлектрическая проницаемость слюды; Eq — электрическая постоянная.

(2)
Напряженность однородного поля плоского конденсатора _ ff Q Е==. ££q EEqS
где o=QIS — поверхностная плотность заряда. Подставляя (2) в (1), получаем
о2 Ю“12 Кл2
— = 0,94 Н. 2&£qS 2 6 8,85 10“12 Ф/м 10“2 м2
Объемная плотность энергии электрического поля

(3)
££qE2
W= — .
2
Подставляя (2) в (3), получаем
Q2 ю12 Кл2 -
w=——w=- —- = 94,2 Дж/м3.
2££0S2 2 • 6 8,85 10“12 Ф/м 10“* м4
Ответ: J’=0,94 Н; w=94,2 Дж/м.
-
В медном проводнике сечением 6 мм и длиной 5 м течет ток. За 1 мин в проводнике выделяется 18 Дж теплоты. Определить напряженность поля, плотность и силу электрического тока в проводнике.
Дано: 5=6 • 106 м2; 1=5 м; /=60 с; Q= 18 Дж; р = 1,7 • 10 8 Ом ■ м.
Найти: £; j; J.
Решение. Для решения задачи используем законы Ома и Джоуля — Ленца. Закон Ома в дифференциальной форме имеет вид
(о где j — плотность тока; Е — напряженность доля; у — удельная проводимость.
Закон Джоуля — Ленца
Q^Rt. (2)
Здесь J — сила тока, t — время,
R=p' (3)
д
— сопротивление проводника, где р, I, S — удельное сопротивление, длина и площадь поперечного сечения проводника соответственно.
Силу тока J находим из (2) с учетом (3):
т [q [qS I 18 Дж 6 10-6 м2
J= /—= / ; 7= -=4,6 A.
у Rt у pit у 1,7 10 8 Ом м 5 м 60 с
По определению, плотность тока равна j=J[S\
j=4,6 А/(6 • 10"6 м2) = 7,7 • 105 А/м2.
Напряженность поля в проводнике определим из (1), учитывая, что у=\1р.
E=j- р; Е=7,7 • 105 А/м2 • 1,7 КГ8 Ом • м=1,3 • 10'2 В/м.
Ответ: Е=1,3 10“2 В/м; J=4,6 A; 7=7,7 ■ 105 А/м2.
-
Внутреннее сопротивление аккумулятора 2 Ом. При замыкании его одним резистором сила тока равна 4 А, при замыкании другим — 2 А. Во внешней цепи в обоих случаях выделяется одинаковая мощность. Определить электродвижущую силу аккумулятора и внешние сопротивления.
Дано: г-2 Ом; 7] = 4 A; J2—2 A; NX=N2.
Найти: <5 ; 2^; R2-
Решение. Закон Ома для замкнутой (полной) цепи имеет вид

где г — внутреннее сопротивление источника тока; & — э. д. с. аккумулятора; R}iiR2 — внешние сопротивления цепей.
Уравнения (1) представим в виде
<5=Л(А, + г); 6=Л№+г). (2)
Из равенства> (2) следует, что
71(А1+г)=Л№+г). (3)
Мощность, выделяемая во внешней цепи в первом и втором случаях, соответственно равна
N2=JiR2.
Из условия равенства мощностей следует, что

Решая совместно уравнения (3) и (4), получаем

(4)
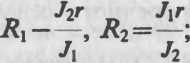

(5)
Л 2 А 2 Ом , _ Л 4 А • 2 Ом л _
— = 1 Ом, R2= = 4 Ом.
4 А 2 А
Подставляя (5) в (2), получаем
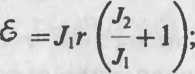 5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
Ответ: & = 12 В; Rt= 1 Ом; Л2 = 4 Ом.
-
Электродвижущая сила батареи равна 20 В. Коэффициент полезного действия батареи составляет 0,8 при силе тока 4 А. Чему равно внутреннее сопротивление батареи?
Дано: £ =20 В; >7 = 0,8; .7=4 А.
Найти: г.
Решение. Коэффициент полезного действия источника тока t] равен отношению падения напряжения во внешней цепи к его электродвижущей силе.
откуда
(2)
Используя выражение закона Ома для замкнутой цепи J= £/(Л+г), получаем
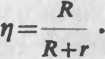
Подставляя (2) в (3) и выполняя преобразования, находим
ё(1-п) 20 в (1-0,8)
г= : г= =1 Ом.
Ответ: г— 1 Ом.
-
По двум бесконечно длинным прямолинейным проводникам, находящимся на расстоянии 50 см друг от друга, в одном направлении текут токи J\ и J2 силой по 5 А. Между проводниками на расстоянии 30 см от первого расположен кольцевой проводник с током J3 силой 5 А (рис. 3). Радиус кольца 20 см. Определить индукцию и напряженность магнитного поля, создаваемого токами в центре кольцевого проводника.
Дано: J1=J2=J3=J=5 А; ^=0,2 м; г3=0,2 м.
Найти: В\ Н.
Решение. В соответствии с принципом суперпозиции индукция результирующего магнитного поля в точке А равна
В = Bj 4-Вг + В3, (1)
где Bi и В2 — индукции полей, создаваемых соответственно токами Ji и J2, направленными за плоскость рисунка; Вз — индукция поля, создаваемая кольцевым током. Как видно из рис. 3, векторы В) и Bi направлены по одной прямой в противоположные стороны, поэтому их сумма В, 4-82 = 812 равна по модулю
В{2—В2 — Bi. (2)

(3)
Индукция поля, создаваемого бесконечно длинным проводником с током,

где До — магнитная постоянная; д — магнитная проницаемость
о\——; В2———,
2nr\ 2itr2
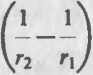





п л12=——
2л
5>
1 ... 4 5 6 7 8 9 10 11 12
E=Ej Ч-Ез.
По теореме косинусов
Е=у/Ё11+ё(+2Ё1 ' £? • cos 2а. (2)
Напряженность поля точечного заряда Q
E=QI(4nEE0r2)f
где е — диэлектрическая проницаемость; Ео — электрическая постоянная; г — расстояние от заряда до точки поля, в которой определяется его напряженность. Заряды 61 и Ол отрицательны, следовательно, векторы его Ет и Е2 направлены по линиям напряженности к зарядам. По условию заряды Q\ — Q2 расположены на одинаковом расстоянии от точки Л, поэтому ЕХ=Е2. Следовательно, формула (2) принимает вид Е=2ЕХ • cos а, где cosa—h/r^
h=OA=^rl-rll4;
h=-J(5 ■ 10'2 м2)2—(4 ' IO"2 м)2 = 3 • 10'2 м.
Тогда напряженность в точке А
2Qi h
^=—
47Г££оГ^

=480 В/м.
2 9 1(Г9 Кл 3 10"2 м
4 3,14 81 8,85 10"12 Ф/м (0,05)3 м2
Потенциал ф, создаваемый системой точечных зарядов в данной точке поля, равен алгебраической сумме потенциалов, создава-
емых каждым из зарядов ср = £ (р±. Потенциал ср результирующе- 1"1 т-г
го поля в точке А равен (p = cpi + cp2- Потенциал поля, создава
емого точечным зарядом, ф=(2/(47гее0г). Следовательно,
Ci 0.2 201
= ,+ <р2=- ;
47Г££ог1 4Я££оГ2 4Я££оГ1
4 3,14 81 8,85 10’12 Ф/м 5 10'2
Ответ’. £=480 В/м; (р — — 40 В.
-
Заряд 1 нКл переносится в воздухе из точки, находящейся на расстоянии 1 м от бесконечно длинной равномерно заряженной нити, в точку на расстоянии 10 см от нее. Определить работу, совершаемую против сил поля, если линейная плотность заряда нити 1 мкКл/м. Какая работа совершается на последних 10 см пути?
Дано: го=О,1 м; п = 1 м; г2=0,2 м; Q=1 109 Кл; е=1; т= 1 • 10-6 Кл/м.
Найти: А2.
Решение. Работа внешней силы по перемещению заряда Q из точки поля с потенциалом (pt в точку с потенциалом <р0 равна
^ = С(фоФ1). О)
Бесконечная равномерно заряженная нить с линейной плотностью заряда т создает аксиально-симметричное поле напряженностью £=т/(27гее0г). Напряженность и потенциал этого поля d
связаны соотношением £= , откуда d
Edr. Разность
dr
потенциалов точек поля на расстоянии г, и г0 от нити
Г0


Фо-ф.= -
£dr =
т f dr т г*
-= In
2леео J г 2пеео го
г

И In
Го
i
Т
Фо-<Р1 = П
2Л6£о

(2)
Г2
(Р0-(Р2 = — Ь
2я££0 г0
Подставляя в формулу (1) найденное выражение для разности потенциалов из (2), определим работу, совершаемую внешними силами по перемещению заряда из точки, находящейся на расстоянии 1 м, до точки, расположенной на расстоянии 0,1 м от нити:
2л££о го’

• 10'J Дж.
, 1 • 10’9 Кл 1 • 1О’€ Кл/м In 10 , .
А1 = — =4,1
2 3,14 8,85 1012 Ф/м
„ 1 • 10"9 ■ 1 • 10€ In 10
Вычислим на калькуляторе выражение —■ по
2 3,14 8,85 10-12
программе
1[вп|9[7ч1И 1®б[Н10 югаа 2 0EI008,85R 1|вп] 12I/-/IR
Показания индикатора: 4,14087 10 5, т. е. 4,1 • 10“5 Дж.
Работа по перемещению заряда на последних 10 см пути равна
С т, Г2
Л2= In -;
2леео г0
, 1 • Ю 9 Кл 10 б Кл/м 1п2 , _ _ , „
Л2 = 7 - = 1,25 • 10'5 Дж.
2 3,14 8,85 10-12 Ф/м
Ответ: Л1 = 4,1 ' 10 5 Дж; Л2=1,25 • 10 5 Дж.
-
К одной из обкладок плоского конденсатора прилегает стеклянная плоскопараллельная пластинка (£1 = 7) толщиной 9 мм. После того как конденсатор отключили от источника напряжения 220 В и вынули стеклянную пластинку, между обкладками установилась разность потенциалов 976 В. Определить зазор между обкладками и отношение конечной и начальной энергии конденсатора.
Дано: С7!=220 В; (72=976 В; dj = 9 103 м; £1 = 7; е2=1.
Найти: do; W\/W2.
Решение. После отключения конденсатора и удаления стеклянной пластинки заряд на его обкладках остается неизменным, т. е. выполняется равенство
Cit7i = C2t/2, (1)
где С\ и С2 — электроемкости конденсатора в начальном и конечном случае.
По условию конденсатор вначале является слоистым и его электроемкость определяется по формуле
Eg ‘ S

(2)
G= —
di dodi
— +
£1 Е2
где 5 — площадь обкладок; d0 — зазор между ними, dx — толщина стеклянной пластинки, Ej и е2 — диэлектрические проницаемости стекла и воздуха соответственно.

E2£oS
После удаления стеклянной пластинки электроемкость конденсатора
(3)
Подставляя (2) и (3) в (1), получим
£о5С/1 £2£o5L/2
d\ do d\ dQ
£1 £2
откуда

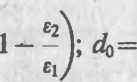






“о—
U2-Ui
976 В 9 IO-3
(976 - 220) В
м
1-’|=1 • 10’2 7/
M.
Начальная и конечная энергии конденсатора
CiU2. C2u22
W\=—; W2=—.
2 2
Тогда отношение этих энергий W2/Wi = C2U2/(CiUl). Учитывая (1), получим
W2 U2 W2 976 В . . .
——• — = 4 44
Wi Uif Wi 220 В
Ответ: do=l ' Ю“2 м; FF2/FFi=4,44.
-
Батарею из двух конденсаторов емкостью 400 и 500 пФ соединили последовательно и включили в сеть с напряжением 220 В. Потом батарею отключили от сети, конденсаторы разъединили и соединили параллельно обкладками, имеющими одноименные заряды. Каким будет напряжение на зажимах полученной батареи?
Дано: £7j = 220 В; Cj=400 пФ; С2=500 пФ.
Найти: U2.
Решение. У последовательно соединенных конденсаторов заряды на обкладках равны по модулю 61 = 62=6 и заряд батареи равен заряду одного конденсатора. Емкость батареи последовательно соединенных конденсаторов определяется по формуле п
1/С= £ 1/С«. Для батареи из двух конденсаторов
С=С, • С2/(С, + С2),
а их заряд
6 = СС/1 = С1С2С/1/(С1 + С2). (1)
При отключении конденсаторов их заряд сохраняется. У параллельно соединенных конденсаторов заряд батареи равен сумме зарядов конденсаторов 6=61 + 62» а емкость — сумме емкостей
С' = С\ + С2.
Напряжение на зажимах батареи из двух параллельно соединенных конденсаторов
Г 7 — R — _ 3^ /п\
2CCl + C2Cl-hC2' '
Подставляя (1) в (2), получаем
2CjC2?7i
(^1 + С2)
гт 2 4 5 • Ю-20 Ф2 • 220 В
tf2 = — - =108,6 В.
92 1О20 Ф2
Ответ'. t/2= 108,6 В.
-
Заряд конденсатора 1 мкКл, площадь пластин 100 см2, зазор между пластинками заполнен слюдой. Определить объемную плотность энергии поля конденсатора и силу притяжения пластин.
Дано: 6=Ю 6 Кл; 5= 10“2 м2; е=6.
Найти: >v; F.

(1)
Решение. Сила притяжения между двумя разноименно заряженными обкладками конденсатора уг .“о£2 5 ” 2
где Е — напряженность поля конденсатора; S — площадь обкладок конденсатора; е — диэлектрическая проницаемость слюды; Eq — электрическая постоянная.

(2)
Напряженность однородного поля плоского конденсатора _ ff Q Е==. ££q EEqS
где o=QIS — поверхностная плотность заряда. Подставляя (2) в (1), получаем
о2 Ю“12 Кл2
— = 0,94 Н. 2&£qS 2 6 8,85 10“12 Ф/м 10“2 м2
Объемная плотность энергии электрического поля

(3)
££qE2
W= — .
2
Подставляя (2) в (3), получаем
Q2 ю12 Кл2 -
w=——w=- —- = 94,2 Дж/м3.
2££0S2 2 • 6 8,85 10“12 Ф/м 10“* м4
Ответ: J’=0,94 Н; w=94,2 Дж/м.
-
В медном проводнике сечением 6 мм и длиной 5 м течет ток. За 1 мин в проводнике выделяется 18 Дж теплоты. Определить напряженность поля, плотность и силу электрического тока в проводнике.
Дано: 5=6 • 106 м2; 1=5 м; /=60 с; Q= 18 Дж; р = 1,7 • 10 8 Ом ■ м.
Найти: £; j; J.
Решение. Для решения задачи используем законы Ома и Джоуля — Ленца. Закон Ома в дифференциальной форме имеет вид
(о где j — плотность тока; Е — напряженность доля; у — удельная проводимость.
Закон Джоуля — Ленца
Q^Rt. (2)
Здесь J — сила тока, t — время,
R=p' (3)
д
— сопротивление проводника, где р, I, S — удельное сопротивление, длина и площадь поперечного сечения проводника соответственно.
Силу тока J находим из (2) с учетом (3):
т [q [qS I 18 Дж 6 10-6 м2
J= /—= / ; 7= -=4,6 A.
у Rt у pit у 1,7 10 8 Ом м 5 м 60 с
По определению, плотность тока равна j=J[S\
j=4,6 А/(6 • 10"6 м2) = 7,7 • 105 А/м2.
Напряженность поля в проводнике определим из (1), учитывая, что у=\1р.
E=j- р; Е=7,7 • 105 А/м2 • 1,7 КГ8 Ом • м=1,3 • 10'2 В/м.
Ответ: Е=1,3 10“2 В/м; J=4,6 A; 7=7,7 ■ 105 А/м2.
-
Внутреннее сопротивление аккумулятора 2 Ом. При замыкании его одним резистором сила тока равна 4 А, при замыкании другим — 2 А. Во внешней цепи в обоих случаях выделяется одинаковая мощность. Определить электродвижущую силу аккумулятора и внешние сопротивления.
Дано: г-2 Ом; 7] = 4 A; J2—2 A; NX=N2.
Найти: <5 ; 2^; R2-
Решение. Закон Ома для замкнутой (полной) цепи имеет вид

где г — внутреннее сопротивление источника тока; & — э. д. с. аккумулятора; R}iiR2 — внешние сопротивления цепей.
Уравнения (1) представим в виде
<5=Л(А, + г); 6=Л№+г). (2)
Из равенства> (2) следует, что
71(А1+г)=Л№+г). (3)
Мощность, выделяемая во внешней цепи в первом и втором случаях, соответственно равна
N2=JiR2.
Из условия равенства мощностей следует, что

Решая совместно уравнения (3) и (4), получаем

(4)
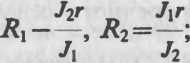

(5)
Л 2 А 2 Ом , _ Л 4 А • 2 Ом л _
— = 1 Ом, R2= = 4 Ом.
4 А 2 А
Подставляя (5) в (2), получаем
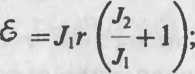 5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
Ответ: & = 12 В; Rt= 1 Ом; Л2 = 4 Ом.
-
Электродвижущая сила батареи равна 20 В. Коэффициент полезного действия батареи составляет 0,8 при силе тока 4 А. Чему равно внутреннее сопротивление батареи?
Дано: £ =20 В; >7 = 0,8; .7=4 А.
Найти: г.
Решение. Коэффициент полезного действия источника тока t] равен отношению падения напряжения во внешней цепи к его электродвижущей силе.
откуда
(2)
Используя выражение закона Ома для замкнутой цепи J= £/(Л+г), получаем
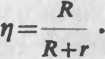
Подставляя (2) в (3) и выполняя преобразования, находим
ё(1-п) 20 в (1-0,8)
г= : г= =1 Ом.
Ответ: г— 1 Ом.
-
По двум бесконечно длинным прямолинейным проводникам, находящимся на расстоянии 50 см друг от друга, в одном направлении текут токи J\ и J2 силой по 5 А. Между проводниками на расстоянии 30 см от первого расположен кольцевой проводник с током J3 силой 5 А (рис. 3). Радиус кольца 20 см. Определить индукцию и напряженность магнитного поля, создаваемого токами в центре кольцевого проводника.
Дано: J1=J2=J3=J=5 А; ^=0,2 м; г3=0,2 м.
Найти: В\ Н.
Решение. В соответствии с принципом суперпозиции индукция результирующего магнитного поля в точке А равна
В = Bj 4-Вг + В3, (1)
где Bi и В2 — индукции полей, создаваемых соответственно токами Ji и J2, направленными за плоскость рисунка; Вз — индукция поля, создаваемая кольцевым током. Как видно из рис. 3, векторы В) и Bi направлены по одной прямой в противоположные стороны, поэтому их сумма В, 4-82 = 812 равна по модулю
В{2—В2 — Bi. (2)

(3)
Индукция поля, создаваемого бесконечно длинным проводником с током,

где До — магнитная постоянная; д — магнитная проницаемость
о\——; В2———,
2nr\ 2itr2
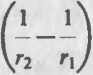





п л12=——
2л
5>
1 ... 4 5 6 7 8 9 10 11 12
E=Ej Ч-Ез.
По теореме косинусов
Е=у/Ё11+ё(+2Ё1 ' £? • cos 2а. (2)
Напряженность поля точечного заряда Q
E=QI(4nEE0r2)f
где е — диэлектрическая проницаемость; Ео — электрическая постоянная; г — расстояние от заряда до точки поля, в которой определяется его напряженность. Заряды 61 и Ол отрицательны, следовательно, векторы его Ет и Е2 направлены по линиям напряженности к зарядам. По условию заряды Q\ — Q2 расположены на одинаковом расстоянии от точки Л, поэтому ЕХ=Е2. Следовательно, формула (2) принимает вид Е=2ЕХ • cos а, где cosa—h/r^
h=OA=^rl-rll4;
h=-J(5 ■ 10'2 м2)2—(4 ' IO"2 м)2 = 3 • 10'2 м.
Тогда напряженность в точке А
2Qi h
^=—
47Г££оГ^

=480 В/м.
2 9 1(Г9 Кл 3 10"2 м
4 3,14 81 8,85 10"12 Ф/м (0,05)3 м2
Потенциал ф, создаваемый системой точечных зарядов в данной точке поля, равен алгебраической сумме потенциалов, создава-
емых каждым из зарядов ср = £ (р±. Потенциал ср результирующе- 1"1 т-г
го поля в точке А равен (p = cpi + cp2- Потенциал поля, создава
емого точечным зарядом, ф=(2/(47гее0г). Следовательно,
Ci 0.2 201
= ,+ <р2=- ;
47Г££ог1 4Я££оГ2 4Я££оГ1
4 3,14 81 8,85 10’12 Ф/м 5 10'2
Ответ’. £=480 В/м; (р — — 40 В.
-
Заряд 1 нКл переносится в воздухе из точки, находящейся на расстоянии 1 м от бесконечно длинной равномерно заряженной нити, в точку на расстоянии 10 см от нее. Определить работу, совершаемую против сил поля, если линейная плотность заряда нити 1 мкКл/м. Какая работа совершается на последних 10 см пути?
Дано: го=О,1 м; п = 1 м; г2=0,2 м; Q=1 109 Кл; е=1; т= 1 • 10-6 Кл/м.
Найти: А2.
Решение. Работа внешней силы по перемещению заряда Q из точки поля с потенциалом (pt в точку с потенциалом <р0 равна
^ = С(фоФ1). О)
Бесконечная равномерно заряженная нить с линейной плотностью заряда т создает аксиально-симметричное поле напряженностью £=т/(27гее0г). Напряженность и потенциал этого поля d
связаны соотношением £= , откуда d
Edr. Разность
dr
потенциалов точек поля на расстоянии г, и г0 от нити
Г0


Фо-ф.= -
£dr =
т f dr т г*
-= In
2леео J г 2пеео го
г

И In
Го
i
Т
Фо-<Р1 = П
2Л6£о

(2)
Г2
(Р0-(Р2 = — Ь
2я££0 г0
Подставляя в формулу (1) найденное выражение для разности потенциалов из (2), определим работу, совершаемую внешними силами по перемещению заряда из точки, находящейся на расстоянии 1 м, до точки, расположенной на расстоянии 0,1 м от нити:
2л££о го’

• 10'J Дж.
, 1 • 10’9 Кл 1 • 1О’€ Кл/м In 10 , .
А1 = — =4,1
2 3,14 8,85 1012 Ф/м
„ 1 • 10"9 ■ 1 • 10€ In 10
Вычислим на калькуляторе выражение —■ по
2 3,14 8,85 10-12
программе
1[вп|9[7ч1И 1®б[Н10 югаа 2 0EI008,85R 1|вп] 12I/-/IR
Показания индикатора: 4,14087 10 5, т. е. 4,1 • 10“5 Дж.
Работа по перемещению заряда на последних 10 см пути равна
С т, Г2
Л2= In -;
2леео г0
, 1 • Ю 9 Кл 10 б Кл/м 1п2 , _ _ , „
Л2 = 7 - = 1,25 • 10'5 Дж.
2 3,14 8,85 10-12 Ф/м
Ответ: Л1 = 4,1 ' 10 5 Дж; Л2=1,25 • 10 5 Дж.
-
К одной из обкладок плоского конденсатора прилегает стеклянная плоскопараллельная пластинка (£1 = 7) толщиной 9 мм. После того как конденсатор отключили от источника напряжения 220 В и вынули стеклянную пластинку, между обкладками установилась разность потенциалов 976 В. Определить зазор между обкладками и отношение конечной и начальной энергии конденсатора.
Дано: С7!=220 В; (72=976 В; dj = 9 103 м; £1 = 7; е2=1.
Найти: do; W\/W2.
Решение. После отключения конденсатора и удаления стеклянной пластинки заряд на его обкладках остается неизменным, т. е. выполняется равенство
Cit7i = C2t/2, (1)
где С\ и С2 — электроемкости конденсатора в начальном и конечном случае.
По условию конденсатор вначале является слоистым и его электроемкость определяется по формуле
Eg ‘ S

(2)
G= —
di dodi
— +
£1 Е2
где 5 — площадь обкладок; d0 — зазор между ними, dx — толщина стеклянной пластинки, Ej и е2 — диэлектрические проницаемости стекла и воздуха соответственно.

E2£oS
После удаления стеклянной пластинки электроемкость конденсатора
(3)
Подставляя (2) и (3) в (1), получим
£о5С/1 £2£o5L/2
d\ do d\ dQ
£1 £2
откуда

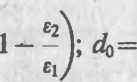






“о—
U2-Ui
976 В 9 IO-3
(976 - 220) В
м
1-’|=1 • 10’2 7/
M.
Начальная и конечная энергии конденсатора
CiU2. C2u22
W\=—; W2=—.
2 2
Тогда отношение этих энергий W2/Wi = C2U2/(CiUl). Учитывая (1), получим
W2 U2 W2 976 В . . .
——• — = 4 44
Wi Uif Wi 220 В
Ответ: do=l ' Ю“2 м; FF2/FFi=4,44.
-
Батарею из двух конденсаторов емкостью 400 и 500 пФ соединили последовательно и включили в сеть с напряжением 220 В. Потом батарею отключили от сети, конденсаторы разъединили и соединили параллельно обкладками, имеющими одноименные заряды. Каким будет напряжение на зажимах полученной батареи?
Дано: £7j = 220 В; Cj=400 пФ; С2=500 пФ.
Найти: U2.
Решение. У последовательно соединенных конденсаторов заряды на обкладках равны по модулю 61 = 62=6 и заряд батареи равен заряду одного конденсатора. Емкость батареи последовательно соединенных конденсаторов определяется по формуле п
1/С= £ 1/С«. Для батареи из двух конденсаторов
С=С, • С2/(С, + С2),
а их заряд
6 = СС/1 = С1С2С/1/(С1 + С2). (1)
При отключении конденсаторов их заряд сохраняется. У параллельно соединенных конденсаторов заряд батареи равен сумме зарядов конденсаторов 6=61 + 62» а емкость — сумме емкостей
С' = С\ + С2.
Напряжение на зажимах батареи из двух параллельно соединенных конденсаторов
Г 7 — R — _ 3^ /п\
2CCl + C2Cl-hC2' '
Подставляя (1) в (2), получаем
2CjC2?7i
(^1 + С2)
гт 2 4 5 • Ю-20 Ф2 • 220 В
tf2 = — - =108,6 В.
92 1О20 Ф2
Ответ'. t/2= 108,6 В.
-
Заряд конденсатора 1 мкКл, площадь пластин 100 см2, зазор между пластинками заполнен слюдой. Определить объемную плотность энергии поля конденсатора и силу притяжения пластин.
Дано: 6=Ю 6 Кл; 5= 10“2 м2; е=6.
Найти: >v; F.

(1)
Решение. Сила притяжения между двумя разноименно заряженными обкладками конденсатора уг .“о£2 5 ” 2
где Е — напряженность поля конденсатора; S — площадь обкладок конденсатора; е — диэлектрическая проницаемость слюды; Eq — электрическая постоянная.

(2)
Напряженность однородного поля плоского конденсатора _ ff Q Е==. ££q EEqS
где o=QIS — поверхностная плотность заряда. Подставляя (2) в (1), получаем
о2 Ю“12 Кл2
— = 0,94 Н. 2&£qS 2 6 8,85 10“12 Ф/м 10“2 м2
Объемная плотность энергии электрического поля

(3)
££qE2
W= — .
2
Подставляя (2) в (3), получаем
Q2 ю12 Кл2 -
w=——w=- —- = 94,2 Дж/м3.
2££0S2 2 • 6 8,85 10“12 Ф/м 10“* м4
Ответ: J’=0,94 Н; w=94,2 Дж/м.
-
В медном проводнике сечением 6 мм и длиной 5 м течет ток. За 1 мин в проводнике выделяется 18 Дж теплоты. Определить напряженность поля, плотность и силу электрического тока в проводнике.
Дано: 5=6 • 106 м2; 1=5 м; /=60 с; Q= 18 Дж; р = 1,7 • 10 8 Ом ■ м.
Найти: £; j; J.
Решение. Для решения задачи используем законы Ома и Джоуля — Ленца. Закон Ома в дифференциальной форме имеет вид
(о где j — плотность тока; Е — напряженность доля; у — удельная проводимость.
Закон Джоуля — Ленца
Q^Rt. (2)
Здесь J — сила тока, t — время,
R=p' (3)
д
— сопротивление проводника, где р, I, S — удельное сопротивление, длина и площадь поперечного сечения проводника соответственно.
Силу тока J находим из (2) с учетом (3):
т [q [qS I 18 Дж 6 10-6 м2
J= /—= / ; 7= -=4,6 A.
у Rt у pit у 1,7 10 8 Ом м 5 м 60 с
По определению, плотность тока равна j=J[S\
j=4,6 А/(6 • 10"6 м2) = 7,7 • 105 А/м2.
Напряженность поля в проводнике определим из (1), учитывая, что у=\1р.
E=j- р; Е=7,7 • 105 А/м2 • 1,7 КГ8 Ом • м=1,3 • 10'2 В/м.
Ответ: Е=1,3 10“2 В/м; J=4,6 A; 7=7,7 ■ 105 А/м2.
-
Внутреннее сопротивление аккумулятора 2 Ом. При замыкании его одним резистором сила тока равна 4 А, при замыкании другим — 2 А. Во внешней цепи в обоих случаях выделяется одинаковая мощность. Определить электродвижущую силу аккумулятора и внешние сопротивления.
Дано: г-2 Ом; 7] = 4 A; J2—2 A; NX=N2.
Найти: <5 ; 2^; R2-
Решение. Закон Ома для замкнутой (полной) цепи имеет вид

где г — внутреннее сопротивление источника тока; & — э. д. с. аккумулятора; R}iiR2 — внешние сопротивления цепей.
Уравнения (1) представим в виде
<5=Л(А, + г); 6=Л№+г). (2)
Из равенства> (2) следует, что
71(А1+г)=Л№+г). (3)
Мощность, выделяемая во внешней цепи в первом и втором случаях, соответственно равна
N2=JiR2.
Из условия равенства мощностей следует, что

Решая совместно уравнения (3) и (4), получаем

(4)
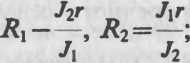

(5)
Л 2 А 2 Ом , _ Л 4 А • 2 Ом л _
— = 1 Ом, R2= = 4 Ом.
4 А 2 А
Подставляя (5) в (2), получаем
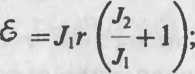 5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
Ответ: & = 12 В; Rt= 1 Ом; Л2 = 4 Ом.
-
Электродвижущая сила батареи равна 20 В. Коэффициент полезного действия батареи составляет 0,8 при силе тока 4 А. Чему равно внутреннее сопротивление батареи?
Дано: £ =20 В; >7 = 0,8; .7=4 А.
Найти: г.
Решение. Коэффициент полезного действия источника тока t] равен отношению падения напряжения во внешней цепи к его электродвижущей силе.
откуда
(2)
Используя выражение закона Ома для замкнутой цепи J= £/(Л+г), получаем
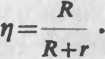
Подставляя (2) в (3) и выполняя преобразования, находим
ё(1-п) 20 в (1-0,8)
г= : г= =1 Ом.
Ответ: г— 1 Ом.
-
По двум бесконечно длинным прямолинейным проводникам, находящимся на расстоянии 50 см друг от друга, в одном направлении текут токи J\ и J2 силой по 5 А. Между проводниками на расстоянии 30 см от первого расположен кольцевой проводник с током J3 силой 5 А (рис. 3). Радиус кольца 20 см. Определить индукцию и напряженность магнитного поля, создаваемого токами в центре кольцевого проводника.
Дано: J1=J2=J3=J=5 А; ^=0,2 м; г3=0,2 м.
Найти: В\ Н.
Решение. В соответствии с принципом суперпозиции индукция результирующего магнитного поля в точке А равна
В = Bj 4-Вг + В3, (1)
где Bi и В2 — индукции полей, создаваемых соответственно токами Ji и J2, направленными за плоскость рисунка; Вз — индукция поля, создаваемая кольцевым током. Как видно из рис. 3, векторы В) и Bi направлены по одной прямой в противоположные стороны, поэтому их сумма В, 4-82 = 812 равна по модулю
В{2—В2 — Bi. (2)

(3)
Индукция поля, создаваемого бесконечно длинным проводником с током,

где До — магнитная постоянная; д — магнитная проницаемость
о\——; В2———,
2nr\ 2itr2
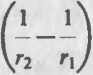





п л12=——
2л
5>
1 ... 4 5 6 7 8 9 10 11 12
E=Ej Ч-Ез.
По теореме косинусов
Е=у/Ё11+ё(+2Ё1 ' £? • cos 2а. (2)
Напряженность поля точечного заряда Q
E=QI(4nEE0r2)f
где е — диэлектрическая проницаемость; Ео — электрическая постоянная; г — расстояние от заряда до точки поля, в которой определяется его напряженность. Заряды 61 и Ол отрицательны, следовательно, векторы его Ет и Е2 направлены по линиям напряженности к зарядам. По условию заряды Q\ — Q2 расположены на одинаковом расстоянии от точки Л, поэтому ЕХ=Е2. Следовательно, формула (2) принимает вид Е=2ЕХ • cos а, где cosa—h/r^
h=OA=^rl-rll4;
h=-J(5 ■ 10'2 м2)2—(4 ' IO"2 м)2 = 3 • 10'2 м.
Тогда напряженность в точке А
2Qi h
^=—
47Г££оГ^

=480 В/м.
2 9 1(Г9 Кл 3 10"2 м
4 3,14 81 8,85 10"12 Ф/м (0,05)3 м2
Потенциал ф, создаваемый системой точечных зарядов в данной точке поля, равен алгебраической сумме потенциалов, создава-
емых каждым из зарядов ср = £ (р±. Потенциал ср результирующе- 1"1 т-г
го поля в точке А равен (p = cpi + cp2- Потенциал поля, создава
емого точечным зарядом, ф=(2/(47гее0г). Следовательно,
Ci 0.2 201
= ,+ <р2=- ;
47Г££ог1 4Я££оГ2 4Я££оГ1
4 3,14 81 8,85 10’12 Ф/м 5 10'2
Ответ’. £=480 В/м; (р — — 40 В.
-
Заряд 1 нКл переносится в воздухе из точки, находящейся на расстоянии 1 м от бесконечно длинной равномерно заряженной нити, в точку на расстоянии 10 см от нее. Определить работу, совершаемую против сил поля, если линейная плотность заряда нити 1 мкКл/м. Какая работа совершается на последних 10 см пути?
Дано: го=О,1 м; п = 1 м; г2=0,2 м; Q=1 109 Кл; е=1; т= 1 • 10-6 Кл/м.
Найти: А2.
Решение. Работа внешней силы по перемещению заряда Q из точки поля с потенциалом (pt в точку с потенциалом <р0 равна
^ = С(фоФ1). О)
Бесконечная равномерно заряженная нить с линейной плотностью заряда т создает аксиально-симметричное поле напряженностью £=т/(27гее0г). Напряженность и потенциал этого поля d
связаны соотношением £= , откуда d
Edr. Разность
dr
потенциалов точек поля на расстоянии г, и г0 от нити
Г0


Фо-ф.= -
£dr =
т f dr т г*
-= In
2леео J г 2пеео го
г

И In
Го
i
Т
Фо-<Р1 = П
2Л6£о

(2)
Г2
(Р0-(Р2 = — Ь
2я££0 г0
Подставляя в формулу (1) найденное выражение для разности потенциалов из (2), определим работу, совершаемую внешними силами по перемещению заряда из точки, находящейся на расстоянии 1 м, до точки, расположенной на расстоянии 0,1 м от нити:
2л££о го’

• 10'J Дж.
, 1 • 10’9 Кл 1 • 1О’€ Кл/м In 10 , .
А1 = — =4,1
2 3,14 8,85 1012 Ф/м
„ 1 • 10"9 ■ 1 • 10€ In 10
Вычислим на калькуляторе выражение —■ по
2 3,14 8,85 10-12
программе
1[вп|9[7ч1И 1®б[Н10 югаа 2 0EI008,85R 1|вп] 12I/-/IR
Показания индикатора: 4,14087 10 5, т. е. 4,1 • 10“5 Дж.
Работа по перемещению заряда на последних 10 см пути равна
С т, Г2
Л2= In -;
2леео г0
, 1 • Ю 9 Кл 10 б Кл/м 1п2 , _ _ , „
Л2 = 7 - = 1,25 • 10'5 Дж.
2 3,14 8,85 10-12 Ф/м
Ответ: Л1 = 4,1 ' 10 5 Дж; Л2=1,25 • 10 5 Дж.
-
К одной из обкладок плоского конденсатора прилегает стеклянная плоскопараллельная пластинка (£1 = 7) толщиной 9 мм. После того как конденсатор отключили от источника напряжения 220 В и вынули стеклянную пластинку, между обкладками установилась разность потенциалов 976 В. Определить зазор между обкладками и отношение конечной и начальной энергии конденсатора.
Дано: С7!=220 В; (72=976 В; dj = 9 103 м; £1 = 7; е2=1.
Найти: do; W\/W2.
Решение. После отключения конденсатора и удаления стеклянной пластинки заряд на его обкладках остается неизменным, т. е. выполняется равенство
Cit7i = C2t/2, (1)
где С\ и С2 — электроемкости конденсатора в начальном и конечном случае.
По условию конденсатор вначале является слоистым и его электроемкость определяется по формуле
Eg ‘ S

(2)
G= —
di dodi
— +
£1 Е2
где 5 — площадь обкладок; d0 — зазор между ними, dx — толщина стеклянной пластинки, Ej и е2 — диэлектрические проницаемости стекла и воздуха соответственно.

E2£oS
После удаления стеклянной пластинки электроемкость конденсатора
(3)
Подставляя (2) и (3) в (1), получим
£о5С/1 £2£o5L/2
d\ do d\ dQ
£1 £2
откуда

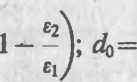






“о—
U2-Ui
976 В 9 IO-3
(976 - 220) В
м
1-’|=1 • 10’2 7/
M.
Начальная и конечная энергии конденсатора
CiU2. C2u22
W\=—; W2=—.
2 2
Тогда отношение этих энергий W2/Wi = C2U2/(CiUl). Учитывая (1), получим
W2 U2 W2 976 В . . .
——• — = 4 44
Wi Uif Wi 220 В
Ответ: do=l ' Ю“2 м; FF2/FFi=4,44.
-
Батарею из двух конденсаторов емкостью 400 и 500 пФ соединили последовательно и включили в сеть с напряжением 220 В. Потом батарею отключили от сети, конденсаторы разъединили и соединили параллельно обкладками, имеющими одноименные заряды. Каким будет напряжение на зажимах полученной батареи?
Дано: £7j = 220 В; Cj=400 пФ; С2=500 пФ.
Найти: U2.
Решение. У последовательно соединенных конденсаторов заряды на обкладках равны по модулю 61 = 62=6 и заряд батареи равен заряду одного конденсатора. Емкость батареи последовательно соединенных конденсаторов определяется по формуле п
1/С= £ 1/С«. Для батареи из двух конденсаторов
С=С, • С2/(С, + С2),
а их заряд
6 = СС/1 = С1С2С/1/(С1 + С2). (1)
При отключении конденсаторов их заряд сохраняется. У параллельно соединенных конденсаторов заряд батареи равен сумме зарядов конденсаторов 6=61 + 62» а емкость — сумме емкостей
С' = С\ + С2.
Напряжение на зажимах батареи из двух параллельно соединенных конденсаторов
Г 7 — R — _ 3^ /п\
2CCl + C2Cl-hC2' '
Подставляя (1) в (2), получаем
2CjC2?7i
(^1 + С2)
гт 2 4 5 • Ю-20 Ф2 • 220 В
tf2 = — - =108,6 В.
92 1О20 Ф2
Ответ'. t/2= 108,6 В.
-
Заряд конденсатора 1 мкКл, площадь пластин 100 см2, зазор между пластинками заполнен слюдой. Определить объемную плотность энергии поля конденсатора и силу притяжения пластин.
Дано: 6=Ю 6 Кл; 5= 10“2 м2; е=6.
Найти: >v; F.

(1)
Решение. Сила притяжения между двумя разноименно заряженными обкладками конденсатора уг .“о£2 5 ” 2
где Е — напряженность поля конденсатора; S — площадь обкладок конденсатора; е — диэлектрическая проницаемость слюды; Eq — электрическая постоянная.

(2)
Напряженность однородного поля плоского конденсатора _ ff Q Е==. ££q EEqS
где o=QIS — поверхностная плотность заряда. Подставляя (2) в (1), получаем
о2 Ю“12 Кл2
— = 0,94 Н. 2&£qS 2 6 8,85 10“12 Ф/м 10“2 м2
Объемная плотность энергии электрического поля

(3)
££qE2
W= — .
2
Подставляя (2) в (3), получаем
Q2 ю12 Кл2 -
w=——w=- —- = 94,2 Дж/м3.
2££0S2 2 • 6 8,85 10“12 Ф/м 10“* м4
Ответ: J’=0,94 Н; w=94,2 Дж/м.
-
В медном проводнике сечением 6 мм и длиной 5 м течет ток. За 1 мин в проводнике выделяется 18 Дж теплоты. Определить напряженность поля, плотность и силу электрического тока в проводнике.
Дано: 5=6 • 106 м2; 1=5 м; /=60 с; Q= 18 Дж; р = 1,7 • 10 8 Ом ■ м.
Найти: £; j; J.
Решение. Для решения задачи используем законы Ома и Джоуля — Ленца. Закон Ома в дифференциальной форме имеет вид
(о где j — плотность тока; Е — напряженность доля; у — удельная проводимость.
Закон Джоуля — Ленца
Q^Rt. (2)
Здесь J — сила тока, t — время,
R=p' (3)
д
— сопротивление проводника, где р, I, S — удельное сопротивление, длина и площадь поперечного сечения проводника соответственно.
Силу тока J находим из (2) с учетом (3):
т [q [qS I 18 Дж 6 10-6 м2
J= /—= / ; 7= -=4,6 A.
у Rt у pit у 1,7 10 8 Ом м 5 м 60 с
По определению, плотность тока равна j=J[S\
j=4,6 А/(6 • 10"6 м2) = 7,7 • 105 А/м2.
Напряженность поля в проводнике определим из (1), учитывая, что у=\1р.
E=j- р; Е=7,7 • 105 А/м2 • 1,7 КГ8 Ом • м=1,3 • 10'2 В/м.
Ответ: Е=1,3 10“2 В/м; J=4,6 A; 7=7,7 ■ 105 А/м2.
-
Внутреннее сопротивление аккумулятора 2 Ом. При замыкании его одним резистором сила тока равна 4 А, при замыкании другим — 2 А. Во внешней цепи в обоих случаях выделяется одинаковая мощность. Определить электродвижущую силу аккумулятора и внешние сопротивления.
Дано: г-2 Ом; 7] = 4 A; J2—2 A; NX=N2.
Найти: <5 ; 2^; R2-
Решение. Закон Ома для замкнутой (полной) цепи имеет вид

где г — внутреннее сопротивление источника тока; & — э. д. с. аккумулятора; R}iiR2 — внешние сопротивления цепей.
Уравнения (1) представим в виде
<5=Л(А, + г); 6=Л№+г). (2)
Из равенства> (2) следует, что
71(А1+г)=Л№+г). (3)
Мощность, выделяемая во внешней цепи в первом и втором случаях, соответственно равна
N2=JiR2.
Из условия равенства мощностей следует, что

Решая совместно уравнения (3) и (4), получаем

(4)
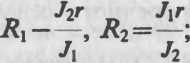

(5)
Л 2 А 2 Ом , _ Л 4 А • 2 Ом л _
— = 1 Ом, R2= = 4 Ом.
4 А 2 А
Подставляя (5) в (2), получаем
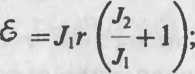 5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
Ответ: & = 12 В; Rt= 1 Ом; Л2 = 4 Ом.
-
Электродвижущая сила батареи равна 20 В. Коэффициент полезного действия батареи составляет 0,8 при силе тока 4 А. Чему равно внутреннее сопротивление батареи?
Дано: £ =20 В; >7 = 0,8; .7=4 А.
Найти: г.
Решение. Коэффициент полезного действия источника тока t] равен отношению падения напряжения во внешней цепи к его электродвижущей силе.
откуда
(2)
Используя выражение закона Ома для замкнутой цепи J= £/(Л+г), получаем
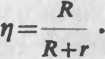
Подставляя (2) в (3) и выполняя преобразования, находим
ё(1-п) 20 в (1-0,8)
г= : г= =1 Ом.
Ответ: г— 1 Ом.
-
По двум бесконечно длинным прямолинейным проводникам, находящимся на расстоянии 50 см друг от друга, в одном направлении текут токи J\ и J2 силой по 5 А. Между проводниками на расстоянии 30 см от первого расположен кольцевой проводник с током J3 силой 5 А (рис. 3). Радиус кольца 20 см. Определить индукцию и напряженность магнитного поля, создаваемого токами в центре кольцевого проводника.
Дано: J1=J2=J3=J=5 А; ^=0,2 м; г3=0,2 м.
Найти: В\ Н.
Решение. В соответствии с принципом суперпозиции индукция результирующего магнитного поля в точке А равна
В = Bj 4-Вг + В3, (1)
где Bi и В2 — индукции полей, создаваемых соответственно токами Ji и J2, направленными за плоскость рисунка; Вз — индукция поля, создаваемая кольцевым током. Как видно из рис. 3, векторы В) и Bi направлены по одной прямой в противоположные стороны, поэтому их сумма В, 4-82 = 812 равна по модулю
В{2—В2 — Bi. (2)

(3)
Индукция поля, создаваемого бесконечно длинным проводником с током,

где До — магнитная постоянная; д — магнитная проницаемость
о\——; В2———,
2nr\ 2itr2
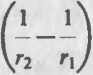





п л12=——
2л
5>
1 ... 4 5 6 7 8 9 10 11 12
E=Ej Ч-Ез.
По теореме косинусов
Е=у/Ё11+ё(+2Ё1 ' £? • cos 2а. (2)
Напряженность поля точечного заряда Q
E=QI(4nEE0r2)f
где е — диэлектрическая проницаемость; Ео — электрическая постоянная; г — расстояние от заряда до точки поля, в которой определяется его напряженность. Заряды 61 и Ол отрицательны, следовательно, векторы его Ет и Е2 направлены по линиям напряженности к зарядам. По условию заряды Q\ — Q2 расположены на одинаковом расстоянии от точки Л, поэтому ЕХ=Е2. Следовательно, формула (2) принимает вид Е=2ЕХ • cos а, где cosa—h/r^
h=OA=^rl-rll4;
h=-J(5 ■ 10'2 м2)2—(4 ' IO"2 м)2 = 3 • 10'2 м.
Тогда напряженность в точке А
2Qi h
^=—
47Г££оГ^

=480 В/м.
2 9 1(Г9 Кл 3 10"2 м
4 3,14 81 8,85 10"12 Ф/м (0,05)3 м2
Потенциал ф, создаваемый системой точечных зарядов в данной точке поля, равен алгебраической сумме потенциалов, создава-
емых каждым из зарядов ср = £ (р±. Потенциал ср результирующе- 1"1 т-г
го поля в точке А равен (p = cpi + cp2- Потенциал поля, создава
емого точечным зарядом, ф=(2/(47гее0г). Следовательно,
Ci 0.2 201
= ,+ <р2=- ;
47Г££ог1 4Я££оГ2 4Я££оГ1
4 3,14 81 8,85 10’12 Ф/м 5 10'2
Ответ’. £=480 В/м; (р — — 40 В.
-
Заряд 1 нКл переносится в воздухе из точки, находящейся на расстоянии 1 м от бесконечно длинной равномерно заряженной нити, в точку на расстоянии 10 см от нее. Определить работу, совершаемую против сил поля, если линейная плотность заряда нити 1 мкКл/м. Какая работа совершается на последних 10 см пути?
Дано: го=О,1 м; п = 1 м; г2=0,2 м; Q=1 109 Кл; е=1; т= 1 • 10-6 Кл/м.
Найти: А2.
Решение. Работа внешней силы по перемещению заряда Q из точки поля с потенциалом (pt в точку с потенциалом <р0 равна
^ = С(фоФ1). О)
Бесконечная равномерно заряженная нить с линейной плотностью заряда т создает аксиально-симметричное поле напряженностью £=т/(27гее0г). Напряженность и потенциал этого поля d
связаны соотношением £= , откуда d
Edr. Разность
dr
потенциалов точек поля на расстоянии г, и г0 от нити
Г0


Фо-ф.= -
£dr =
т f dr т г*
-= In
2леео J г 2пеео го
г

И In
Го
i
Т
Фо-<Р1 = П
2Л6£о

(2)
Г2
(Р0-(Р2 = — Ь
2я££0 г0
Подставляя в формулу (1) найденное выражение для разности потенциалов из (2), определим работу, совершаемую внешними силами по перемещению заряда из точки, находящейся на расстоянии 1 м, до точки, расположенной на расстоянии 0,1 м от нити:
2л££о го’

• 10'J Дж.
, 1 • 10’9 Кл 1 • 1О’€ Кл/м In 10 , .
А1 = — =4,1
2 3,14 8,85 1012 Ф/м
„ 1 • 10"9 ■ 1 • 10€ In 10
Вычислим на калькуляторе выражение —■ по
2 3,14 8,85 10-12
программе
1[вп|9[7ч1И 1®б[Н10 югаа 2 0EI008,85R 1|вп] 12I/-/IR
Показания индикатора: 4,14087 10 5, т. е. 4,1 • 10“5 Дж.
Работа по перемещению заряда на последних 10 см пути равна
С т, Г2
Л2= In -;
2леео г0
, 1 • Ю 9 Кл 10 б Кл/м 1п2 , _ _ , „
Л2 = 7 - = 1,25 • 10'5 Дж.
2 3,14 8,85 10-12 Ф/м
Ответ: Л1 = 4,1 ' 10 5 Дж; Л2=1,25 • 10 5 Дж.
-
К одной из обкладок плоского конденсатора прилегает стеклянная плоскопараллельная пластинка (£1 = 7) толщиной 9 мм. После того как конденсатор отключили от источника напряжения 220 В и вынули стеклянную пластинку, между обкладками установилась разность потенциалов 976 В. Определить зазор между обкладками и отношение конечной и начальной энергии конденсатора.
Дано: С7!=220 В; (72=976 В; dj = 9 103 м; £1 = 7; е2=1.
Найти: do; W\/W2.
Решение. После отключения конденсатора и удаления стеклянной пластинки заряд на его обкладках остается неизменным, т. е. выполняется равенство
Cit7i = C2t/2, (1)
где С\ и С2 — электроемкости конденсатора в начальном и конечном случае.
По условию конденсатор вначале является слоистым и его электроемкость определяется по формуле
Eg ‘ S

(2)
G= —
di dodi
— +
£1 Е2
где 5 — площадь обкладок; d0 — зазор между ними, dx — толщина стеклянной пластинки, Ej и е2 — диэлектрические проницаемости стекла и воздуха соответственно.

E2£oS
После удаления стеклянной пластинки электроемкость конденсатора
(3)
Подставляя (2) и (3) в (1), получим
£о5С/1 £2£o5L/2
d\ do d\ dQ
£1 £2
откуда

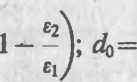






“о—
U2-Ui
976 В 9 IO-3
(976 - 220) В
м
1-’|=1 • 10’2 7/
M.
Начальная и конечная энергии конденсатора
CiU2. C2u22
W\=—; W2=—.
2 2
Тогда отношение этих энергий W2/Wi = C2U2/(CiUl). Учитывая (1), получим
W2 U2 W2 976 В . . .
——• — = 4 44
Wi Uif Wi 220 В
Ответ: do=l ' Ю“2 м; FF2/FFi=4,44.
-
Батарею из двух конденсаторов емкостью 400 и 500 пФ соединили последовательно и включили в сеть с напряжением 220 В. Потом батарею отключили от сети, конденсаторы разъединили и соединили параллельно обкладками, имеющими одноименные заряды. Каким будет напряжение на зажимах полученной батареи?
Дано: £7j = 220 В; Cj=400 пФ; С2=500 пФ.
Найти: U2.
Решение. У последовательно соединенных конденсаторов заряды на обкладках равны по модулю 61 = 62=6 и заряд батареи равен заряду одного конденсатора. Емкость батареи последовательно соединенных конденсаторов определяется по формуле п
1/С= £ 1/С«. Для батареи из двух конденсаторов
С=С, • С2/(С, + С2),
а их заряд
6 = СС/1 = С1С2С/1/(С1 + С2). (1)
При отключении конденсаторов их заряд сохраняется. У параллельно соединенных конденсаторов заряд батареи равен сумме зарядов конденсаторов 6=61 + 62» а емкость — сумме емкостей
С' = С\ + С2.
Напряжение на зажимах батареи из двух параллельно соединенных конденсаторов
Г 7 — R — _ 3^ /п\
2CCl + C2Cl-hC2' '
Подставляя (1) в (2), получаем
2CjC2?7i
(^1 + С2)
гт 2 4 5 • Ю-20 Ф2 • 220 В
tf2 = — - =108,6 В.
92 1О20 Ф2
Ответ'. t/2= 108,6 В.
-
Заряд конденсатора 1 мкКл, площадь пластин 100 см2, зазор между пластинками заполнен слюдой. Определить объемную плотность энергии поля конденсатора и силу притяжения пластин.
Дано: 6=Ю 6 Кл; 5= 10“2 м2; е=6.
Найти: >v; F.

(1)
Решение. Сила притяжения между двумя разноименно заряженными обкладками конденсатора уг .“о£2 5 ” 2
где Е — напряженность поля конденсатора; S — площадь обкладок конденсатора; е — диэлектрическая проницаемость слюды; Eq — электрическая постоянная.

(2)
Напряженность однородного поля плоского конденсатора _ ff Q Е==. ££q EEqS
где o=QIS — поверхностная плотность заряда. Подставляя (2) в (1), получаем
о2 Ю“12 Кл2
— = 0,94 Н. 2&£qS 2 6 8,85 10“12 Ф/м 10“2 м2
Объемная плотность энергии электрического поля

(3)
££qE2
W= — .
2
Подставляя (2) в (3), получаем
Q2 ю12 Кл2 -
w=——w=- —- = 94,2 Дж/м3.
2££0S2 2 • 6 8,85 10“12 Ф/м 10“* м4
Ответ: J’=0,94 Н; w=94,2 Дж/м.
-
В медном проводнике сечением 6 мм и длиной 5 м течет ток. За 1 мин в проводнике выделяется 18 Дж теплоты. Определить напряженность поля, плотность и силу электрического тока в проводнике.
Дано: 5=6 • 106 м2; 1=5 м; /=60 с; Q= 18 Дж; р = 1,7 • 10 8 Ом ■ м.
Найти: £; j; J.
Решение. Для решения задачи используем законы Ома и Джоуля — Ленца. Закон Ома в дифференциальной форме имеет вид
(о где j — плотность тока; Е — напряженность доля; у — удельная проводимость.
Закон Джоуля — Ленца
Q^Rt. (2)
Здесь J — сила тока, t — время,
R=p' (3)
д
— сопротивление проводника, где р, I, S — удельное сопротивление, длина и площадь поперечного сечения проводника соответственно.
Силу тока J находим из (2) с учетом (3):
т [q [qS I 18 Дж 6 10-6 м2
J= /—= / ; 7= -=4,6 A.
у Rt у pit у 1,7 10 8 Ом м 5 м 60 с
По определению, плотность тока равна j=J[S\
j=4,6 А/(6 • 10"6 м2) = 7,7 • 105 А/м2.
Напряженность поля в проводнике определим из (1), учитывая, что у=\1р.
E=j- р; Е=7,7 • 105 А/м2 • 1,7 КГ8 Ом • м=1,3 • 10'2 В/м.
Ответ: Е=1,3 10“2 В/м; J=4,6 A; 7=7,7 ■ 105 А/м2.
-
Внутреннее сопротивление аккумулятора 2 Ом. При замыкании его одним резистором сила тока равна 4 А, при замыкании другим — 2 А. Во внешней цепи в обоих случаях выделяется одинаковая мощность. Определить электродвижущую силу аккумулятора и внешние сопротивления.
Дано: г-2 Ом; 7] = 4 A; J2—2 A; NX=N2.
Найти: <5 ; 2^; R2-
Решение. Закон Ома для замкнутой (полной) цепи имеет вид

где г — внутреннее сопротивление источника тока; & — э. д. с. аккумулятора; R}iiR2 — внешние сопротивления цепей.
Уравнения (1) представим в виде
<5=Л(А, + г); 6=Л№+г). (2)
Из равенства> (2) следует, что
71(А1+г)=Л№+г). (3)
Мощность, выделяемая во внешней цепи в первом и втором случаях, соответственно равна
N2=JiR2.
Из условия равенства мощностей следует, что

Решая совместно уравнения (3) и (4), получаем

(4)
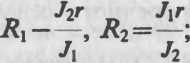

(5)
Л 2 А 2 Ом , _ Л 4 А • 2 Ом л _
— = 1 Ом, R2= = 4 Ом.
4 А 2 А
Подставляя (5) в (2), получаем
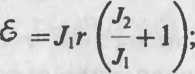 5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
Ответ: & = 12 В; Rt= 1 Ом; Л2 = 4 Ом.
-
Электродвижущая сила батареи равна 20 В. Коэффициент полезного действия батареи составляет 0,8 при силе тока 4 А. Чему равно внутреннее сопротивление батареи?
Дано: £ =20 В; >7 = 0,8; .7=4 А.
Найти: г.
Решение. Коэффициент полезного действия источника тока t] равен отношению падения напряжения во внешней цепи к его электродвижущей силе.
откуда
(2)
Используя выражение закона Ома для замкнутой цепи J= £/(Л+г), получаем
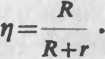
Подставляя (2) в (3) и выполняя преобразования, находим
ё(1-п) 20 в (1-0,8)
г= : г= =1 Ом.
Ответ: г— 1 Ом.
-
По двум бесконечно длинным прямолинейным проводникам, находящимся на расстоянии 50 см друг от друга, в одном направлении текут токи J\ и J2 силой по 5 А. Между проводниками на расстоянии 30 см от первого расположен кольцевой проводник с током J3 силой 5 А (рис. 3). Радиус кольца 20 см. Определить индукцию и напряженность магнитного поля, создаваемого токами в центре кольцевого проводника.
Дано: J1=J2=J3=J=5 А; ^=0,2 м; г3=0,2 м.
Найти: В\ Н.
Решение. В соответствии с принципом суперпозиции индукция результирующего магнитного поля в точке А равна
В = Bj 4-Вг + В3, (1)
где Bi и В2 — индукции полей, создаваемых соответственно токами Ji и J2, направленными за плоскость рисунка; Вз — индукция поля, создаваемая кольцевым током. Как видно из рис. 3, векторы В) и Bi направлены по одной прямой в противоположные стороны, поэтому их сумма В, 4-82 = 812 равна по модулю
В{2—В2 — Bi. (2)

(3)
Индукция поля, создаваемого бесконечно длинным проводником с током,

где До — магнитная постоянная; д — магнитная проницаемость
о\——; В2———,
2nr\ 2itr2
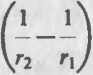





п л12=——
2л
5>
1 ... 4 5 6 7 8 9 10 11 12
E=Ej Ч-Ез.
По теореме косинусов
Е=у/Ё11+ё(+2Ё1 ' £? • cos 2а. (2)
Напряженность поля точечного заряда Q
E=QI(4nEE0r2)f
где е — диэлектрическая проницаемость; Ео — электрическая постоянная; г — расстояние от заряда до точки поля, в которой определяется его напряженность. Заряды 61 и Ол отрицательны, следовательно, векторы его Ет и Е2 направлены по линиям напряженности к зарядам. По условию заряды Q\ — Q2 расположены на одинаковом расстоянии от точки Л, поэтому ЕХ=Е2. Следовательно, формула (2) принимает вид Е=2ЕХ • cos а, где cosa—h/r^
h=OA=^rl-rll4;
h=-J(5 ■ 10'2 м2)2—(4 ' IO"2 м)2 = 3 • 10'2 м.
Тогда напряженность в точке А
2Qi h
^=—
47Г££оГ^

=480 В/м.
2 9 1(Г9 Кл 3 10"2 м
4 3,14 81 8,85 10"12 Ф/м (0,05)3 м2
Потенциал ф, создаваемый системой точечных зарядов в данной точке поля, равен алгебраической сумме потенциалов, создава-
емых каждым из зарядов ср = £ (р±. Потенциал ср результирующе- 1"1 т-г
го поля в точке А равен (p = cpi + cp2- Потенциал поля, создава
емого точечным зарядом, ф=(2/(47гее0г). Следовательно,
Ci 0.2 201
= ,+ <р2=- ;
47Г££ог1 4Я££оГ2 4Я££оГ1
4 3,14 81 8,85 10’12 Ф/м 5 10'2
Ответ’. £=480 В/м; (р — — 40 В.
-
Заряд 1 нКл переносится в воздухе из точки, находящейся на расстоянии 1 м от бесконечно длинной равномерно заряженной нити, в точку на расстоянии 10 см от нее. Определить работу, совершаемую против сил поля, если линейная плотность заряда нити 1 мкКл/м. Какая работа совершается на последних 10 см пути?
Дано: го=О,1 м; п = 1 м; г2=0,2 м; Q=1 109 Кл; е=1; т= 1 • 10-6 Кл/м.
Найти: А2.
Решение. Работа внешней силы по перемещению заряда Q из точки поля с потенциалом (pt в точку с потенциалом <р0 равна
^ = С(фоФ1). О)
Бесконечная равномерно заряженная нить с линейной плотностью заряда т создает аксиально-симметричное поле напряженностью £=т/(27гее0г). Напряженность и потенциал этого поля d
связаны соотношением £= , откуда d
Edr. Разность
dr
потенциалов точек поля на расстоянии г, и г0 от нити
Г0


Фо-ф.= -
£dr =
т f dr т г*
-= In
2леео J г 2пеео го
г

И In
Го
i
Т
Фо-<Р1 = П
2Л6£о

(2)
Г2
(Р0-(Р2 = — Ь
2я££0 г0
Подставляя в формулу (1) найденное выражение для разности потенциалов из (2), определим работу, совершаемую внешними силами по перемещению заряда из точки, находящейся на расстоянии 1 м, до точки, расположенной на расстоянии 0,1 м от нити:
2л££о го’

• 10'J Дж.
, 1 • 10’9 Кл 1 • 1О’€ Кл/м In 10 , .
А1 = — =4,1
2 3,14 8,85 1012 Ф/м
„ 1 • 10"9 ■ 1 • 10€ In 10
Вычислим на калькуляторе выражение —■ по
2 3,14 8,85 10-12
программе
1[вп|9[7ч1И 1®б[Н10 югаа 2 0EI008,85R 1|вп] 12I/-/IR
Показания индикатора: 4,14087 10 5, т. е. 4,1 • 10“5 Дж.
Работа по перемещению заряда на последних 10 см пути равна
С т, Г2
Л2= In -;
2леео г0
, 1 • Ю 9 Кл 10 б Кл/м 1п2 , _ _ , „
Л2 = 7 - = 1,25 • 10'5 Дж.
2 3,14 8,85 10-12 Ф/м
Ответ: Л1 = 4,1 ' 10 5 Дж; Л2=1,25 • 10 5 Дж.
-
К одной из обкладок плоского конденсатора прилегает стеклянная плоскопараллельная пластинка (£1 = 7) толщиной 9 мм. После того как конденсатор отключили от источника напряжения 220 В и вынули стеклянную пластинку, между обкладками установилась разность потенциалов 976 В. Определить зазор между обкладками и отношение конечной и начальной энергии конденсатора.
Дано: С7!=220 В; (72=976 В; dj = 9 103 м; £1 = 7; е2=1.
Найти: do; W\/W2.
Решение. После отключения конденсатора и удаления стеклянной пластинки заряд на его обкладках остается неизменным, т. е. выполняется равенство
Cit7i = C2t/2, (1)
где С\ и С2 — электроемкости конденсатора в начальном и конечном случае.
По условию конденсатор вначале является слоистым и его электроемкость определяется по формуле
Eg ‘ S

(2)
G= —
di dodi
— +
£1 Е2
где 5 — площадь обкладок; d0 — зазор между ними, dx — толщина стеклянной пластинки, Ej и е2 — диэлектрические проницаемости стекла и воздуха соответственно.

E2£oS
После удаления стеклянной пластинки электроемкость конденсатора
(3)
Подставляя (2) и (3) в (1), получим
£о5С/1 £2£o5L/2
d\ do d\ dQ
£1 £2
откуда

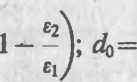






“о—
U2-Ui
976 В 9 IO-3
(976 - 220) В
м
1-’|=1 • 10’2 7/
M.
Начальная и конечная энергии конденсатора
CiU2. C2u22
W\=—; W2=—.
2 2
Тогда отношение этих энергий W2/Wi = C2U2/(CiUl). Учитывая (1), получим
W2 U2 W2 976 В . . .
——• — = 4 44
Wi Uif Wi 220 В
Ответ: do=l ' Ю“2 м; FF2/FFi=4,44.
-
Батарею из двух конденсаторов емкостью 400 и 500 пФ соединили последовательно и включили в сеть с напряжением 220 В. Потом батарею отключили от сети, конденсаторы разъединили и соединили параллельно обкладками, имеющими одноименные заряды. Каким будет напряжение на зажимах полученной батареи?
Дано: £7j = 220 В; Cj=400 пФ; С2=500 пФ.
Найти: U2.
Решение. У последовательно соединенных конденсаторов заряды на обкладках равны по модулю 61 = 62=6 и заряд батареи равен заряду одного конденсатора. Емкость батареи последовательно соединенных конденсаторов определяется по формуле п
1/С= £ 1/С«. Для батареи из двух конденсаторов
С=С, • С2/(С, + С2),
а их заряд
6 = СС/1 = С1С2С/1/(С1 + С2). (1)
При отключении конденсаторов их заряд сохраняется. У параллельно соединенных конденсаторов заряд батареи равен сумме зарядов конденсаторов 6=61 + 62» а емкость — сумме емкостей
С' = С\ + С2.
Напряжение на зажимах батареи из двух параллельно соединенных конденсаторов
Г 7 — R — _ 3^ /п\
2CCl + C2Cl-hC2' '
Подставляя (1) в (2), получаем
2CjC2?7i
(^1 + С2)
гт 2 4 5 • Ю-20 Ф2 • 220 В
tf2 = — - =108,6 В.
92 1О20 Ф2
Ответ'. t/2= 108,6 В.
-
Заряд конденсатора 1 мкКл, площадь пластин 100 см2, зазор между пластинками заполнен слюдой. Определить объемную плотность энергии поля конденсатора и силу притяжения пластин.
Дано: 6=Ю 6 Кл; 5= 10“2 м2; е=6.
Найти: >v; F.

(1)
Решение. Сила притяжения между двумя разноименно заряженными обкладками конденсатора уг .“о£2 5 ” 2
где Е — напряженность поля конденсатора; S — площадь обкладок конденсатора; е — диэлектрическая проницаемость слюды; Eq — электрическая постоянная.

(2)
Напряженность однородного поля плоского конденсатора _ ff Q Е==. ££q EEqS
где o=QIS — поверхностная плотность заряда. Подставляя (2) в (1), получаем
о2 Ю“12 Кл2
— = 0,94 Н. 2&£qS 2 6 8,85 10“12 Ф/м 10“2 м2
Объемная плотность энергии электрического поля

(3)
££qE2
W= — .
2
Подставляя (2) в (3), получаем
Q2 ю12 Кл2 -
w=——w=- —- = 94,2 Дж/м3.
2££0S2 2 • 6 8,85 10“12 Ф/м 10“* м4
Ответ: J’=0,94 Н; w=94,2 Дж/м.
-
В медном проводнике сечением 6 мм и длиной 5 м течет ток. За 1 мин в проводнике выделяется 18 Дж теплоты. Определить напряженность поля, плотность и силу электрического тока в проводнике.
Дано: 5=6 • 106 м2; 1=5 м; /=60 с; Q= 18 Дж; р = 1,7 • 10 8 Ом ■ м.
Найти: £; j; J.
Решение. Для решения задачи используем законы Ома и Джоуля — Ленца. Закон Ома в дифференциальной форме имеет вид
(о где j — плотность тока; Е — напряженность доля; у — удельная проводимость.
Закон Джоуля — Ленца
Q^Rt. (2)
Здесь J — сила тока, t — время,
R=p' (3)
д
— сопротивление проводника, где р, I, S — удельное сопротивление, длина и площадь поперечного сечения проводника соответственно.
Силу тока J находим из (2) с учетом (3):
т [q [qS I 18 Дж 6 10-6 м2
J= /—= / ; 7= -=4,6 A.
у Rt у pit у 1,7 10 8 Ом м 5 м 60 с
По определению, плотность тока равна j=J[S\
j=4,6 А/(6 • 10"6 м2) = 7,7 • 105 А/м2.
Напряженность поля в проводнике определим из (1), учитывая, что у=\1р.
E=j- р; Е=7,7 • 105 А/м2 • 1,7 КГ8 Ом • м=1,3 • 10'2 В/м.
Ответ: Е=1,3 10“2 В/м; J=4,6 A; 7=7,7 ■ 105 А/м2.
-
Внутреннее сопротивление аккумулятора 2 Ом. При замыкании его одним резистором сила тока равна 4 А, при замыкании другим — 2 А. Во внешней цепи в обоих случаях выделяется одинаковая мощность. Определить электродвижущую силу аккумулятора и внешние сопротивления.
Дано: г-2 Ом; 7] = 4 A; J2—2 A; NX=N2.
Найти: <5 ; 2^; R2-
Решение. Закон Ома для замкнутой (полной) цепи имеет вид

где г — внутреннее сопротивление источника тока; & — э. д. с. аккумулятора; R}iiR2 — внешние сопротивления цепей.
Уравнения (1) представим в виде
<5=Л(А, + г); 6=Л№+г). (2)
Из равенства> (2) следует, что
71(А1+г)=Л№+г). (3)
Мощность, выделяемая во внешней цепи в первом и втором случаях, соответственно равна
N2=JiR2.
Из условия равенства мощностей следует, что

Решая совместно уравнения (3) и (4), получаем

(4)
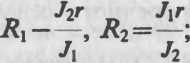

(5)
Л 2 А 2 Ом , _ Л 4 А • 2 Ом л _
— = 1 Ом, R2= = 4 Ом.
4 А 2 А
Подставляя (5) в (2), получаем
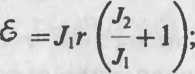 5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
Ответ: & = 12 В; Rt= 1 Ом; Л2 = 4 Ом.
-
Электродвижущая сила батареи равна 20 В. Коэффициент полезного действия батареи составляет 0,8 при силе тока 4 А. Чему равно внутреннее сопротивление батареи?
Дано: £ =20 В; >7 = 0,8; .7=4 А.
Найти: г.
Решение. Коэффициент полезного действия источника тока t] равен отношению падения напряжения во внешней цепи к его электродвижущей силе.
откуда
(2)
Используя выражение закона Ома для замкнутой цепи J= £/(Л+г), получаем
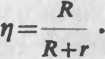
Подставляя (2) в (3) и выполняя преобразования, находим
ё(1-п) 20 в (1-0,8)
г= : г= =1 Ом.
Ответ: г— 1 Ом.
-
По двум бесконечно длинным прямолинейным проводникам, находящимся на расстоянии 50 см друг от друга, в одном направлении текут токи J\ и J2 силой по 5 А. Между проводниками на расстоянии 30 см от первого расположен кольцевой проводник с током J3 силой 5 А (рис. 3). Радиус кольца 20 см. Определить индукцию и напряженность магнитного поля, создаваемого токами в центре кольцевого проводника.
Дано: J1=J2=J3=J=5 А; ^=0,2 м; г3=0,2 м.
Найти: В\ Н.
Решение. В соответствии с принципом суперпозиции индукция результирующего магнитного поля в точке А равна
В = Bj 4-Вг + В3, (1)
где Bi и В2 — индукции полей, создаваемых соответственно токами Ji и J2, направленными за плоскость рисунка; Вз — индукция поля, создаваемая кольцевым током. Как видно из рис. 3, векторы В) и Bi направлены по одной прямой в противоположные стороны, поэтому их сумма В, 4-82 = 812 равна по модулю
В{2—В2 — Bi. (2)

(3)
Индукция поля, создаваемого бесконечно длинным проводником с током,

где До — магнитная постоянная; д — магнитная проницаемость
о\——; В2———,
2nr\ 2itr2
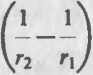





п л12=——
2л
5>
1 ... 4 5 6 7 8 9 10 11 12
E=Ej Ч-Ез.
По теореме косинусов
Е=у/Ё11+ё(+2Ё1 ' £? • cos 2а. (2)
Напряженность поля точечного заряда Q
E=QI(4nEE0r2)f
где е — диэлектрическая проницаемость; Ео — электрическая постоянная; г — расстояние от заряда до точки поля, в которой определяется его напряженность. Заряды 61 и Ол отрицательны, следовательно, векторы его Ет и Е2 направлены по линиям напряженности к зарядам. По условию заряды Q\ — Q2 расположены на одинаковом расстоянии от точки Л, поэтому ЕХ=Е2. Следовательно, формула (2) принимает вид Е=2ЕХ • cos а, где cosa—h/r^
h=OA=^rl-rll4;
h=-J(5 ■ 10'2 м2)2—(4 ' IO"2 м)2 = 3 • 10'2 м.
Тогда напряженность в точке А
2Qi h
^=—
47Г££оГ^

=480 В/м.
2 9 1(Г9 Кл 3 10"2 м
4 3,14 81 8,85 10"12 Ф/м (0,05)3 м2
Потенциал ф, создаваемый системой точечных зарядов в данной точке поля, равен алгебраической сумме потенциалов, создава-
емых каждым из зарядов ср = £ (р±. Потенциал ср результирующе- 1"1 т-г
го поля в точке А равен (p = cpi + cp2- Потенциал поля, создава
емого точечным зарядом, ф=(2/(47гее0г). Следовательно,
Ci 0.2 201
= ,+ <р2=- ;
47Г££ог1 4Я££оГ2 4Я££оГ1
4 3,14 81 8,85 10’12 Ф/м 5 10'2
Ответ’. £=480 В/м; (р — — 40 В.
-
Заряд 1 нКл переносится в воздухе из точки, находящейся на расстоянии 1 м от бесконечно длинной равномерно заряженной нити, в точку на расстоянии 10 см от нее. Определить работу, совершаемую против сил поля, если линейная плотность заряда нити 1 мкКл/м. Какая работа совершается на последних 10 см пути?
Дано: го=О,1 м; п = 1 м; г2=0,2 м; Q=1 109 Кл; е=1; т= 1 • 10-6 Кл/м.
Найти: А2.
Решение. Работа внешней силы по перемещению заряда Q из точки поля с потенциалом (pt в точку с потенциалом <р0 равна
^ = С(фоФ1). О)
Бесконечная равномерно заряженная нить с линейной плотностью заряда т создает аксиально-симметричное поле напряженностью £=т/(27гее0г). Напряженность и потенциал этого поля d
связаны соотношением £= , откуда d
Edr. Разность
dr
потенциалов точек поля на расстоянии г, и г0 от нити
Г0


Фо-ф.= -
£dr =
т f dr т г*
-= In
2леео J г 2пеео го
г

И In
Го
i
Т
Фо-<Р1 = П
2Л6£о

(2)
Г2
(Р0-(Р2 = — Ь
2я££0 г0
Подставляя в формулу (1) найденное выражение для разности потенциалов из (2), определим работу, совершаемую внешними силами по перемещению заряда из точки, находящейся на расстоянии 1 м, до точки, расположенной на расстоянии 0,1 м от нити:
2л££о го’

• 10'J Дж.
, 1 • 10’9 Кл 1 • 1О’€ Кл/м In 10 , .
А1 = — =4,1
2 3,14 8,85 1012 Ф/м
„ 1 • 10"9 ■ 1 • 10€ In 10
Вычислим на калькуляторе выражение —■ по
2 3,14 8,85 10-12
программе
1[вп|9[7ч1И 1®б[Н10 югаа 2 0EI008,85R 1|вп] 12I/-/IR
Показания индикатора: 4,14087 10 5, т. е. 4,1 • 10“5 Дж.
Работа по перемещению заряда на последних 10 см пути равна
С т, Г2
Л2= In -;
2леео г0
, 1 • Ю 9 Кл 10 б Кл/м 1п2 , _ _ , „
Л2 = 7 - = 1,25 • 10'5 Дж.
2 3,14 8,85 10-12 Ф/м
Ответ: Л1 = 4,1 ' 10 5 Дж; Л2=1,25 • 10 5 Дж.
-
К одной из обкладок плоского конденсатора прилегает стеклянная плоскопараллельная пластинка (£1 = 7) толщиной 9 мм. После того как конденсатор отключили от источника напряжения 220 В и вынули стеклянную пластинку, между обкладками установилась разность потенциалов 976 В. Определить зазор между обкладками и отношение конечной и начальной энергии конденсатора.
Дано: С7!=220 В; (72=976 В; dj = 9 103 м; £1 = 7; е2=1.
Найти: do; W\/W2.
Решение. После отключения конденсатора и удаления стеклянной пластинки заряд на его обкладках остается неизменным, т. е. выполняется равенство
Cit7i = C2t/2, (1)
где С\ и С2 — электроемкости конденсатора в начальном и конечном случае.
По условию конденсатор вначале является слоистым и его электроемкость определяется по формуле
Eg ‘ S

(2)
G= —
di dodi
— +
£1 Е2
где 5 — площадь обкладок; d0 — зазор между ними, dx — толщина стеклянной пластинки, Ej и е2 — диэлектрические проницаемости стекла и воздуха соответственно.

E2£oS
После удаления стеклянной пластинки электроемкость конденсатора
(3)
Подставляя (2) и (3) в (1), получим
£о5С/1 £2£o5L/2
d\ do d\ dQ
£1 £2
откуда

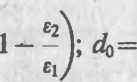






“о—
U2-Ui
976 В 9 IO-3
(976 - 220) В
м
1-’|=1 • 10’2 7/
M.
Начальная и конечная энергии конденсатора
CiU2. C2u22
W\=—; W2=—.
2 2
Тогда отношение этих энергий W2/Wi = C2U2/(CiUl). Учитывая (1), получим
W2 U2 W2 976 В . . .
——• — = 4 44
Wi Uif Wi 220 В
Ответ: do=l ' Ю“2 м; FF2/FFi=4,44.
-
Батарею из двух конденсаторов емкостью 400 и 500 пФ соединили последовательно и включили в сеть с напряжением 220 В. Потом батарею отключили от сети, конденсаторы разъединили и соединили параллельно обкладками, имеющими одноименные заряды. Каким будет напряжение на зажимах полученной батареи?
Дано: £7j = 220 В; Cj=400 пФ; С2=500 пФ.
Найти: U2.
Решение. У последовательно соединенных конденсаторов заряды на обкладках равны по модулю 61 = 62=6 и заряд батареи равен заряду одного конденсатора. Емкость батареи последовательно соединенных конденсаторов определяется по формуле п
1/С= £ 1/С«. Для батареи из двух конденсаторов
С=С, • С2/(С, + С2),
а их заряд
6 = СС/1 = С1С2С/1/(С1 + С2). (1)
При отключении конденсаторов их заряд сохраняется. У параллельно соединенных конденсаторов заряд батареи равен сумме зарядов конденсаторов 6=61 + 62» а емкость — сумме емкостей
С' = С\ + С2.
Напряжение на зажимах батареи из двух параллельно соединенных конденсаторов
Г 7 — R — _ 3^ /п\
2CCl + C2Cl-hC2' '
Подставляя (1) в (2), получаем
2CjC2?7i
(^1 + С2)
гт 2 4 5 • Ю-20 Ф2 • 220 В
tf2 = — - =108,6 В.
92 1О20 Ф2
Ответ'. t/2= 108,6 В.
-
Заряд конденсатора 1 мкКл, площадь пластин 100 см2, зазор между пластинками заполнен слюдой. Определить объемную плотность энергии поля конденсатора и силу притяжения пластин.
Дано: 6=Ю 6 Кл; 5= 10“2 м2; е=6.
Найти: >v; F.

(1)
Решение. Сила притяжения между двумя разноименно заряженными обкладками конденсатора уг .“о£2 5 ” 2
где Е — напряженность поля конденсатора; S — площадь обкладок конденсатора; е — диэлектрическая проницаемость слюды; Eq — электрическая постоянная.

(2)
Напряженность однородного поля плоского конденсатора _ ff Q Е==. ££q EEqS
где o=QIS — поверхностная плотность заряда. Подставляя (2) в (1), получаем
о2 Ю“12 Кл2
— = 0,94 Н. 2&£qS 2 6 8,85 10“12 Ф/м 10“2 м2
Объемная плотность энергии электрического поля

(3)
££qE2
W= — .
2
Подставляя (2) в (3), получаем
Q2 ю12 Кл2 -
w=——w=- —- = 94,2 Дж/м3.
2££0S2 2 • 6 8,85 10“12 Ф/м 10“* м4
Ответ: J’=0,94 Н; w=94,2 Дж/м.
-
В медном проводнике сечением 6 мм и длиной 5 м течет ток. За 1 мин в проводнике выделяется 18 Дж теплоты. Определить напряженность поля, плотность и силу электрического тока в проводнике.
Дано: 5=6 • 106 м2; 1=5 м; /=60 с; Q= 18 Дж; р = 1,7 • 10 8 Ом ■ м.
Найти: £; j; J.
Решение. Для решения задачи используем законы Ома и Джоуля — Ленца. Закон Ома в дифференциальной форме имеет вид
(о где j — плотность тока; Е — напряженность доля; у — удельная проводимость.
Закон Джоуля — Ленца
Q^Rt. (2)
Здесь J — сила тока, t — время,
R=p' (3)
д
— сопротивление проводника, где р, I, S — удельное сопротивление, длина и площадь поперечного сечения проводника соответственно.
Силу тока J находим из (2) с учетом (3):
т [q [qS I 18 Дж 6 10-6 м2
J= /—= / ; 7= -=4,6 A.
у Rt у pit у 1,7 10 8 Ом м 5 м 60 с
По определению, плотность тока равна j=J[S\
j=4,6 А/(6 • 10"6 м2) = 7,7 • 105 А/м2.
Напряженность поля в проводнике определим из (1), учитывая, что у=\1р.
E=j- р; Е=7,7 • 105 А/м2 • 1,7 КГ8 Ом • м=1,3 • 10'2 В/м.
Ответ: Е=1,3 10“2 В/м; J=4,6 A; 7=7,7 ■ 105 А/м2.
-
Внутреннее сопротивление аккумулятора 2 Ом. При замыкании его одним резистором сила тока равна 4 А, при замыкании другим — 2 А. Во внешней цепи в обоих случаях выделяется одинаковая мощность. Определить электродвижущую силу аккумулятора и внешние сопротивления.
Дано: г-2 Ом; 7] = 4 A; J2—2 A; NX=N2.
Найти: <5 ; 2^; R2-
Решение. Закон Ома для замкнутой (полной) цепи имеет вид

где г — внутреннее сопротивление источника тока; & — э. д. с. аккумулятора; R}iiR2 — внешние сопротивления цепей.
Уравнения (1) представим в виде
<5=Л(А, + г); 6=Л№+г). (2)
Из равенства> (2) следует, что
71(А1+г)=Л№+г). (3)
Мощность, выделяемая во внешней цепи в первом и втором случаях, соответственно равна
N2=JiR2.
Из условия равенства мощностей следует, что

Решая совместно уравнения (3) и (4), получаем

(4)
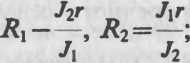

(5)
Л 2 А 2 Ом , _ Л 4 А • 2 Ом л _
— = 1 Ом, R2= = 4 Ом.
4 А 2 А
Подставляя (5) в (2), получаем
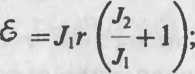 5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
Ответ: & = 12 В; Rt= 1 Ом; Л2 = 4 Ом.
-
Электродвижущая сила батареи равна 20 В. Коэффициент полезного действия батареи составляет 0,8 при силе тока 4 А. Чему равно внутреннее сопротивление батареи?
Дано: £ =20 В; >7 = 0,8; .7=4 А.
Найти: г.
Решение. Коэффициент полезного действия источника тока t] равен отношению падения напряжения во внешней цепи к его электродвижущей силе.
откуда
(2)
Используя выражение закона Ома для замкнутой цепи J= £/(Л+г), получаем
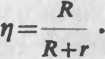
Подставляя (2) в (3) и выполняя преобразования, находим
ё(1-п) 20 в (1-0,8)
г= : г= =1 Ом.
Ответ: г— 1 Ом.
-
По двум бесконечно длинным прямолинейным проводникам, находящимся на расстоянии 50 см друг от друга, в одном направлении текут токи J\ и J2 силой по 5 А. Между проводниками на расстоянии 30 см от первого расположен кольцевой проводник с током J3 силой 5 А (рис. 3). Радиус кольца 20 см. Определить индукцию и напряженность магнитного поля, создаваемого токами в центре кольцевого проводника.
Дано: J1=J2=J3=J=5 А; ^=0,2 м; г3=0,2 м.
Найти: В\ Н.
Решение. В соответствии с принципом суперпозиции индукция результирующего магнитного поля в точке А равна
В = Bj 4-Вг + В3, (1)
где Bi и В2 — индукции полей, создаваемых соответственно токами Ji и J2, направленными за плоскость рисунка; Вз — индукция поля, создаваемая кольцевым током. Как видно из рис. 3, векторы В) и Bi направлены по одной прямой в противоположные стороны, поэтому их сумма В, 4-82 = 812 равна по модулю
В{2—В2 — Bi. (2)

(3)
Индукция поля, создаваемого бесконечно длинным проводником с током,

где До — магнитная постоянная; д — магнитная проницаемость
о\——; В2———,
2nr\ 2itr2
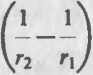





п л12=——
2л
5>
1 ... 4 5 6 7 8 9 10 11 12
E=Ej Ч-Ез.
По теореме косинусов
Е=у/Ё11+ё(+2Ё1 ' £? • cos 2а. (2)
Напряженность поля точечного заряда Q
E=QI(4nEE0r2)f
где е — диэлектрическая проницаемость; Ео — электрическая постоянная; г — расстояние от заряда до точки поля, в которой определяется его напряженность. Заряды 61 и Ол отрицательны, следовательно, векторы его Ет и Е2 направлены по линиям напряженности к зарядам. По условию заряды Q\ — Q2 расположены на одинаковом расстоянии от точки Л, поэтому ЕХ=Е2. Следовательно, формула (2) принимает вид Е=2ЕХ • cos а, где cosa—h/r^
h=OA=^rl-rll4;
h=-J(5 ■ 10'2 м2)2—(4 ' IO"2 м)2 = 3 • 10'2 м.
Тогда напряженность в точке А
2Qi h
^=—
47Г££оГ^

=480 В/м.
2 9 1(Г9 Кл 3 10"2 м
4 3,14 81 8,85 10"12 Ф/м (0,05)3 м2
Потенциал ф, создаваемый системой точечных зарядов в данной точке поля, равен алгебраической сумме потенциалов, создава-
емых каждым из зарядов ср = £ (р±. Потенциал ср результирующе- 1"1 т-г
го поля в точке А равен (p = cpi + cp2- Потенциал поля, создава
емого точечным зарядом, ф=(2/(47гее0г). Следовательно,
Ci 0.2 201
= ,+ <р2=- ;
47Г££ог1 4Я££оГ2 4Я££оГ1
4 3,14 81 8,85 10’12 Ф/м 5 10'2
Ответ’. £=480 В/м; (р — — 40 В.
-
Заряд 1 нКл переносится в воздухе из точки, находящейся на расстоянии 1 м от бесконечно длинной равномерно заряженной нити, в точку на расстоянии 10 см от нее. Определить работу, совершаемую против сил поля, если линейная плотность заряда нити 1 мкКл/м. Какая работа совершается на последних 10 см пути?
Дано: го=О,1 м; п = 1 м; г2=0,2 м; Q=1 109 Кл; е=1; т= 1 • 10-6 Кл/м.
Найти: А2.
Решение. Работа внешней силы по перемещению заряда Q из точки поля с потенциалом (pt в точку с потенциалом <р0 равна
^ = С(фоФ1). О)
Бесконечная равномерно заряженная нить с линейной плотностью заряда т создает аксиально-симметричное поле напряженностью £=т/(27гее0г). Напряженность и потенциал этого поля d
связаны соотношением £= , откуда d
Edr. Разность
dr
потенциалов точек поля на расстоянии г, и г0 от нити
Г0


Фо-ф.= -
£dr =
т f dr т г*
-= In
2леео J г 2пеео го
г

И In
Го
i
Т
Фо-<Р1 = П
2Л6£о

(2)
Г2
(Р0-(Р2 = — Ь
2я££0 г0
Подставляя в формулу (1) найденное выражение для разности потенциалов из (2), определим работу, совершаемую внешними силами по перемещению заряда из точки, находящейся на расстоянии 1 м, до точки, расположенной на расстоянии 0,1 м от нити:
2л££о го’

• 10'J Дж.
, 1 • 10’9 Кл 1 • 1О’€ Кл/м In 10 , .
А1 = — =4,1
2 3,14 8,85 1012 Ф/м
„ 1 • 10"9 ■ 1 • 10€ In 10
Вычислим на калькуляторе выражение —■ по
2 3,14 8,85 10-12
программе
1[вп|9[7ч1И 1®б[Н10 югаа 2 0EI008,85R 1|вп] 12I/-/IR
Показания индикатора: 4,14087 10 5, т. е. 4,1 • 10“5 Дж.
Работа по перемещению заряда на последних 10 см пути равна
С т, Г2
Л2= In -;
2леео г0
, 1 • Ю 9 Кл 10 б Кл/м 1п2 , _ _ , „
Л2 = 7 - = 1,25 • 10'5 Дж.
2 3,14 8,85 10-12 Ф/м
Ответ: Л1 = 4,1 ' 10 5 Дж; Л2=1,25 • 10 5 Дж.
-
К одной из обкладок плоского конденсатора прилегает стеклянная плоскопараллельная пластинка (£1 = 7) толщиной 9 мм. После того как конденсатор отключили от источника напряжения 220 В и вынули стеклянную пластинку, между обкладками установилась разность потенциалов 976 В. Определить зазор между обкладками и отношение конечной и начальной энергии конденсатора.
Дано: С7!=220 В; (72=976 В; dj = 9 103 м; £1 = 7; е2=1.
Найти: do; W\/W2.
Решение. После отключения конденсатора и удаления стеклянной пластинки заряд на его обкладках остается неизменным, т. е. выполняется равенство
Cit7i = C2t/2, (1)
где С\ и С2 — электроемкости конденсатора в начальном и конечном случае.
По условию конденсатор вначале является слоистым и его электроемкость определяется по формуле
Eg ‘ S

(2)
G= —
di dodi
— +
£1 Е2
где 5 — площадь обкладок; d0 — зазор между ними, dx — толщина стеклянной пластинки, Ej и е2 — диэлектрические проницаемости стекла и воздуха соответственно.

E2£oS
После удаления стеклянной пластинки электроемкость конденсатора
(3)
Подставляя (2) и (3) в (1), получим
£о5С/1 £2£o5L/2
d\ do d\ dQ
£1 £2
откуда

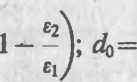






“о—
U2-Ui
976 В 9 IO-3
(976 - 220) В
м
1-’|=1 • 10’2 7/
M.
Начальная и конечная энергии конденсатора
CiU2. C2u22
W\=—; W2=—.
2 2
Тогда отношение этих энергий W2/Wi = C2U2/(CiUl). Учитывая (1), получим
W2 U2 W2 976 В . . .
——• — = 4 44
Wi Uif Wi 220 В
Ответ: do=l ' Ю“2 м; FF2/FFi=4,44.
-
Батарею из двух конденсаторов емкостью 400 и 500 пФ соединили последовательно и включили в сеть с напряжением 220 В. Потом батарею отключили от сети, конденсаторы разъединили и соединили параллельно обкладками, имеющими одноименные заряды. Каким будет напряжение на зажимах полученной батареи?
Дано: £7j = 220 В; Cj=400 пФ; С2=500 пФ.
Найти: U2.
Решение. У последовательно соединенных конденсаторов заряды на обкладках равны по модулю 61 = 62=6 и заряд батареи равен заряду одного конденсатора. Емкость батареи последовательно соединенных конденсаторов определяется по формуле п
1/С= £ 1/С«. Для батареи из двух конденсаторов
С=С, • С2/(С, + С2),
а их заряд
6 = СС/1 = С1С2С/1/(С1 + С2). (1)
При отключении конденсаторов их заряд сохраняется. У параллельно соединенных конденсаторов заряд батареи равен сумме зарядов конденсаторов 6=61 + 62» а емкость — сумме емкостей
С' = С\ + С2.
Напряжение на зажимах батареи из двух параллельно соединенных конденсаторов
Г 7 — R — _ 3^ /п\
2CCl + C2Cl-hC2' '
Подставляя (1) в (2), получаем
2CjC2?7i
(^1 + С2)
гт 2 4 5 • Ю-20 Ф2 • 220 В
tf2 = — - =108,6 В.
92 1О20 Ф2
Ответ'. t/2= 108,6 В.
-
Заряд конденсатора 1 мкКл, площадь пластин 100 см2, зазор между пластинками заполнен слюдой. Определить объемную плотность энергии поля конденсатора и силу притяжения пластин.
Дано: 6=Ю 6 Кл; 5= 10“2 м2; е=6.
Найти: >v; F.

(1)
Решение. Сила притяжения между двумя разноименно заряженными обкладками конденсатора уг .“о£2 5 ” 2
где Е — напряженность поля конденсатора; S — площадь обкладок конденсатора; е — диэлектрическая проницаемость слюды; Eq — электрическая постоянная.

(2)
Напряженность однородного поля плоского конденсатора _ ff Q Е==. ££q EEqS
где o=QIS — поверхностная плотность заряда. Подставляя (2) в (1), получаем
о2 Ю“12 Кл2
— = 0,94 Н. 2&£qS 2 6 8,85 10“12 Ф/м 10“2 м2
Объемная плотность энергии электрического поля

(3)
££qE2
W= — .
2
Подставляя (2) в (3), получаем
Q2 ю12 Кл2 -
w=——w=- —- = 94,2 Дж/м3.
2££0S2 2 • 6 8,85 10“12 Ф/м 10“* м4
Ответ: J’=0,94 Н; w=94,2 Дж/м.
-
В медном проводнике сечением 6 мм и длиной 5 м течет ток. За 1 мин в проводнике выделяется 18 Дж теплоты. Определить напряженность поля, плотность и силу электрического тока в проводнике.
Дано: 5=6 • 106 м2; 1=5 м; /=60 с; Q= 18 Дж; р = 1,7 • 10 8 Ом ■ м.
Найти: £; j; J.
Решение. Для решения задачи используем законы Ома и Джоуля — Ленца. Закон Ома в дифференциальной форме имеет вид
(о где j — плотность тока; Е — напряженность доля; у — удельная проводимость.
Закон Джоуля — Ленца
Q^Rt. (2)
Здесь J — сила тока, t — время,
R=p' (3)
д
— сопротивление проводника, где р, I, S — удельное сопротивление, длина и площадь поперечного сечения проводника соответственно.
Силу тока J находим из (2) с учетом (3):
т [q [qS I 18 Дж 6 10-6 м2
J= /—= / ; 7= -=4,6 A.
у Rt у pit у 1,7 10 8 Ом м 5 м 60 с
По определению, плотность тока равна j=J[S\
j=4,6 А/(6 • 10"6 м2) = 7,7 • 105 А/м2.
Напряженность поля в проводнике определим из (1), учитывая, что у=\1р.
E=j- р; Е=7,7 • 105 А/м2 • 1,7 КГ8 Ом • м=1,3 • 10'2 В/м.
Ответ: Е=1,3 10“2 В/м; J=4,6 A; 7=7,7 ■ 105 А/м2.
-
Внутреннее сопротивление аккумулятора 2 Ом. При замыкании его одним резистором сила тока равна 4 А, при замыкании другим — 2 А. Во внешней цепи в обоих случаях выделяется одинаковая мощность. Определить электродвижущую силу аккумулятора и внешние сопротивления.
Дано: г-2 Ом; 7] = 4 A; J2—2 A; NX=N2.
Найти: <5 ; 2^; R2-
Решение. Закон Ома для замкнутой (полной) цепи имеет вид

где г — внутреннее сопротивление источника тока; & — э. д. с. аккумулятора; R}iiR2 — внешние сопротивления цепей.
Уравнения (1) представим в виде
<5=Л(А, + г); 6=Л№+г). (2)
Из равенства> (2) следует, что
71(А1+г)=Л№+г). (3)
Мощность, выделяемая во внешней цепи в первом и втором случаях, соответственно равна
N2=JiR2.
Из условия равенства мощностей следует, что

Решая совместно уравнения (3) и (4), получаем

(4)
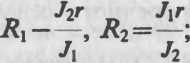

(5)
Л 2 А 2 Ом , _ Л 4 А • 2 Ом л _
— = 1 Ом, R2= = 4 Ом.
4 А 2 А
Подставляя (5) в (2), получаем
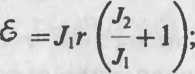 5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
Ответ: & = 12 В; Rt= 1 Ом; Л2 = 4 Ом.
-
Электродвижущая сила батареи равна 20 В. Коэффициент полезного действия батареи составляет 0,8 при силе тока 4 А. Чему равно внутреннее сопротивление батареи?
Дано: £ =20 В; >7 = 0,8; .7=4 А.
Найти: г.
Решение. Коэффициент полезного действия источника тока t] равен отношению падения напряжения во внешней цепи к его электродвижущей силе.
откуда
(2)
Используя выражение закона Ома для замкнутой цепи J= £/(Л+г), получаем
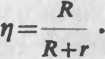
Подставляя (2) в (3) и выполняя преобразования, находим
ё(1-п) 20 в (1-0,8)
г= : г= =1 Ом.
Ответ: г— 1 Ом.
-
По двум бесконечно длинным прямолинейным проводникам, находящимся на расстоянии 50 см друг от друга, в одном направлении текут токи J\ и J2 силой по 5 А. Между проводниками на расстоянии 30 см от первого расположен кольцевой проводник с током J3 силой 5 А (рис. 3). Радиус кольца 20 см. Определить индукцию и напряженность магнитного поля, создаваемого токами в центре кольцевого проводника.
Дано: J1=J2=J3=J=5 А; ^=0,2 м; г3=0,2 м.
Найти: В\ Н.
Решение. В соответствии с принципом суперпозиции индукция результирующего магнитного поля в точке А равна
В = Bj 4-Вг + В3, (1)
где Bi и В2 — индукции полей, создаваемых соответственно токами Ji и J2, направленными за плоскость рисунка; Вз — индукция поля, создаваемая кольцевым током. Как видно из рис. 3, векторы В) и Bi направлены по одной прямой в противоположные стороны, поэтому их сумма В, 4-82 = 812 равна по модулю
В{2—В2 — Bi. (2)

(3)
Индукция поля, создаваемого бесконечно длинным проводником с током,

где До — магнитная постоянная; д — магнитная проницаемость
о\——; В2———,
2nr\ 2itr2
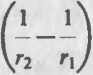





п л12=——
2л
5>
1 ... 4 5 6 7 8 9 10 11 12
E=Ej Ч-Ез.
По теореме косинусов
Е=у/Ё11+ё(+2Ё1 ' £? • cos 2а. (2)
Напряженность поля точечного заряда Q
E=QI(4nEE0r2)f
где е — диэлектрическая проницаемость; Ео — электрическая постоянная; г — расстояние от заряда до точки поля, в которой определяется его напряженность. Заряды 61 и Ол отрицательны, следовательно, векторы его Ет и Е2 направлены по линиям напряженности к зарядам. По условию заряды Q\ — Q2 расположены на одинаковом расстоянии от точки Л, поэтому ЕХ=Е2. Следовательно, формула (2) принимает вид Е=2ЕХ • cos а, где cosa—h/r^
h=OA=^rl-rll4;
h=-J(5 ■ 10'2 м2)2—(4 ' IO"2 м)2 = 3 • 10'2 м.
Тогда напряженность в точке А
2Qi h
^=—
47Г££оГ^

=480 В/м.
2 9 1(Г9 Кл 3 10"2 м
4 3,14 81 8,85 10"12 Ф/м (0,05)3 м2
Потенциал ф, создаваемый системой точечных зарядов в данной точке поля, равен алгебраической сумме потенциалов, создава-
емых каждым из зарядов ср = £ (р±. Потенциал ср результирующе- 1"1 т-г
го поля в точке А равен (p = cpi + cp2- Потенциал поля, создава
емого точечным зарядом, ф=(2/(47гее0г). Следовательно,
Ci 0.2 201
= ,+ <р2=- ;
47Г££ог1 4Я££оГ2 4Я££оГ1
4 3,14 81 8,85 10’12 Ф/м 5 10'2
Ответ’. £=480 В/м; (р — — 40 В.
-
Заряд 1 нКл переносится в воздухе из точки, находящейся на расстоянии 1 м от бесконечно длинной равномерно заряженной нити, в точку на расстоянии 10 см от нее. Определить работу, совершаемую против сил поля, если линейная плотность заряда нити 1 мкКл/м. Какая работа совершается на последних 10 см пути?
Дано: го=О,1 м; п = 1 м; г2=0,2 м; Q=1 109 Кл; е=1; т= 1 • 10-6 Кл/м.
Найти: А2.
Решение. Работа внешней силы по перемещению заряда Q из точки поля с потенциалом (pt в точку с потенциалом <р0 равна
^ = С(фоФ1). О)
Бесконечная равномерно заряженная нить с линейной плотностью заряда т создает аксиально-симметричное поле напряженностью £=т/(27гее0г). Напряженность и потенциал этого поля d
связаны соотношением £= , откуда d
Edr. Разность
dr
потенциалов точек поля на расстоянии г, и г0 от нити
Г0


Фо-ф.= -
£dr =
т f dr т г*
-= In
2леео J г 2пеео го
г

И In
Го
i
Т
Фо-<Р1 = П
2Л6£о

(2)
Г2
(Р0-(Р2 = — Ь
2я££0 г0
Подставляя в формулу (1) найденное выражение для разности потенциалов из (2), определим работу, совершаемую внешними силами по перемещению заряда из точки, находящейся на расстоянии 1 м, до точки, расположенной на расстоянии 0,1 м от нити:
2л££о го’

• 10'J Дж.
, 1 • 10’9 Кл 1 • 1О’€ Кл/м In 10 , .
А1 = — =4,1
2 3,14 8,85 1012 Ф/м
„ 1 • 10"9 ■ 1 • 10€ In 10
Вычислим на калькуляторе выражение —■ по
2 3,14 8,85 10-12
программе
1[вп|9[7ч1И 1®б[Н10 югаа 2 0EI008,85R 1|вп] 12I/-/IR
Показания индикатора: 4,14087 10 5, т. е. 4,1 • 10“5 Дж.
Работа по перемещению заряда на последних 10 см пути равна
С т, Г2
Л2= In -;
2леео г0
, 1 • Ю 9 Кл 10 б Кл/м 1п2 , _ _ , „
Л2 = 7 - = 1,25 • 10'5 Дж.
2 3,14 8,85 10-12 Ф/м
Ответ: Л1 = 4,1 ' 10 5 Дж; Л2=1,25 • 10 5 Дж.
-
К одной из обкладок плоского конденсатора прилегает стеклянная плоскопараллельная пластинка (£1 = 7) толщиной 9 мм. После того как конденсатор отключили от источника напряжения 220 В и вынули стеклянную пластинку, между обкладками установилась разность потенциалов 976 В. Определить зазор между обкладками и отношение конечной и начальной энергии конденсатора.
Дано: С7!=220 В; (72=976 В; dj = 9 103 м; £1 = 7; е2=1.
Найти: do; W\/W2.
Решение. После отключения конденсатора и удаления стеклянной пластинки заряд на его обкладках остается неизменным, т. е. выполняется равенство
Cit7i = C2t/2, (1)
где С\ и С2 — электроемкости конденсатора в начальном и конечном случае.
По условию конденсатор вначале является слоистым и его электроемкость определяется по формуле
Eg ‘ S

(2)
G= —
di dodi
— +
£1 Е2
где 5 — площадь обкладок; d0 — зазор между ними, dx — толщина стеклянной пластинки, Ej и е2 — диэлектрические проницаемости стекла и воздуха соответственно.

E2£oS
После удаления стеклянной пластинки электроемкость конденсатора
(3)
Подставляя (2) и (3) в (1), получим
£о5С/1 £2£o5L/2
d\ do d\ dQ
£1 £2
откуда

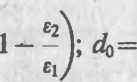






“о—
U2-Ui
976 В 9 IO-3
(976 - 220) В
м
1-’|=1 • 10’2 7/
M.
Начальная и конечная энергии конденсатора
CiU2. C2u22
W\=—; W2=—.
2 2
Тогда отношение этих энергий W2/Wi = C2U2/(CiUl). Учитывая (1), получим
W2 U2 W2 976 В . . .
——• — = 4 44
Wi Uif Wi 220 В
Ответ: do=l ' Ю“2 м; FF2/FFi=4,44.
-
Батарею из двух конденсаторов емкостью 400 и 500 пФ соединили последовательно и включили в сеть с напряжением 220 В. Потом батарею отключили от сети, конденсаторы разъединили и соединили параллельно обкладками, имеющими одноименные заряды. Каким будет напряжение на зажимах полученной батареи?
Дано: £7j = 220 В; Cj=400 пФ; С2=500 пФ.
Найти: U2.
Решение. У последовательно соединенных конденсаторов заряды на обкладках равны по модулю 61 = 62=6 и заряд батареи равен заряду одного конденсатора. Емкость батареи последовательно соединенных конденсаторов определяется по формуле п
1/С= £ 1/С«. Для батареи из двух конденсаторов
С=С, • С2/(С, + С2),
а их заряд
6 = СС/1 = С1С2С/1/(С1 + С2). (1)
При отключении конденсаторов их заряд сохраняется. У параллельно соединенных конденсаторов заряд батареи равен сумме зарядов конденсаторов 6=61 + 62» а емкость — сумме емкостей
С' = С\ + С2.
Напряжение на зажимах батареи из двух параллельно соединенных конденсаторов
Г 7 — R — _ 3^ /п\
2CCl + C2Cl-hC2' '
Подставляя (1) в (2), получаем
2CjC2?7i
(^1 + С2)
гт 2 4 5 • Ю-20 Ф2 • 220 В
tf2 = — - =108,6 В.
92 1О20 Ф2
Ответ'. t/2= 108,6 В.
-
Заряд конденсатора 1 мкКл, площадь пластин 100 см2, зазор между пластинками заполнен слюдой. Определить объемную плотность энергии поля конденсатора и силу притяжения пластин.
Дано: 6=Ю 6 Кл; 5= 10“2 м2; е=6.
Найти: >v; F.

(1)
Решение. Сила притяжения между двумя разноименно заряженными обкладками конденсатора уг .“о£2 5 ” 2
где Е — напряженность поля конденсатора; S — площадь обкладок конденсатора; е — диэлектрическая проницаемость слюды; Eq — электрическая постоянная.

(2)
Напряженность однородного поля плоского конденсатора _ ff Q Е==. ££q EEqS
где o=QIS — поверхностная плотность заряда. Подставляя (2) в (1), получаем
о2 Ю“12 Кл2
— = 0,94 Н. 2&£qS 2 6 8,85 10“12 Ф/м 10“2 м2
Объемная плотность энергии электрического поля

(3)
££qE2
W= — .
2
Подставляя (2) в (3), получаем
Q2 ю12 Кл2 -
w=——w=- —- = 94,2 Дж/м3.
2££0S2 2 • 6 8,85 10“12 Ф/м 10“* м4
Ответ: J’=0,94 Н; w=94,2 Дж/м.
-
В медном проводнике сечением 6 мм и длиной 5 м течет ток. За 1 мин в проводнике выделяется 18 Дж теплоты. Определить напряженность поля, плотность и силу электрического тока в проводнике.
Дано: 5=6 • 106 м2; 1=5 м; /=60 с; Q= 18 Дж; р = 1,7 • 10 8 Ом ■ м.
Найти: £; j; J.
Решение. Для решения задачи используем законы Ома и Джоуля — Ленца. Закон Ома в дифференциальной форме имеет вид
(о где j — плотность тока; Е — напряженность доля; у — удельная проводимость.
Закон Джоуля — Ленца
Q^Rt. (2)
Здесь J — сила тока, t — время,
R=p' (3)
д
— сопротивление проводника, где р, I, S — удельное сопротивление, длина и площадь поперечного сечения проводника соответственно.
Силу тока J находим из (2) с учетом (3):
т [q [qS I 18 Дж 6 10-6 м2
J= /—= / ; 7= -=4,6 A.
у Rt у pit у 1,7 10 8 Ом м 5 м 60 с
По определению, плотность тока равна j=J[S\
j=4,6 А/(6 • 10"6 м2) = 7,7 • 105 А/м2.
Напряженность поля в проводнике определим из (1), учитывая, что у=\1р.
E=j- р; Е=7,7 • 105 А/м2 • 1,7 КГ8 Ом • м=1,3 • 10'2 В/м.
Ответ: Е=1,3 10“2 В/м; J=4,6 A; 7=7,7 ■ 105 А/м2.
-
Внутреннее сопротивление аккумулятора 2 Ом. При замыкании его одним резистором сила тока равна 4 А, при замыкании другим — 2 А. Во внешней цепи в обоих случаях выделяется одинаковая мощность. Определить электродвижущую силу аккумулятора и внешние сопротивления.
Дано: г-2 Ом; 7] = 4 A; J2—2 A; NX=N2.
Найти: <5 ; 2^; R2-
Решение. Закон Ома для замкнутой (полной) цепи имеет вид

где г — внутреннее сопротивление источника тока; & — э. д. с. аккумулятора; R}iiR2 — внешние сопротивления цепей.
Уравнения (1) представим в виде
<5=Л(А, + г); 6=Л№+г). (2)
Из равенства> (2) следует, что
71(А1+г)=Л№+г). (3)
Мощность, выделяемая во внешней цепи в первом и втором случаях, соответственно равна
N2=JiR2.
Из условия равенства мощностей следует, что

Решая совместно уравнения (3) и (4), получаем

(4)
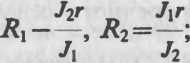

(5)
Л 2 А 2 Ом , _ Л 4 А • 2 Ом л _
— = 1 Ом, R2= = 4 Ом.
4 А 2 А
Подставляя (5) в (2), получаем
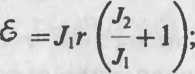 5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
5 = 4 А • 2 Ом(2 А/(4 А)+1)= 12 В.
Ответ: & = 12 В; Rt= 1 Ом; Л2 = 4 Ом.
-
Электродвижущая сила батареи равна 20 В. Коэффициент полезного действия батареи составляет 0,8 при силе тока 4 А. Чему равно внутреннее сопротивление батареи?
Дано: £ =20 В; >7 = 0,8; .7=4 А.
Найти: г.
Решение. Коэффициент полезного действия источника тока t] равен отношению падения напряжения во внешней цепи к его электродвижущей силе.
откуда
(2)
Используя выражение закона Ома для замкнутой цепи J= £/(Л+г), получаем
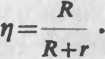
Подставляя (2) в (3) и выполняя преобразования, находим
ё(1-п) 20 в (1-0,8)
г= : г= =1 Ом.
Ответ: г— 1 Ом.
-
По двум бесконечно длинным прямолинейным проводникам, находящимся на расстоянии 50 см друг от друга, в одном направлении текут токи J\ и J2 силой по 5 А. Между проводниками на расстоянии 30 см от первого расположен кольцевой проводник с током J3 силой 5 А (рис. 3). Радиус кольца 20 см. Определить индукцию и напряженность магнитного поля, создаваемого токами в центре кольцевого проводника.
Дано: J1=J2=J3=J=5 А; ^=0,2 м; г3=0,2 м.
Найти: В\ Н.
Решение. В соответствии с принципом суперпозиции индукция результирующего магнитного поля в точке А равна
В = Bj 4-Вг + В3, (1)
где Bi и В2 — индукции полей, создаваемых соответственно токами Ji и J2, направленными за плоскость рисунка; Вз — индукция поля, создаваемая кольцевым током. Как видно из рис. 3, векторы В) и Bi направлены по одной прямой в противоположные стороны, поэтому их сумма В, 4-82 = 812 равна по модулю
В{2—В2 — Bi. (2)

(3)
Индукция поля, создаваемого бесконечно длинным проводником с током,

где До — магнитная постоянная; д — магнитная проницаемость
о\——; В2———,
2nr\ 2itr2
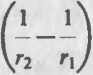





п л12=——
2л
5>
1 ... 4 5 6 7 8 9 10 11 12
емых каждым из зарядов ср = £ (р±. Потенциал ср результирующе- 1"1 т-г
го поля в точке А равен (p = cpi + cp2- Потенциал поля, создава
емого точечным зарядом, ф=(2/(47гее0г). Следовательно,
Ci 0.2 201
= ,+ <р2=- ;
47Г££ог1 4Я££оГ2 4Я££оГ1
4 3,14 81 8,85 10’12 Ф/м 5 10'2
Ответ’. £=480 В/м; (р — — 40 В.
-
Заряд 1 нКл переносится в воздухе из точки, находящейся на расстоянии 1 м от бесконечно длинной равномерно заряженной нити, в точку на расстоянии 10 см от нее. Определить работу, совершаемую против сил поля, если линейная плотность заряда нити 1 мкКл/м. Какая работа совершается на последних 10 см пути?
Дано: го=О,1 м; п = 1 м; г2=0,2 м; Q=1 109 Кл; е=1; т= 1 • 10-6 Кл/м.
Найти: А2.
Решение. Работа внешней силы по перемещению заряда Q из точки поля с потенциалом (pt в точку с потенциалом <р0 равна
^ = С(фоФ1). О)
Бесконечная равномерно заряженная нить с линейной плотностью заряда т создает аксиально-симметричное поле напряженностью £=т/(27гее0г). Напряженность и потенциал этого поля d
связаны соотношением £= , откуда d
Edr. Разность
dr
потенциалов точек поля на расстоянии г, и г0 от нити
Г0


Фо-ф.= -
£dr =
т f dr т г*
-= In
2леео J г 2пеео го
г

И In
Го
i
Т
Фо-<Р1 = П
2Л6£о

(2)
Г2
(Р0-(Р2 = — Ь
2я££0 г0
Подставляя в формулу (1) найденное выражение для разности потенциалов из (2), определим работу, совершаемую внешними силами по перемещению заряда из точки, находящейся на расстоянии 1 м, до точки, расположенной на расстоянии 0,1 м от нити:
2л££о го’

• 10'J Дж.
, 1 • 10’9 Кл 1 • 1О’€ Кл/м In 10 , .
А1 = — =4,1
2 3,14 8,85 1012 Ф/м
„ 1 • 10"9 ■ 1 • 10€ In 10
Вычислим на калькуляторе выражение —■ по
2 3,14 8,85 10-12
программе
1[вп|9[7ч1И 1®б[Н10 югаа 2 0EI008,85R 1|вп] 12I/-/IR
Показания индикатора: 4,14087 10 5, т. е. 4,1 • 10“5 Дж.
Работа по перемещению заряда на последних 10 см пути равна
С т, Г2
Л2= In -;
2леео г0
, 1 • Ю 9 Кл 10 б Кл/м 1п2 , _ _ , „
Л2 = 7 - = 1,25 • 10'5 Дж.
2 3,14 8,85 10-12 Ф/м
Ответ: Л1 = 4,1 ' 10 5 Дж; Л2=1,25 • 10 5 Дж.
-
К одной из обкладок плоского конденсатора прилегает стеклянная плоскопараллельная пластинка (£1 = 7) толщиной 9 мм. После того как конденсатор отключили от источника напряжения 220 В и вынули стеклянную пластинку, между обкладками установилась разность потенциалов 976 В. Определить зазор между обкладками и отношение конечной и начальной энергии конденсатора.
Дано: С7!=220 В; (72=976 В; dj = 9 103 м; £1 = 7; е2=1.
Найти: do; W\/W2.
Решение. После отключения конденсатора и удаления стеклянной пластинки заряд на его обкладках остается неизменным, т. е. выполняется равенство
Cit7i = C2t/2, (1)
где С\ и С2 — электроемкости конденсатора в начальном и конечном случае.
По условию конденсатор вначале является слоистым и его электроемкость определяется по формуле
Eg ‘ S

(2)
G= —
di dodi
— +
£1 Е2
где 5 — площадь обкладок; d0 — зазор между ними, dx — толщина стеклянной пластинки, Ej и е2 — диэлектрические проницаемости стекла и воздуха соответственно.

E2£oS
После удаления стеклянной пластинки электроемкость конденсатора
(3)
Подставляя (2) и (3) в (1), получим
£о5С/1 £2£o5L/2
d\ do d\ dQ
£1 £2
откуда
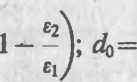





“о—
U2-Ui
976 В 9 IO-3
(976 - 220) В
м
1-’|=1 • 10’2 7/
M.
Начальная и конечная энергии конденсатора
CiU2. C2u22
W\=—; W2=—.
2 2
Тогда отношение этих энергий W2/Wi = C2U2/(CiUl). Учитывая (1), получим
W2 U2 W2 976 В . . .
——• — = 4 44
Wi Uif Wi 220 В
Ответ: do=l ' Ю“2 м; FF2/FFi=4,44.
-
Батарею из двух конденсаторов емкостью 400 и 500 пФ соединили последовательно и включили в сеть с напряжением 220 В. Потом батарею отключили от сети, конденсаторы разъединили и соединили параллельно обкладками, имеющими одноименные заряды. Каким будет напряжение на зажимах полученной батареи?
Дано: £7j = 220 В; Cj=400 пФ; С2=500 пФ.
Найти: U2.
Решение. У последовательно соединенных конденсаторов заряды на обкладках равны по модулю 61 = 62=6 и заряд батареи равен заряду одного конденсатора. Емкость батареи последовательно соединенных конденсаторов определяется по формуле п
1/С= £ 1/С«. Для батареи из двух конденсаторов
С=С, • С2/(С, + С2),
а их заряд
6 = СС/1 = С1С2С/1/(С1 + С2). (1)
При отключении конденсаторов их заряд сохраняется. У параллельно соединенных конденсаторов заряд батареи равен сумме зарядов конденсаторов 6=61 + 62» а емкость — сумме емкостей
С' = С\ + С2.
Напряжение на зажимах батареи из двух параллельно соединенных конденсаторов
Г 7 — R — _ 3^ /п\
2CCl + C2Cl-hC2' '
Подставляя (1) в (2), получаем
2CjC2?7i
(^1 + С2)
гт 2 4 5 • Ю-20 Ф2 • 220 В
tf2 = — - =108,6 В.
92 1О20 Ф2
Ответ'. t/2= 108,6 В.
-
Заряд конденсатора 1 мкКл, площадь пластин 100 см2, зазор между пластинками заполнен слюдой. Определить объемную плотность энергии поля конденсатора и силу притяжения пластин.
Дано: 6=Ю 6 Кл; 5= 10“2 м2; е=6.
Найти: >v; F.

(1)
Решение. Сила притяжения между двумя разноименно заряженными обкладками конденсатора уг .“о£2 5 ” 2
где Е — напряженность поля конденсатора; S — площадь обкладок конденсатора; е — диэлектрическая проницаемость слюды; Eq — электрическая постоянная.

(2)
Напряженность однородного поля плоского конденсатора _ ff Q Е==. ££q EEqS
где o=QIS — поверхностная плотность заряда. Подставляя (2) в (1), получаем
о2 Ю“12 Кл2
— = 0,94 Н. 2&£qS 2 6 8,85 10“12 Ф/м 10“2 м2
Объемная плотность энергии электрического поля

(3)
££qE2
W= — .
2
Подставляя (2) в (3), получаем
Q2 ю12 Кл2 -
w=——w=- —- = 94,2 Дж/м3.
2££0S2 2 • 6 8,85 10“12 Ф/м 10“* м4
Ответ: J’=0,94 Н; w=94,2 Дж/м.
-
В медном проводнике сечением 6 мм и длиной 5 м течет ток. За 1 мин в проводнике выделяется 18 Дж теплоты. Определить напряженность поля, плотность и силу электрического тока в проводнике.
Дано: 5=6 • 106 м2; 1=5 м; /=60 с; Q= 18 Дж; р = 1,7 • 10 8 Ом ■ м.
Найти: £; j; J.
Решение. Для решения задачи используем законы Ома и Джоуля — Ленца. Закон Ома в дифференциальной форме имеет вид
(о где j — плотность тока; Е — напряженность доля; у — удельная проводимость.
Закон Джоуля — Ленца
Q^Rt. (2)
Здесь J — сила тока, t — время,
R=p' (3)
д
— сопротивление проводника, где р, I, S — удельное сопротивление, длина и площадь поперечного сечения проводника соответственно.
Силу тока J находим из (2) с учетом (3):
т [q [qS I 18 Дж 6 10-6 м2
J= /—= / ; 7= -=4,6 A.
у Rt у pit у 1,7 10 8 Ом м 5 м 60 с
По определению, плотность тока равна j=J[S\
j=4,6 А/(6 • 10"6 м2) = 7,7 • 105 А/м2.
Напряженность поля в проводнике определим из (1), учитывая, что у=\1р.
E=j- р; Е=7,7 • 105 А/м2 • 1,7 КГ8 Ом • м=1,3 • 10'2 В/м.
Ответ: Е=1,3 10“2 В/м; J=4,6 A; 7=7,7 ■ 105 А/м2.
-
Внутреннее сопротивление аккумулятора 2 Ом. При замыкании его одним резистором сила тока равна 4 А, при замыкании другим — 2 А. Во внешней цепи в обоих случаях выделяется одинаковая мощность. Определить электродвижущую силу аккумулятора и внешние сопротивления.
Дано: г-2 Ом; 7] = 4 A; J2—2 A; NX=N2.
Найти: <5 ; 2^; R2-
Решение. Закон Ома для замкнутой (полной) цепи имеет вид
где г — внутреннее сопротивление источника тока; & — э. д. с. аккумулятора; R}iiR2 — внешние сопротивления цепей.
Уравнения (1) представим в виде
<5=Л(А, + г); 6=Л№+г). (2)
Из равенства> (2) следует, что
71(А1+г)=Л№+г). (3)
Мощность, выделяемая во внешней цепи в первом и втором случаях, соответственно равна
N2=JiR2.
Из условия равенства мощностей следует, что

Решая совместно уравнения (3) и (4), получаем

(4)

(5)
Л 2 А 2 Ом , _ Л 4 А • 2 Ом л _
— = 1 Ом, R2= = 4 Ом.
4 А 2 А
Подставляя (5) в (2), получаем
Ответ: & = 12 В; Rt= 1 Ом; Л2 = 4 Ом.
-
Электродвижущая сила батареи равна 20 В. Коэффициент полезного действия батареи составляет 0,8 при силе тока 4 А. Чему равно внутреннее сопротивление батареи?
Дано: £ =20 В; >7 = 0,8; .7=4 А.
Найти: г.
Решение. Коэффициент полезного действия источника тока t] равен отношению падения напряжения во внешней цепи к его электродвижущей силе.
откуда
(2)
Используя выражение закона Ома для замкнутой цепи J= £/(Л+г), получаем
Подставляя (2) в (3) и выполняя преобразования, находим
ё(1-п) 20 в (1-0,8)
г= : г= =1 Ом.
Ответ: г— 1 Ом.
-
По двум бесконечно длинным прямолинейным проводникам, находящимся на расстоянии 50 см друг от друга, в одном направлении текут токи J\ и J2 силой по 5 А. Между проводниками на расстоянии 30 см от первого расположен кольцевой проводник с током J3 силой 5 А (рис. 3). Радиус кольца 20 см. Определить индукцию и напряженность магнитного поля, создаваемого токами в центре кольцевого проводника.
Дано: J1=J2=J3=J=5 А; ^=0,2 м; г3=0,2 м.
Найти: В\ Н.
Решение. В соответствии с принципом суперпозиции индукция результирующего магнитного поля в точке А равна
В = Bj 4-Вг + В3, (1)
где Bi и В2 — индукции полей, создаваемых соответственно токами Ji и J2, направленными за плоскость рисунка; Вз — индукция поля, создаваемая кольцевым током. Как видно из рис. 3, векторы В) и Bi направлены по одной прямой в противоположные стороны, поэтому их сумма В, 4-82 = 812 равна по модулю
В{2—В2 — Bi. (2)

(3)
Индукция поля, создаваемого бесконечно длинным проводником с током,

где До — магнитная постоянная; д — магнитная проницаемость
о\——; В2———,
2nr\ 2itr2





п л12=——
2л
5>
_ДДоЛП-Г2)
2л Г| г2
•(4)
Рис. 3
среды (для воздуха д= 1); гь г2 — расстояния от проводников до центра кольца. Подставляя (3) в (2), получаем
Индукция поля, создаваемого кольцевым проводником с током,
^3=—, (5)
2z3
где г3 — радиус кольца.
Как видно из рис. 3, векторы В 2 и В3 взаимно перпендикулярны, поэтому В = + или, учитывая выражения (4) и (5), имеем
_ /W / (п-^)2 1
1 12,56 10“7 Гн/м 5 А / (0,3 - 0,2)2 м2 Г”
“ 2 \ 3,142 0,32 0,22 м* ' 0,22 М2
= 15,7 • 10'6 Тл = 15,7 мкТл.
Вычислим на калькуляторе выражение

12,56■10“75
2
(0,3-0,2)2 1
3,142 0,32 • 0,22+0,22
по программе
[00,3 00,200 0|Гш1 0 □ В 0,300g00,2
F х2
х^п| 12,56[ВП| 7|/^/||х|5 [Z| 2 Р|[Ё]|х-»П
Показания индикатора: 1,57111 10 5, т. е. 15,67 мкТл.
Напряженность магнитного поля
ТТ В гг 15,7 ‘ 10“б Тл 1О_А,
Н——; Н= =12,5 А/м.
д/4) 1 12,56 10 7 Гн/м
Ответ: В= 15,7 мкТл; Н= 12,5 А/м.
-
Электрон, пройдя ускоряющую разность потенциалов 88 кВ, влетает в однородное магнитное поле перпендикулярно его линиям индукции. Индукция поля равна 0,01 Тл. Определить радиус траектории электрона.
Дано: £7=88 кВ; В=0,01 Тл; е=1,6 • 10
19 Кл.
Найти: г.
Решение. В магнитном поле с индукцией В на электрон, движущийся со скоростью v перпендикулярно В, действует сила Лоренца
F=evB, (1)
которая обусловливает центростремительное ускорение электрона при его движении по окружности:
evB=—, (2)
г где т — масса электрона; е — его заряд; г — радиус траектории его движения.
Пройдя ускоряющую разность потенциалов (7, электрон приобретает кинетическую энергию mv2/2, равную работе А сил электрического поля m»2l2 — eU. Отсюда находим скорость электрона:
_ДДоЛП-Г2)
2л Г| г2
•(4)
Рис. 3
среды (для воздуха д= 1); гь г2 — расстояния от проводников до центра кольца. Подставляя (3) в (2), получаем
Индукция поля, создаваемого кольцевым проводником с током,
^3=—, (5)
2z3
где г3 — радиус кольца.
Как видно из рис. 3, векторы В 2 и В3 взаимно перпендикулярны, поэтому В = + или, учитывая выражения (4) и (5), имеем
_ /W / (п-^)2 1
1 12,56 10“7 Гн/м 5 А / (0,3 - 0,2)2 м2 Г”
“ 2 \ 3,142 0,32 0,22 м* ' 0,22 М2
= 15,7 • 10'6 Тл = 15,7 мкТл.
Вычислим на калькуляторе выражение

12,56■10“75
2
(0,3-0,2)2 1
3,142 0,32 • 0,22+0,22
по программе
[00,3 00,200 0|Гш1 0 □ В 0,300g00,2
F х2
х^п| 12,56[ВП| 7|/^/||х|5 [Z| 2 Р|[Ё]|х-»П
Показания индикатора: 1,57111 10 5, т. е. 15,67 мкТл.
Напряженность магнитного поля
ТТ В гг 15,7 ‘ 10“б Тл 1О_А,
Н——; Н= =12,5 А/м.
д/4) 1 12,56 10 7 Гн/м
Ответ: В= 15,7 мкТл; Н= 12,5 А/м.
-
Электрон, пройдя ускоряющую разность потенциалов 88 кВ, влетает в однородное магнитное поле перпендикулярно его линиям индукции. Индукция поля равна 0,01 Тл. Определить радиус траектории электрона.
Дано: £7=88 кВ; В=0,01 Тл; е=1,6 • 10
19 Кл.
Найти: г.
Решение. В магнитном поле с индукцией В на электрон, движущийся со скоростью v перпендикулярно В, действует сила Лоренца
F=evB, (1)
которая обусловливает центростремительное ускорение электрона при его движении по окружности:
evB=—, (2)
г где т — масса электрона; е — его заряд; г — радиус траектории его движения.
Пройдя ускоряющую разность потенциалов (7, электрон приобретает кинетическую энергию mv2/2, равную работе А сил электрического поля m»2l2 — eU. Отсюда находим скорость электрона:
_ДДоЛП-Г2)
2л Г| г2
•(4)
Рис. 3
среды (для воздуха д= 1); гь г2 — расстояния от проводников до центра кольца. Подставляя (3) в (2), получаем
Индукция поля, создаваемого кольцевым проводником с током,
^3=—, (5)
2z3
где г3 — радиус кольца.
Как видно из рис. 3, векторы В 2 и В3 взаимно перпендикулярны, поэтому В = + или, учитывая выражения (4) и (5), имеем
_ /W / (п-^)2 1
1 12,56 10“7 Гн/м 5 А / (0,3 - 0,2)2 м2 Г”
“ 2 \ 3,142 0,32 0,22 м* ' 0,22 М2
= 15,7 • 10'6 Тл = 15,7 мкТл.
Вычислим на калькуляторе выражение

12,56■10“75
2
(0,3-0,2)2 1
3,142 0,32 • 0,22+0,22
по программе
[00,3 00,200 0|Гш1 0 □ В 0,300g00,2
F х2
х^п| 12,56[ВП| 7|/^/||х|5 [Z| 2 Р|[Ё]|х-»П
Показания индикатора: 1,57111 10 5, т. е. 15,67 мкТл.
Напряженность магнитного поля
ТТ В гг 15,7 ‘ 10“б Тл 1О_А,
Н——; Н= =12,5 А/м.
д/4) 1 12,56 10 7 Гн/м
Ответ: В= 15,7 мкТл; Н= 12,5 А/м.
-
Электрон, пройдя ускоряющую разность потенциалов 88 кВ, влетает в однородное магнитное поле перпендикулярно его линиям индукции. Индукция поля равна 0,01 Тл. Определить радиус траектории электрона.
Дано: £7=88 кВ; В=0,01 Тл; е=1,6 • 10
19 Кл.2л Г| г2
•(4)
Рис. 3
среды (для воздуха д= 1); гь г2 — расстояния от проводников до центра кольца. Подставляя (3) в (2), получаем
Индукция поля, создаваемого кольцевым проводником с током,
^3=—, (5)
2z3
где г3 — радиус кольца.
Как видно из рис. 3, векторы В 2 и В3 взаимно перпендикулярны, поэтому В = + или, учитывая выражения (4) и (5), имеем
_ /W / (п-^)2 1
1 12,56 10“7 Гн/м 5 А / (0,3 - 0,2)2 м2 Г”
“ 2 \ 3,142 0,32 0,22 м* ' 0,22 М2
Электрон, пройдя ускоряющую разность потенциалов 88 кВ, влетает в однородное магнитное поле перпендикулярно его линиям индукции. Индукция поля равна 0,01 Тл. Определить радиус траектории электрона.
Найти: г.
Решение. В магнитном поле с индукцией В на электрон, движущийся со скоростью v перпендикулярно В, действует сила Лоренца
F=evB, (1)
которая обусловливает центростремительное ускорение электрона при его движении по окружности:
evB=—, (2)
г где т — масса электрона; е — его заряд; г — радиус траектории его движения.
Пройдя ускоряющую разность потенциалов (7, электрон приобретает кинетическую энергию mv2/2, равную работе А сил электрического поля m»2l2 — eU. Отсюда находим скорость электрона:

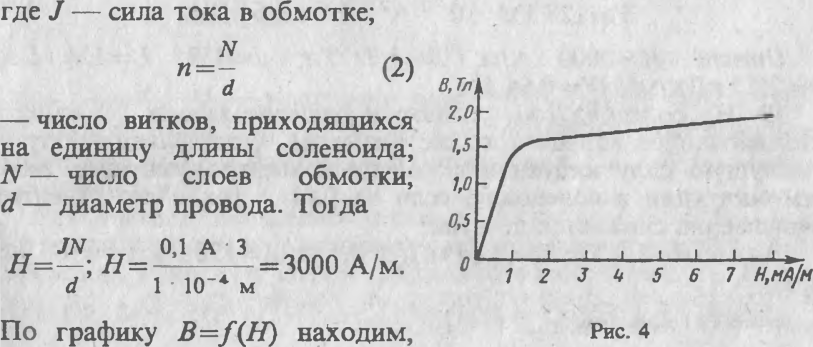

2 88 103 В 9,1 10"31 кг п t = 0,1 М.
1,6 10"19 Кл
Н= J • и,
Из уравнения (2) с учетом (3) найдем радиус траектории:
1 I1U т
г=- / ;
В \ е
1
Г— —
1 10"2 Тл
Ответ: г=0,1 м.
-
Соленоид длиной 20 см и диаметром 4 см имеет плотную трехслойную обмотку из провода диаметром 0,1 мм. По обмотке соленоида течет ток 0,1 А. Зависимость B=j\H) для материала сердечника приведена на рис. 4. Определить напряженность и индукцию поля в соленоиде, магнитную проницаемость сердечника, индуктивность соленоида, энергию и объемную плотность энергии поля соленоида.
Дано: 7=0,2 м; Л = 0,04 м; 7V=3; d=l • 104м; J=0,l А.
Найти: Н\ В\ ц; L; w.
Решение. Поле внутри соленоида можно считать однородным. В этом случае напряженность поля
(1)
что напряженности 3000 А/м соответствует индукция 1,7 Тл. Используя связь между индукцией и напряженностью
(3)
определим магнитную проницаемость

=450.
1,7 Тл
12,56 10"7 Гн/м 3000 А/м
Индуктивность соленоида
L=/W>2 ■/ •$> (4)
где / — длина, S=тг£>2/4 — площадь поперечного сечения солено- ида. Учитывая (2), получаем
№ nD2
Ь=Щ1о— * I • —; (5)




450-12,56 10“7
Гн/м З2 0,2 м • 3,14 42 • 10“4
4 1 10“в м2
—=128 Гн.
Объемная плотность энергии магнитного поля
или
Подставляя числовые данные в (7), получаем
W= 128 Гн ■ 10’2 А2 • 0,5 = 0,64 Дж.
Ответ'. /7=3000 А/м; /?=1,7 Тл; /х=450; £=128 Гн; и>=2,55 кДж/м3; 17=0,64 Дж.
-
На соленоид (см. условие и решение задачи 12) надето изолированное кольцо того же диаметра. Определить электродвижущую силу индукции в кольце и электродвижущую силу самоиндукции в соленоиде, если за 0,01 с ток в его обмотке равномерно снижается до нуля.
Дано: В= 1,7 Тл; D = 0,04 м; Л = 0,1 A; L= 128 Гн; Д/= 10"2 с; Л=0.
Найти: 8$.
Решение. По условию за время А/=0,01 с сила тока в обмотке соленоида равномерно уменьшается от 0,1 А до нуля, поэтому магнитный поток, пронизывающий площадь кольца S=7lD2/4, уменьшается от Ф] = В5 до Ф2=0. Электродвижущая сила индукции, возникающая в кольце,
Дф Фз-Ф! Ф1 В ’ TlD2
О i == j
Л/ Аг Ar 4 АГ
с 1,7 Тл 3,14 16 • 10’4 м2 л л л
-
=- >. =0.2 В
Электродвижущая сила самоиндукции £$, возникающая в соле- , dJ
ноиде при выключении тока в нем, <£$= — L—. Так как при dr
выключении сила тока уменьшается до нуля равномерно, то
dJ AJ J\
dr Ar Ar Ar
Тогда



LJi
Ar
128 Гн 0,1 A
0,01 c
=1280 B.
Ответ: 6\=0,21 B; 6^=1280 B.
-
Виток радиусом 5 см с током 1 А помещен в однородное магнитное поле напряженностью 5000 А/м так, что нормаль к витку составляет угол 60° с направлением поля. Какую работу совершат силы поля при повороте витка в устойчивое положение?
Дано: г=0,05 м; J=1 А; Н— 5000 А/м; а=60°.
Решение. Работа А при повороте витка с током J в магнитном поле
A = J ДФ. (1)
Здесь АФ=Ф2—Ф1 — изменение магнитного потока сквозь площадь витка 5=тгг2; Ф1 =В ’ S ' cos а — магнитный поток, пронизывающий виток в начальном положении, где а — угол между векторами п и В.
Устойчивым положением витка в магнитном поле является такое, при котором направление нормали к нему совпадает с вектором индукции, т. е. cosa=l. Следовательно, Ф2=В S. Таким образом, ДФ=2?тсг2 • (1 — cos а). Учитывая, что имеем


АФ = р-^Нпг2 (1 — cos а)
(2)
Подставляя (2) в (1), получаем
А = У/х/ХоЯлг2 (1 — cos а);
А = 1 А * 1 * 12,56 * 10’7 Гн/м • 5 • 103 А/м • 3,14 • 25 • 10"4 м2 х х (1-0,5)=2,46 • 10"5 Дж.
Ответ: Л = 2,46 • 10"5 Дж.
КОНТРОЛЬНАЯ РАБОТА № 2
-
В вершинах квадрата со стороной 0,1 м расположены равные одноименные заряды. Потенциал создаваемого ими поля в центре квадрата равен 500 В. Определить заряд. -
В вершинах квадрата со стороной 0,5 м расположены заряды одинаковой величины. В случае, когда два соседних заряда положительные, а два других — отрицательные, напряженность поля в центре квадрата равна 144 В/м. Определить заряд. -
В вершинах квадрата со стороной 0,1 м помещены заряды по 0,1 нКл. Определить напряженность и потенциал поля в центре квадрата, если один из зарядов отличается по знаку от остальных. -
Пространство между двумя параллельными бесконечными плоскостями с поверхностной плотностью зарядов 4-5 10“8 и —9 * 10“8 Кл/м2 заполнено стеклом. Определить напряженность поля: а) между плоскостями; б) вне плоскостей. -
На расстоянии 8 см друг от друга в воздухе находятся два заряда по 1 нКл. Определить напряженность и потенциал полу в точке, находящейся на расстоянии 5 см от зарядов. -
Две параллельные плоскости одноименно заряжены с пове рхностной плотностью зарядов 2 и 4 нКл/м2. Определить напря женность поля: а) между плоскостями; б) вне плоскостей. -
Если в центр квадрата, в вершинах которого находятс заряды по 4-2 нКл, поместить отрицательный заряд, то резуль тирующая сила, действующая на каждый заряд, будет равн: нулю. Вычислить числовое значение отрицательного заряда. -
Заряды по 1 нКл помещены в вершинах равносторонней треугольника со стороной 0,2 м. Равнодействующая сил, действу ющих на четвертый заряд, помещенный на середине одной и: сторон треугольника, равна 0,6 мкН. Определить этот заряд напряженность и потенциал поля в точке его расположения. -
Два шарика массой по 2 мг подвешены в общей точке на нитях длиной 0,5 м. Шарикам сообщили заряд и нити разошлись на угол 90°. Определить напряженность и потенциал поля в точке подвеса шарика.
. 10. Два одинаковых заряда находятся в воздухе на расстоянии 0,1 м друг от друга. Напряженность поля в точке, удаленной на расстоянии 0,06 м от одного и 0,08 м от другого заряда, равна 10 кВ/м. Определить потенциал поля в этой точке и значение зарядов.
-
Пылинка массой 8-Ю"15 кг удерживается в равновесии между горизонтально расположенными обкладками плоского конденсатора. Разность потенциалов между обкладками 490 В, а зазор между ними 1 см. Определить, во сколько раз заряд пылинки больше элементарного заряда. -
В поле бесконечной равномерно заряженной плоскости с поверхностной плотностью заряда 10 мккл/м2 перемещается заряд из точки, находящейся на расстоянии 0,1 м от плоскости, в точку на расстоянии 0,5 м от нее. Определить заряд, если при этом совершается работа 1 мДж. -
Какую работу нужно совершить, чтобы заряды 1 и 2 нКл, находившиеся на расстоянии 0,5 м, сблизились до 0,1 м? -
Поверхностная плотность заряда бесконечной равномерно заряженной плоскости равна 30 нКл/м2. Определить поток вектора напряженности через поверхность сферы диаметром 15 см, рассекаемой этой плоскостью пополам. -
Заряд 1 нКл переносится из бесконечности в точку, находящуюся на расстоянии 0,1 м от поверхности металлической сферы радиусом 0,1 м, заряженной с поверхностной плотностью 10 Кл/м2. Определить работу перемещения заряда. -
Заряд 1 нКл притянулся к бесконечной плоскости, равномерно заряженной с поверхностной плотностью 0,2 мкКл/м2. На каком расстоянии от плоскости находился заряд, если работа сил поля по его перемещению равна 1 мкДж? -
Какую работу совершают силы поля, если одноименные заряды 1 и 2 нКл, находившиеся на расстоянии 1 см, разошлись до расстояния 10 см? -
Со скоростью 2 10 м/с электрон влетает в пространство между обкладками плоского конденсатора в середине зазора в направлении, параллельном обкладкам. При какой минимальной разности потенциалов на обкладках электрон не вылетит из конденсатора, если длина конденсатора 10 см, а расстояние между его обкладками 1 см? -
Заряд — 1 нКл переместился в поле заряда +1,5 нКл из точки с потенциалом 100 В в точку с потенциалом 600 В. Определить работу сил поля и расстояние между этими точками. -
Заряд 1 нКл находится на расстоянии 0,2 м от бесконечно длинной равномерно заряженной нити. Под действием поля нити заряд перемещается на 0,1 м. Определить линейную плотность заряда нити, если работа сил прля равна 0,1 мкДж. -
Конденсатор с парафиновым диэлектриком заряжен до
разности потенциалов 150 В. Напряженность поля 6 ' 106 В/м, 4-279 81
площадь пластин 6 см2. Определить емкость конденсатора и поверхностную плотность заряда на обкладках.
-
Вычислить емкость батареи, состоящей из трех конденсаторов емкостью 1 мкФ каждый, при всех возможных случаях их соединения. -
Заряд на каждом из двух последовательно соединенных конденсаторов емкостью 18 и 10 пкФ равен 0,09 нКл. Определить напряжение: а) на батарее конденсаторов; б) на каждом конденсаторе. -
Конденсатор емкостью 6 мкФ последовательно соединен с конденсатором неизвестной емкости и они подключены к источнику постоянного напряжения 12 В. Определить емкость второго конденсатора и напряжения на каждом конденсаторе, если заряд батареи 24 мкКл. -
Два конденсатора одинаковой емкости по 3 мкФ заряжены один до напряжения 100 В, а другой — до 200 В. Определить напряжение между обкладками конденсаторов, если их соединить параллельно: а) одноименно; б) разноименно заряженными обкладками. -
Плоский воздушный конденсатор заряжен до разности потенциалов 300 В. Площадь пластин 1 см2, напряженность поля в зазоре между ними 300 кВ/м. Определить поверхностную плотность заряда на пластинах, емкость и энергию конденсатора. -
Найти объемную плотность энергии электрического поля, создаваемого заряженной металлической сферой радиусом 5 см на расстоянии 5 см от ее поверхности, если поверхностная плотность заряда на ней 2 мкКл/м . -
Площадь пластин плоского слюдяного конденсатора 1,1 см2, зазор между ними 3 мм. При разряде конденсатора выделилась энергия 1 мкДж. До какой разности потенциалов был заряжен конденсатор? -
Энергия плоского воздушного конденсатора 0,4 нДж, разность потенциалов на обкладках 600 В, площадь пластин 1 см2. Определить расстояние между обкладками, напряженность и объемную плотность энергии поля конденсатора. -
Под действием силы притяжения 1 мН диэлектрик между обкладками конденсатора находится под давлением 1 Па. Определить энергию и объемную плотность энергии поля конденсатора, если расстояние между его обкладками 1 мм. -
Плотность тока в никелиновом проводнике длиной 25 м равна 1 МА/м2. Определить разность потенциалов на концах проводника. -
Определить плотность тока, текущего по проводнику длиной 5 м, если на концах его поддерживается разность потенциалов 2 В. Удельное сопротивление материала 2 мкОм • м. -
Напряжение на концах проводника сопротивлением 5 Ом за 0,5 с равномерно возрастает от 0 до 20 В. Какой заряд проходит через проводник за это время? -
Температура вольфрамовой нити электролампы 2000 °C, диаметр 0,02 мм, сила тока в ней 4 А. Определить напряженность поля в нити. -
На концах никелинового проводника длиной 5 м поддерживается разность потенциалов 12 В. Определить плотность тока в проводнике, если его температура 540 °C. -
Внутреннее сопротивление аккумулятора 1 Ом. При силе тока 2 А его к. п. д. равен 0,8. Определить электродвижущую силу аккумулятора. -
Определить электродвижущую силу аккумуляторной батареи, ток короткого замыкания которой 10 А, если при подключении к ней резистора сопротивлением 2 Ом сила тока в цепи равна 1 А. -
Электродвижущая сила аккумулятора автомобиля 12 В. При силе тока 3 А его к.п. д. равен 0,8. Определить внутреннее сопротивление аккумулятора. -
К источнику тока подключают один раз резистор сопротивлением 1 Ом, другой раз — 4 Ом. В обоих случаях на резисторах за одно и то же время выделяется одинаковое количество теплоты. Определить внутреннее сопротивление источника тока. -
Два одинаковых источника тока соединены в одном случае последовательно, в другом — параллельно и замкнуты на внешнее сопротивление 1 Ом. При каком внутреннем сопротивлении источника сила тока во внешней цепи будет в обоих случаях одинаковой? -
Два бесконечно длинных прямолинейных проводника с токами 6 и 8 А расположены перпендикулярно друг другу. Определить индукцию и напряженность магнитного поля на середине кратчайшего расстояния между проводниками, равного 20 см. -
По двум бесконечно длинным прямолинейным параллельным проводникам, расстояние между которыми 15 см, в одном направлении текут токи 4 и 6 А. Определить расстояние от проводника с меньшим током до геометрического места точек, в котором напряженность магнитного поля равна нулю. -
Решить задачу 42 для случая, когда токи текут в противоположных направлениях. -
По двум бесконечно длинным прямолинейным параллельным проводникам текут токи 5 и 10 А в одном направлении. Геометрическое место точек, в котором индукция магнитного поля равна нулю, находится на расстоянии 10 см от проводника с меньшим током. Определить расстояние между проводниками.