ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 119
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ГЛАВА 2. УРАВНЕНИЯ И НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ
У р о к 24 Дата:
ПОНЯТИЕ ЦЕЛОГО УРАВНЕНИЯ И ЕГО СТЕПЕНИ
Цели: ввести понятие целого уравнения и его степени; формировать умение определять степень целого уравнения и решать целые уравнения не выше второй степени.
Ход урока
I. Организационный момент.
II. Устная работа.
Определите, сколько корней имеет уравнение:
а) 2х + 1 = 0; д) 3х + 1 = 5 + 3х;
б) х2 – 5 = 0; е) х2 + 2х + 1 = 0;
в) х5 + 1 = 0; ж) х2 + х + 10 = 0;
г) х6 + 2 = 0; з) 1 – 4х = 1 – 4х.
III. Объяснение нового материала.
На этом уроке достаточно ввести понятие целого уравнения и его степени; рассмотреть примеры приведения целого уравнения к виду Р (х) = 0, где Р (х) – многочлен; обратиться к решению целых уравнений первой и второй степени. Вопрос о методах решения целых уравнений выше второй степени целесообразно изучить на следующем уроке.
Объяснение проводится по следующей с х е м е:
1. В в е д е н и е п о н я т и я целого уравнения.
После формирования определения данного понятия необходимо дать учащимся задание на распознавание целых уравнений.
З а д а н и е. Какие из следующих уравнений являются целыми? Ответ объясните.
а) х4 + 2х3 – 7 = 0; г) – 5х3 = 0;
б) 4х10 = 0,7х8; д)
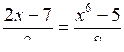 ;
;в) (х – 1) (3х2 + 5) = х4 + 2; е)
2. В в е д е н и е п о н я т и я степени целого уравнения.
После введения данного понятия дать учащимся задание на определение степени целого уравнения.
З а д а н и е. Какова степень уравнения:
а) 2х5 + 4х – 3 = 0; г) – 5х = 7;
б) х7 + 5х = 0; д) (2х + 1) (х – 7) – х = 0;
в) х11
= х3; е) 5х2 – 4х2 (1 – х) = 0?
3. Р а с с м о т р е н и е р е ш е н и я линейных и квадратных уравнений как целых уравнений первой и второй степени соответственно.
Необходимо, чтобы учащиеся осознали следующее:
1) изученные ранее линейные и квадратные уравнения являются целыми уравнениями первой и второй степени соответственно;
2) уравнение первой степени может иметь не более одного корня;
3) уравнение второй степени может иметь не более двух корней.
IV. Формирование умений и навыков.
На этом уроке учащиеся выполняют задания на определение степени целого уравнения и приведение целых уравнений к виду Р (х) = 0. Для решения нужно предлагать им уравнения не выше второй степени.
Упражнения:
1. Приведите уравнение к виду Р (х) = 0 и определите его степень:
а) 2х (1 – 3х) + (х + 4) (х2 – 1) = 0;
б) (х3 – 2) (1 + 3х2) – 3 (х4 – 1) = 5;
в) (х – 1) (х + 2) (х – 3) = х – 4х2 (2 – х5).
2. Какие из следующих чисел –3; –2; –1; 0; 1; 2; 3 являются корнями уравнения:
а) х3 – 4х = 0;
б) х2 (х + 1) + (х + 4) = 4;
в) х4 – 5х2 + 4 = 0?
3. № 266 (а, в), № 267 (б, г).
4. № 268.
Р е ш е н и е
5х6 + 6х4 + х2 + 4 = 0.
Выражения 5х6, 6х4 и х2 могут принимать только неотрицательные значения при любых значениях х. Поэтому выражение 5х6 + 6х4 + х2 + 4 при любых значениях х принимает только положительные значения, а значит, не может быть равно нулю, то есть уравнение 5х6 + 6х4 + х2 + 4 = 0 не имеет решений.
Д о п о л н и т е л ь н о: № 270.
Р е ш е н и е
Пусть ребро куба равно х см, тогда его объем равен х3 см3. Если увеличить ребро куба на 3 см, то оно станет равно (х + 3) см, а объем куба будет равен (х + 3)3 см3.
Составим и решим уравнение:
(х + 3)3 = х3 + 513;
х3 + 9х2 + 27х + 27 = х3 + 513;
9х2 + 27х – 486 = 0;
х2 + 3х – 54 = 0;
х = 6;
х = – 9 – не удовлетворяет условию задачи.
О т в е т: 6 см.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какое уравнение называется целым?
– Что такое степень целого уравнения?
– Какова степень уравнения 2х3 – 5 + х6 = 0?
– Сколько корней может иметь целое уравнение первой степени? второй степени?
Домашнее задание: № 266 (б, г), № 267 (а, в), № 269.
Д о п о л н и т е л ь н о: № 271.
У р о к 25 Дата:
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ ЦЕЛЫХ УРАВНЕНИЙ
Цели: изучить основные методы решения целых уравнений; формировать умение применять эти методы.
Ход урока
I. Организационный момент.
II. Устная работа.
№ 265.
III. Проверочная работа.
В а р и а н т 1
1. Какие из чисел: –3; –1; 0; 2; 3 – являются корнями уравнения
2х3 + х2 – 13х + 6 = 0?
2. Решите уравнение:
а)
3*. Составьте какое-либо уравнение третьей степени, имеющее корни –2; 2 и 5.
В а р и а н т 2
1. Какие из чисел: –2; –1; 0; 2; 3 – являются корнями уравнения 3х3 –
– 5х2 – 11х – 3 = 0?
2. Решите уравнение:
а) = 1; б)
3*. Составьте какое-либо уравнение третьей степени, имеющее корни 0; –3 и 5.
IV. Объяснение нового материала.
На этом уроке необходимо рассмотреть два основных метода решения целых уравнений и сделать ряд важных выводов.
1. А к т у а л и з а ц и я з н а н и й.
В о п р о с ы у ч а щ и м с я:
– Какое уравнение называется целым?
– Что такое степень целого уравнения?
– Как решаются целые уравнения первой и второй степени?
2. В ы д е л е н и е м е т о д о в решения целых уравнений.
Необходимо, чтобы учащиеся осознали, что им уже известны приемы решения целых уравнений первой и второй степени. Сообщить учащимся, что существуют также формулы корней целых уравнений третьей и четвертой степени, но их использование на практике неудобно.
Существуют два основных метода решения целых уравнений выше второй степени:
| | |
| Метод разложения на множители П р и м е р: х5 – 4х3 = 0; х3 (х2 – 4) = 0; х3 = 0; или х2 – 4 = 0; х = 0. х2 = 4; х = ± 2. О т в е т: –2; 0; 2. | Метод введения новой переменной П р и м е р: 9х4 – 10х2 + 1 = 0. Пусть х2 = а, тогда 9а2 – 10а + 1 = 0; а1 = 1 и а2 = ; х2 = 1 и х2 = ; х = ± 1 и х = ± . О т в е т: ± 1, ± . |
Желательно, чтобы учащиеся занесли себе в тетради изображенную схему. Необходимо также обратить внимание учащихся, что уравнение п-й степени может иметь не более п корней.
V. Формирование умений и навыков.
На этом уроке учащиеся только начинают осваивать методы решения целых уравнений выше второй степени. Поэтому задания должны быть несложными и разбиты на две группы в соответствии с методами решения.
Упражнения:
1-я г р у п п а. Метод разложения на множители.
№ 272 (а, в, д, ж).
2-я г р у п п а. Метод введения новой переменной.
1. № 278 (а, в, д).
2. № 276 (а, в).
Р е ш е н и е
а) (2х2 + 3)2 – 12 (2х2 + 3) + 11 = 0.
З а м е н а: 2х2 + 3 = а;
а2 – 12а + 11 = 0;
а1 = 1 а2 = 11.
В е р н е м с я к з а м е н е:
| 2х2 + 3 = 1; или 2х2 = –2. Решений нет. | 2х2 + 3 = 11; 2х2 = 8; х2 = 4; х = ± 2. |
О т в е т: ± 2.
в) (х2 + х – 1) (х2 + х + 2) = 40.
З а м е н а: х2 + х – 1 = а;
а (а + 3) = 40;
а2 + 3а – 40 = 0;
а1 = –8, а2 = 5.
В е р н е м с я к з а м е н е:
| х2 + х – 1 = –8; или х2 + х + 7 = 0; D = 1 – 28 = –27. Решений нет. | х2 + х – 1 = 5; х2 + х – 6 = 0; х1 = –3, х2 = 2. |
О т в е т: –3; 2.
VI. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется степенью целого уравнения?
– Как решаются целые уравнения первой степени? второй степени?
– Существуют ли формулы для решения целых уравнений третьей и четвертой степени? Почему они редко применяются на практике?
– Какими методами могут быть решены целые уравнения выше второй степени?
– Опишите сущность каждого из методов решения целых уравнений.
Домашнее задание: № 272 (б, г, е, з), № 278 (б, г, е), № 276 (б, г).
У р о к 26 Дата:
РЕШЕНИЕ ЦЕЛЫХ УРАВНЕНИЙ РАЗЛИЧНЫМИ МЕТОДАМИ
Цель: продолжить формирование умения применять различные методы при решении целых уравнений выше второй степени.
Ход урока
I. Организационный момент.
II. Устная работа.
Определите, каким методом может быть решено каждое из данных целых уравнений:
а) 7х5 + 3х4 = 0; г)
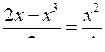 ;
;б) х4 + 3х2 – 4 = 0; д) (х2 – 5)2 + 2(х2 – 5)2 + 1 = 0;
в) х3 + х2 + х + 1 = 0; е) (х2 – 2х) (х2 + 4 – 2х) = 3.
III. Формирование умений и навыков.
На этом уроке учащиеся продолжают применять разные методы решения целых уравнений. При этом внимание уделяется не только грамотному их использованию, но и умению распознавать по внешнему виду уравнения тот метод, который целесообразно применить в данной ситуации.
Упражнения:
1. № 273 (в. д), № 279 (д), № 282 (а), № 277 (а, в), № 282 (а).
2. № 283 (а).
Р е ш е н и е
х5 + х4 – 6х3 – 6х2 + 5х + 5 = 0.
Разложим выражение, стоящее слева, на множители методом группировки. Получим:
х4 (х + 1) – 6х2 (х + 1) + 5 (х + 1) = 0;
(х + 1) (х4 – 6х2 + 5) = 0;
| х + 1 = 0; или х = –1. | х4 – 6х2 + 5 = 0; х2 = t; t2 – 6t + 5 = 0; t1 = 1, t2 = 5; х2 = 1, х2 = 5; х = ±1, х = ± . |