ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 128
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
III. Формирование умений и навыков.
Все задания можно разбить на три группы. Каждая группа будет содержать упражнения на решение всех изученных видов уравнений и неравенств. Отличие групп друг от друга состоит в уровне сложности, входящих в них уравнений и неравенств. В классе с невысоким уровнем подготовки третью группу заданий можно не выполнять.
Упражнения:
1-я г р у п п а.
1. Решите уравнение:
а)
; в) х4 + 3х2 – 4 = 0;б) х3 – 25х = 0; г) = 1.
2. Решите неравенство:
а) 2х – ≤ ; в) 1 – х2 ³ 0;
б) х2 + 2х > 0; г) (х – 3) (х + 5) < 0.
2-я г р у п п а.
1. Решите уравнение:
а) х =
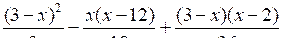;б) х6 – х4 + 5х2 – 5 = 0;
в) (х2 + х)2 – 5х2 – 5х + 6 = 0;
г)
.2. Найдите область определения функции:
а) y = ; б) y = .
3. Решите неравенство:
а) х (7 – х) (1 + х) ≥ 0; б) ≤ 0.
3-я г р у п п а.
1. Решите уравнение:
а) (х2 – 7х + 13)2 – (х – 3) (х – 4) = 1;
б) х2 + 1 = (3х2 – х – 2)2 – 2х;
в)
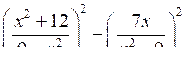= 0.2. Решите неравенство:
а)
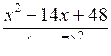< 0; б) 
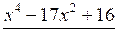≤ 0.3. При каких значениях параметра а корни уравнения х2 – 2ах +
+ (а + 1) (а – 1) = 0 принадлежат промежутку [–5; 5]?
Р е ш е н и е
Данное квадратное уравнение согласно условию должно иметь корни, значит, его дискриминант не может быть отрицательным. Найдем его:
D1 = а2 – (а + 1) (а – 1) = 1.
Получаем, что уравнение при любом а имеет два корня:
х1 = а + 1 и х2 = а – 1.
Чтобы эти корни принадлежали указанному промежутку, меньший из них должен быть не меньше –5, а больший – не больше 5. Получим систему:
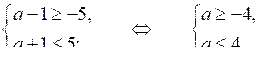
О т в е т: [–4; 4].
4. При каких значениях параметра а уравнение х2 + 2(а + 1) х + 9 = 0 имеет два различных положительных корня?
Р е ш е н и е
Чтобы данное квадратное уравнение имело два различных корня, его дискриминант должен быть положительным:
D1 = (а + 1)2 – 9 = а2 + 2а – 8;
а2 + 2а – 8 > 0.
Решая это неравенство, получим, что а (–∞; –4) (2; +∞).
По теореме Виета, произведение корней данного уравнения равно 9. Это означает, что корни имеют одинаковые знаки.
Пусть х1 и х2 – корни уравнения, тогда, по теореме Виета, х1 + х2 =
= –2 (а + 1). Чтобы эти корни были положительны, должно выполняться следующее условие:
–2 (а + 1) > 0;
а + 1 < 0;
а < –1.
С учетом выявленного выше условия получим, что а (–∞; –4).
О т в е т: (–∞; –4).
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– На какие два вида делятся рациональные уравнения?
– Какими методами решаются целые уравнения выше второй степени?
– Как решаются дробно-рациональные уравнения?
– На какие два вида делятся неравенства?
– Как решаются целые неравенства с одной переменной?
– Как решаются дробно-рациональные неравенства?
Домашнее задание: № 353 (а), № 354 (в), № 364 (б), № 377 (а), № 393 (в, д).
У р о к 37 Дата:
КОНТРОЛЬНАЯ РАБОТА № 2
В а р и а н т 1
1. Решите уравнение:
а) х3 – 81х = 0; б) = 2.
2. Решите биквадратное уравнение: х4 – 19х2 + 48 = 0.
3. Решите неравенство:
а) 2х2 – 13х + 6 < 0; б) х2 – 9 > 0; в) 3х2 – 6х + 32 > 0.
4. Решите неравенство, используя метод интервалов:
а) (х + 8) (х – 4) > 0; б) < 0.
5. При каких значениях t уравнение 3х2 + tх + 3 = 0 имеет два корня?
6.* Решите уравнение:
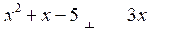+ 4 = 0.В а р и а н т 2
1. Решите уравнение:
а) х3 – 25х = 0; б)
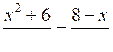= 1.2. Решите биквадратное уравнение: х4 – 4х2 – 45 = 0.
3. Решите неравенство:
а) 2х2 – х – 15 > 0; б) х2 – 16 < 0; в) х2 + 12х + 80 < 0.
4. Решите неравенство, используя метод интервалов:
а) (х + 11) (х –9) < 0; б) > 0.
5. При каких значениях t уравнение 2х2 + tх + 8 = 0 не имеет корней?
6.* Решите уравнение:
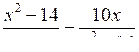= 3.В а р и а н т 3
1. Решите уравнение:
а) х3 – 36х = 0; б)
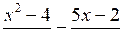= 1.2. Решите биквадратное уравнение: х4 – 13х2 + 36 = 0.
3. Решите неравенство:
а) 2х2 + 5х – 7 < 0; б) х2 – 25 > 0; в) 5х2 – 4х + 21 > 0.
4. Решите неравенство, используя метод интервалов:
а) (х + 9) (х – 5) > 0; б) < 0.
5. При каких значениях t уравнение 2х2 + tх + 2 = 0 имеет два корня?
6.* Решите уравнение:
= 2.
В а р и а н т 4
1. Решите уравнение:
а) х3 – 49х = 0; б)
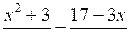= 2.2. Решите биквадратное уравнение: х4 – 17х2 + 16 = 0.
3. Решите неравенство:
а) 5х2 + 3х – 8 > 0; б) х2 – 49 < 0; в) 4х2 – 2х + 13 < 0.
4. Решите неравенство, используя метод интервалов:
а) (х + 12) (х –7) < 0; б) > 0.
5. При каких значениях t уравнение 25х2 + tх + 1 = 0 не имеет корней?
6.* Решите уравнение:
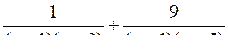
= –1.
Домашнее задание : Решить другой вариант
РЕШЕНИЕ ВАРИАНТОВ КОНТРОЛЬНОЙ РАБОТЫ
В а р и а н т 1
| 1. а) х3 – 81х = 0; | | б) = 2; |
| х (х2 – 81) = 0; | | 2(х2 – 1) – (3х – 1) = 2 · 4; |
| х = 0 или О т в е т: –9; 0; 9. | х2 – 81 = 0; х2 = 81; х = ±9. | 2х2 – 2 – 3х + 1 – 8 = 0; 2х2 – 3х – 9 = 0; D = 9 + 72 = 81; х1 = = –1,5; х2 = = 3. О т в е т: –1,5; 3. |
2. х4 – 19х2 + 48 = 0.
Пусть х2 = t, тогда получим:
t2 – 19t + 48 = 0;
D = 361 – 192 = 169;
t1 = = 3, t2 = = 16.
В е р н е м с я к з а м е н е:
| х2 = 3; или х = ± . | х2 = 16; х = ±4. |
О т в е т: –4; – ; ; 4.
| 3. а) 2х2 – 13х + 6 < 0; у = 2х2 – 13х + 6. Ветви параболы направлены вверх. 2х2 – 13х + 6 = 0; D = 169 – 48 = 121; х1 = , х2 = = 6. |  |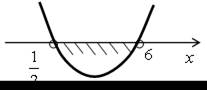
О т в е т:
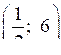.| б) х2 – 9 > 0; у = х2 – 9. Ветви параболы направлены вверх. х2 – 9 = 0; х2 = 9; х = ±3. |  |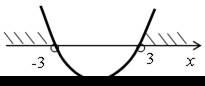
О т в е т: (–∞; –3) (3; +∞).
| в) 3х2 – 6х + 32 > 0; у =3х2 – 6х + 32. Ветви параболы направлены вверх. 3х2 – 6х + 32 = 0; D = 9 – 96 = –87 < 0. Парабола не пересекает ось х. |  |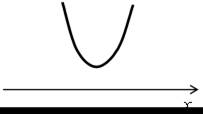
О т в е т: (–∞; +∞).
| 4. а) (х + 8) (х – 4) > 0; | б) < 0; | |
| х = –8; 4 – нули функции у = (х + 8) (х – 4). | (х – 5) (х + 7) < 0; х = –7; 5 – нули функции у = (х – 5) (х + 7). | |
 |  | |
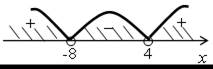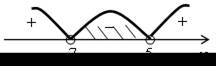| О т в е т: (–∞;–8) (4; +∞). | О т в е т: (–7; 5). | |
| 5. 3х2 + tх + 3 = 0; D = t2 – 36. Уравнение имеет два корня, если D > 0, t2 – 36 > 0; t2 (–∞;–6) (6; +∞). О т в е т: (–∞;–6) (6; +∞). |  | |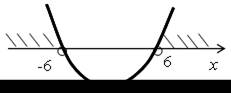
| | | |
6.*
+ 4 = 0.Пусть = t, тогда получим:
t + + 4 = 0;
t2 + 4t + 3 = 0;
t1 = –1, t2 = –3.
В е р н е м с я к з а м е н е:
| = –1; или х2 + 2х – 5 = 0; D1 = 1 + 5 = 6; х1, 2 = –1 ± . | = –3; х2 + 4х – 5 = 0; х1 = 1, х2 = –5. |
О т в е т: –5; 1; –1 ± .
В а р и а н т 2
| 1. а) х3 – 25х = 0; | | б)  = 1; |
| х (х2 – 25) = 0; | | 2(х2 + 6) – (8 – х) = 1 · 10; |
| х = 0 или О т в е т: –5; 0; 5. | х2 – 25 = 0; х2 = 25; х = ±5. | 2х2 + 12 – 8 + х – 10 = 0; 2х2 + х – 6 = 0; D = 1 + 48 = 49; х1 = = –2; х2 = = 1,5. О т в е т: –2; 1,5. |