ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 123
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= –а. Имеем:
х1 + х2 < 0, если –а < 0, то есть а > 0.
О т в е т: (–10; 10) (10; +∞).
3. При каком значении т сумма квадратов корней уравнения х2 +
+ (2 – т) х – т – 3 = 0 минимальна?
Р е ш е н и е
Данное уравнение должно иметь два корня, то есть дискриминант должен быть положительным:
D = (2 – т)2 + 4 (т + 3) = 4 – 4т + т2 + 4т + 12 = т2 + 16.
Выражение т2 + 16 положительно при любом значении т, то есть данное уравнение имеет два корня: х1 и х2. По условию сумма х1 + х2 должна быть минимальна.
Справедливо следующее равенство:
х12+ х22 = (х1 + х2)2 – 2х1 · х2.
По теореме Виета, х1 + х2 = т – 2, х1 · х2 = –т – 3.
Подставим полученные выражения в это равенство:
х12+ х22 = (т – 2)2 + 2(т + 3) = т2 – 4т + 4 + 2т + 6 = т2 – 2т + 10.
Выделим квадрат двучлена из квадратного трехчлена т2 – 2т + 10:
т2 – 2т + 10 = (т – 1)2 + 9.
Таким образом, имеем:
х12+ х22 = (т – 1)2 + 9.
Выражение (т – 1)2 + 9 принимает наименьшее значение при т = 1.
О т в е т: т = 1.
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какое наибольшее количество корней может иметь целое уравнение пятой степени?
– Какие существуют методы решения целых уравнений? Опишите каждый из них.
– Как решаются биквадратные уравнения? Сколько корней они могут иметь? Опишите все возможные случаи.
Домашнее задание:
1. № 358 (г, е), № 284 (б), № 274 (б).
2. Решите уравнение:
а) (х – 2)2 (х2 – 4х + 3) = 12;
б) х (х + 1) (х + 2) (х + 3) = 120.
Д о п о л н и те л ь н о: Докажите, что число 1 является корнем уравнения (2х2 – 4х + 3) (х2 – 2х + 2) = 1 и других корней у этого уравнения нет.
У р о к 28 Дата:
РЕШЕНИЕ ДРОБНО-РАЦИОНАЛЬНЫХ УРАВНЕНИЙ
ПО АЛГОРИТМУ
Цели: продолжить формирование умения решать дробно-рациональные уравнения, используя алгоритм, известный учащимся из курса 8 класса.
Ход урока
I. Организационный момент.
II. Устная работа.
Верно ли, что выражение
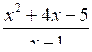обращается в нуль:а) при х = 2;
б) при х = –5;
в) при х = 1.
III. Объяснение нового материала.
В 8 классе учащиеся уже изучали данную тему. Сейчас необходимо расширить их знания. Отличия дробно-рациональных уравнений, изучаемых в 9 классе, состоят в следующем:
1) получаемое в процессе решения целое уравнение имеет степень, большую двух;
2) некоторые дробно-рациональные уравнения возможно решить, только используя метод введения новой переменной.
На этом уроке целесообразно актуализировать знания учащихся о решении дробно-рациональных уравнений по алгоритму. Вопрос о других приемах и методах решения дробно-рациональных уравнений лучше рассмотреть на следующем уроке.
Объяснение материала проводится в несколько э т а п о в.
1. И з у ч е н и е п о н я т и я дробно-рационального уравнения. Усвоение данного понятия проверяется при решении упражнения на распознавание этого вида уравнений.
З а д а н и е. Какие из следующих уравнений являются дробно-рациональными? Ответ объясните.
а) ; г) ;
б) ; д)
;в)
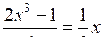; е) .2. В ы в о д а л г о р и т м а решения дробно-рациональных уравнений. Алгоритм приведен на с. 78 учебника. Желательно, чтобы учащиеся занесли его в тетрадь.
3. Р а с с м о т р е н и е п р и м е р о в решения дробно-рациональных уравнений по изученному алгоритму (пример 1 и пример 3 из учебника).
IV. Формирование умений и навыков.
Упражнения:
1. № 288 (а, в), № 289 (а).
2. № 290 (а), № 292 (б).
3. № 291 (в).
Р е ш е н и е
;
;
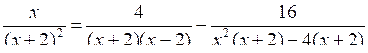
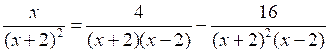;х (х – 2) = 4 (х + 2) – 16;
х2 – 2х – 4х – 8 + 16 = 0;
х2 – 6х + 8 = 0;
х1 = 2, х2 = 4;
х1 = 2 – не является корнем уравнения.
О т в е т: 4.
4. № 296 (а).
Р е ш е н и е
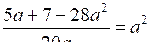;5а + 7 – 28а2 = 20а3;
5а + 7 – 4а2 (7 + 5а) = 0;
(5а + 7) (1 – 4а2) = 0;
| 5а + 7 = 0; или 5а = –7; а = –1,4. | 1 – 4а2 = 0; а2 = ; а = ± . |
О т в е т: –1,4; ±0,5.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какие уравнения называются дробно-рациональными?
– Являются ли следующие уравнения дробно-рациональными:
?– Опишите алгоритм решения дробно-рациональных уравнений.
Домашнее задание: № 289 (б), № 290 (б), № 291 (б), № 295 (б).
У р о к 29 Дата:
ИСПОЛЬЗОВАНИЕ РАЗЛИЧНЫХ ПРИЕМОВ И МЕТОДОВ
ПРИ РЕШЕНИИ ДРОБНО-РАЦИОНАЛЬНЫХ УРАВНЕНИЙ
Цели: продолжить формирование умения решать дробно-рациональные уравнения, используя при этом различные приемы и методы.
Ход урока
I. Организационный момент.
II. Устная работа.
Какие из чисел –1; 0; 2; 3 являются корнями уравнения:
а) = 0; б) = 0.
III. Объяснение нового материала.
1. Сначала необходимо актуализировать знания учащихся, попросив их рассказать алгоритм решения дробно-рациональных уравнений. После этого предложить учащимся использовать этот алгоритм при решении уравнения.
(пример 2 из учебника).Далее делается в ы в о д, что решение данного уравнения по алгоритму является громоздким, поэтому целесообразно применить ряд преобразований.
2. Рассмотреть пример 4 из учебника. Здесь возникает такая же ситуация: решение данного дробно-рационального уравнения приводит к целому уравнению четвертой степени, корни которого известными методами найти очень сложно. Зато после введения новой переменной полученное уравнение решается довольно просто.
3. На основании рассмотренных примеров делаются следующие
в ы в о д ы:
1) Не всякое дробно-рациональное уравнение целесообразно решать по алгоритму.
2) Довольно эффективным методом решения дробно-рациональных уравнений является метод введения новой переменной.
IV. Формирование умений и навыков.
Упражнения:
1. № 293 (а), № 294 (а).
2. № 297 (а, б), № 298 (б).
В классе с высоким уровнем подготовки можно решить еще несколько дробно-рациональных уравнений.
3. № 299 (а).
Р е ш е н и е
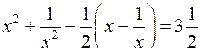.С д е л а е м з а м е н у: , тогда
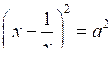
Получим уравнение:
;
;2а2 – а – 3 = 0;
а1 = –1, а2 = .
В е р н е м с я к з а м е н е:
| ; или х2 + х – 1 = 0; D = 1 + 4 = 5; х1, 2 = . | ; 2х2 – 3х – 2 = 0; D = 9 + 16 = 25; х1 = = 2; х2 = . |
О т в е т:
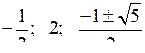.4.
= –1,5.Р е ш е н и е
Проверим, что х ≠ 0, и разделим числитель и знаменатель каждой дроби на х:
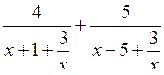= –1,5.С д е л а е м з а м е н у: . Получим:
;8 (а – 5) + 10 (а + 1) + 3 (а + 1) (а – 5) = 0;
8а – 40 + 10а + 10 + 3а2 – 15а + 3а – 15 = 0;
3а2 + 6а – 45 = 0;
а2 + 2а – 15 = 0;
а1 = –5, а2 = 3.
В е р н е м с я к з а м е н е:
| ; или х2 + 5х + 3 = 0; D = 25 – 12 = 13; х1, 2 = 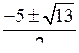 . | ; х2 – 3х + 3 = 0; D = 9 – 12 = –3. Решений нет. |
О т в е т:
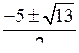.5. = 3.
Р е ш е н и е
Вычтем и прибавим к выражению, стоящему в левой части уравнения, выражение , чтобы получить полный квадрат:
;
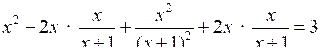