ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 120
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2. х4 – 4х2 – 45 = 0.
Пусть х2 = t, тогда получим:
t2 – 4t – 45 = 0;
t1 = –5, t2 = 9.
В е р н е м с я к з а м е н е:
| х2 = –5 . или Нет решений. | х2 = 9; х = ±3. |
О т в е т: ±3.
| 3. а) 2х2 – х – 15 > 0; у = 2х2 – х – 15 > 0. Ветви параболы направлены вверх. 2х2 – х – 15 = 0; D = 1 + 120 = 121; x1 = –2,5, x2 = = 3. | 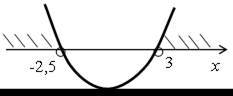 |
О т в е т: (–∞;–2,5) (3; +∞).
| б) х2 – 16 < 0; у = х2 – 16. Ветви параболы направлены вверх. х2 – 16 = 0; х2 = 16; х = ±4. | 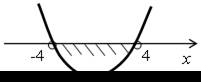 |
О т в е т: (–4; 4).
| в) х2 + 12х + 80 < 0; у = х2 + 12х + 80 < 0. Ветви параболы направлены вверх. х2 + 12х + 80 = 0; D = 36 – 80 = –44 < 0. Парабола не пересекает ось х. О т в е т: нет решений. | 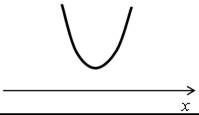 | ||
| 4. а) (х + 11) (х –9) < 0; | б) > 0; | ||
| х = –11; 9 – нули функции у = (х + 11) (х – 9). | (х + 3) (х – 8) > 0; х = –3; 8 – нули функции у = (х + 3) (х – 8). | ||
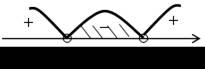 | 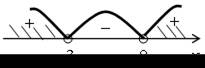 | ||
| О т в е т: (–11; 9). | О т в е т: (–∞;–3) (8; +∞). | ||
| 5. 2х2 + tх + 8 = 0; D = t2 – 64. Уравнение не имеет корней, если D < 0, t2 – 64 < 0; t = ±8. О т в е т: (–8; 8). | 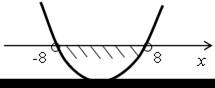 | ||
| | | | |
6.* = 3.
Пусть = t, тогда получим:
t – = 3;
t2 – 3t – 10 = 0;
t1 = –2, t2 = 5.
В е р н е м с я к з а м е н е:
| = –2 ; или х2 + 2х – 14 = 0; D1 = 1 + 14 = 15; х1, 2 = –1 ± . | = 5; х2 – 5х – 14 = 0; х1 = –2, х2 = 7. |
О т в е т: –2; 7; –1 ± .
В а р и а н т 3
| 1. а) х3 – 36х = 0; | | б)  = 1; = 1; |
| х (х2 – 36) = 0; | | 2(х2 – 4) – (5х – 2) = 1 · 6; |
| х = 0 или О т в е т: –6; 0; 6. | х2 – 36 = 0; х2 = 36; х = ±6. | 2х2 – 8 – 5х + 2 – 6 = 0; 2х2 – 5х – 12 = 0; D = 25 + 96 = 121; х1 = = –1,5; х2 = = 4. О т в е т: –1,5; 4. |
2. х4 – 13х2 + 36 = 0.
Пусть х2 = t, тогда получим:
t2 – 13t + 36 = 0;
t1 = 4, t2 = 9.
В е р н е м с я к з а м е н е:
| х2 = 4; или х = ±2. | х2 = 9; х = ±3. |
О т в е т: –3; –2; 2; 3.
| 3. а) 2х2 + 5х – 7 < 0; у = 2х2 + 5х – 7. Ветви параболы направлены вверх. 2х2 + 5х – 7 = 0; D = 25 + 56 = 81; x1 = = –3,5, x2 = = 1. | 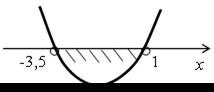 |
О т в е т: (–3,5; 1).
| б) х2 – 25 > 0; у = х2 – 25. Ветви параболы направлены вверх. х2 – 25 = 0; х2 = 25; х = ±5. | 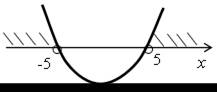 |
О т в е т: (–∞; –5) (5; +∞).
| в) 5х2 – 4х + 21 > 0; у = 5х2 – 4х + 21. Ветви параболы направлены вверх. 5х2 – 4х + 21 = 0; D = 4 – 105 = –101 < 0. Парабола не пересекает ось х. | 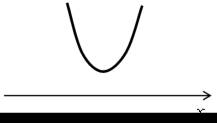 |
О т в е т: (–∞; +∞).
| 4. а) (х + 9) (х – 5) > 0; | б) < 0; | |
| х = –9; 5 – нули функции у = (х + 9) (х – 5). | (х – 3) (х + 6) < 0; х = –6; 3 – нули функции у = (х – 3) (х + 6). | |
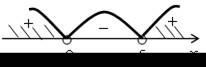 | 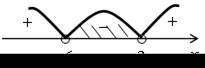 | |
| О т в е т: (–∞;–9) (5; +∞). | О т в е т: (–6; 3). | |
| 5. 2х2 + tх + 2 = 0; D = t2 – 16. Уравнение имеет два корня, если D > 0, t2 – 16 > 0; t = ±4. О т в е т: (–∞;–4) (4; +∞). | 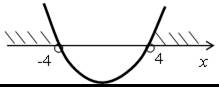 | |
| | | |
6.* = 2;
= 2.
Пусть х2 + 6х + 5 = t, тогда получим:
= 2;
12 (t + 3) + 15t = 2t (t + 3);
12t + 36 + 15t = 2t2 + 6t;
2t2 – 21t – 36 = 0;
D = 441 + 288 = 729;
t1 = = 12, t2 = = .
В е р н е м с я к з а м е н е:
| х2 + 6х + 5 = 12; или | х2 + 6х + 5 = ; |
| х2 + 6х – 7 = 0; х1 = 1, х2 = –7. | 2х2 + 12х + 13 = 0; D1 = 36 – 26 = 10; х1, 2 = . |
О т в е т: –7; 1; .
В а р и а н т 4
| 1. а) х3 – 49х = 0; | | б)  = 2; = 2; |
| х (х2 – 49) = 0; | | 2(х2 + 3) – (17 – 3х) = 2 · 8; |
| х = 0 или О т в е т: –7; 0; 7. | х2 – 49 = 0; х2 = 49; х = ±7. | 2х2 + 6 – 17 + 3х = 16; 2х2 + 3х – 27 = 0; D = 9 + 216 = 225; х1 = = 3; х2 = = –4,5. О т в е т: –4,5; 3. |
2. х4 – 17х2 + 16 = 0.
Пусть х2 = t, тогда получим:
t2 – 17t + 16 = 0;
t1 = 1, t2 = 16.
В е р н е м с я к з а м е н е:
| х2 = 1; или х = ±1. | х2 = 16; х = ±4. |
О т в е т: –4; –1; 1; 4.
| 3. а) 5х2 + 3х – 8 > 0; у = 5х2 + 3х – 8. Ветви параболы направлены вверх. 5х2 + 3х – 8 = 0; D = 9 + 160 = 169; x1 = = 1, x2 = = –1,6. | 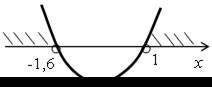 |
О т в е т: (–∞;–1,6) (1; +∞).
| б) х2 – 49 < 0; у = х2 – 49. Ветви параболы направлены вверх. х2 – 49 = 0; х2 = 49; х = ±7. | 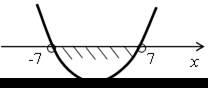 |
О т в е т: (–7; 7).
| в) 4х2 – 2х + 13 < 0; у = 4х2 – 2х + 13. Ветви параболы направлены вверх. 4х2 – 2х + 13 = 0; D = 1 – 52 = –51 < 0. Парабола не пересекает ось х. | 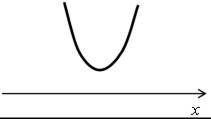 |
О т в е т: нет решений.
| 4. а) (х + 12) (х –7) < 0; | б) > 0; | |
| х = –12; 7 – нули функции у = (х + 12) (х – 7). | (х + 5) (х – 10) > 0; х = –5; 10 – нули функции у = (х + 5) (х – 10). | |
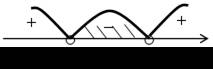 | 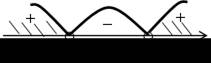 | |
| О т в е т: (–12; 7). | О т в е т: (–∞;–5) (10; +∞). | |
| 5. 25х2 + tх + 1 = 0; D = t2 – 100. Уравнение не имеет корней, если D < 0, t2 – 100 < 0, t = ±10. О т в е т: (–10; 10). | 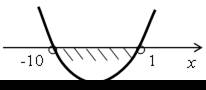 | |
| | | |