ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 124
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1. № 330, № 332.
2. Решите неравенство:
а) (2 – х) (6 – х)
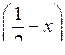< 0;б) –х
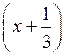(5 – х) ≥ 0;в) –(х – 4) (1 + х)
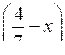< 0.2-я г р у п п а.
1. № 334.
2. № 336 (а, б).
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Опишите суть метода интервалов решения неравенств.
– Как метод интервалов может быть использован при решении дробно-рациональных неравенств?
– В чем состоят особенности решения методом интервалов строгих и нестрогих дробно-рациональных неравенств?
Домашнее задание: № 331, № 333, № 335, № 336 (в, г).
У р о к 35 Дата:
ПРИМЕНЕНИЕ МЕТОДА ИНТЕРВАЛОВ
ПРИ РЕШЕНИИ БОЛЕЕ СЛОЖНЫХ НЕРАВЕНСТВ
Цели: продолжить формирование умения решать неравенства методом интервалов; рассмотреть, как может быть применен метод при решении более сложных неравенств.
Ход урока
I. Организационный момент.
II. Устная работа.
Решите неравенство:
а) (х + 1) (х – 3) > 0; в)
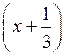(х – 10) < 0;б) (х – 5) (х – 2) ≤ 0; г) (х – 4) ≥ 0.
III. Проверочная работа.
В а р и а н т 1
1. Решите неравенство:
а) < 0; б) ≥ 0.
2. Найдите область определения функции:
а) y = ; б) y = .
В а р и а н т 2
1. Решите неравенство:
а) > 0; б) ≤ 0 .
2. Найдите область определения функции:
а) y = ; б) y =
.IV. Формирование умений и навыков.
Все задания, выполняемые на уроке, можно разбить на две группы. В первую группу войдут дробные неравенства и неравенства, которые до применения метода интервалов предварительно нужно преобразовать, разложив на множители их левую часть. Во вторую группу войдут более сложные неравенства. Чтобы применить к ним метод интервалов, необходимо сначала перейти к равносильной системе.
Вторую группу заданий следует решать в классе с высоким уровнем подготовки.
Упражнения:
1-я г р у п п а.
1. № 338.
Р е ш е н и е
в) ≥ 2.
Перенесем число 2 в левую часть неравенства и приведем его к виду ≥ 0:
– 2 ≥ 0;
≥ 0;
≥ 0;
≤ 0;
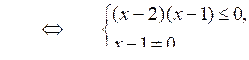
Решая эту систему, получим, что х (1; 2].
О т в е т: (1; 2].
2. Решите неравенство, разложив его левую часть на множители:
а) (4 – х2)
< 0; г) х3 – 5х + 6х £ 0;б) х3 – 16х ³ 0; д) (х2 + 3х) < 0;
в) (х2 – 25)
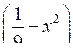> 0; е) 8х3 + 12х2 – 2х – 3 > 0.2-я г р у п п а.
Решите неравенство:
а) (3х2 + 5) (х + 7)
> 0.Р е ш е н и е
Поскольку выражение 3х2 + 5 положительно при всех значениях х, то обе части неравенства можно разделить на него. Получим неравенство:
(х + 7)
> 0 или (х + 7)
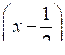< 0.Решая его, находим, что х
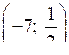.О т в е т:
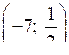.б) (х + 2)2 (х – 6) < 0.
Р е ш е н и е
Выражение (х + 2)2 неотрицательно при всех значениях х, поэтому данное неравенство равносильно системе:
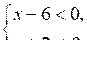
Решая систему, находим, что х (–∞; –2) (–2; 6).
О т в е т: (–∞; –2) (–2; 6).
в) (х –3)2 (х – 10) ≥ 0
Р е ш е н и е
Выражение (х –3)2 неотрицательно при всех значениях х, и если оно равно нулю, то и произведение (х –3)2 (х – 10) равно нулю. Поэтому данное равносильно системе:
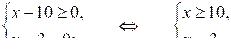
Получаем, что х {3} [10; +∞).
О т в е т: {3} [10; +∞).
г)
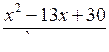< 0.Р е ш е н и е
Разложим на множители числитель и знаменатель дроби:
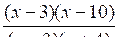< 0.Данное неравенство равносильно системе:
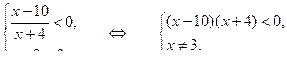
Решая систему, находим, что х (–4; 3) (3; 10).
О т в е т: (–4; 3) (3; 10).
д) ≤ 0.
Р е ш е н и е
Разложим на множители числитель и знаменатель дроби:
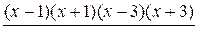≤ 0.Это неравенство равносильно системе:
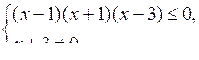
Решая его находим, что х (–∞; –3) (–3; –1] [1; 3].
О т в е т: (–∞; –3) (–3; –1] [1; 3].
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– В чем состоит метод интервалов решения неравенств?
– Любое ли неравенство можно решить методом интервалов?
– Как применяется метод интервалов к решению дробных неравенств?
– Как решается неравенство, содержащее целое выражение выше второй степени?
Домашнее задание: № 389, № 394.
Д о п о л н и т е л ь н о: № 390.
В а р и а н т 1
1. Решите неравенство:
а) < 0; б) ≥ 0.
2. Найдите область определения функции:
а) y = ; б) y = .
В а р и а н т 2
1. Решите неравенство:
а) > 0; б) ≤ 0 .
2. Найдите область определения функции:
а) y = ; б) y =
.В а р и а н т 1
1. Решите неравенство:
а) < 0; б) ≥ 0.
2. Найдите область определения функции:
а) y = ; б) y = .
В а р и а н т 2
1. Решите неравенство:
а) > 0; б) ≤ 0 .
2. Найдите область определения функции:
а) y = ; б) y =
.
У р о к 36 Дата:
ИТОГОВЫЙ УРОК ПО ТЕМЕ
«УРАВНЕНИЯ И НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ»
Цели: обобщить и систематизировать знания учащихся по теме; подготовить учащихся к написанию контрольной работы.
Ход урока
I. Организационный момент.
II. Актуализация знаний.
Необходимо обобщить и систематизировать знания учащихся о видах уравнений и неравенств и методах их решения. Для этого нужно со-ставить классификацию уравнений и неравенств, изобразив ее на плакате или на доске. Учащиеся должны занести в тетрадь соответствующие схемы.
| | | | |||||||
| |  | |  | | |||||
| |  | ||||||||
 |  |  | | | | ||||
| 1-й степени (линейные) Р е ш е н и е: привести к виду ах = b х = | 2-й степени (квадратные) Р е ш е н и е: D = b2 – 4ac x1, 2 = | Выше 2-й степени | Решаемые по алгоритму | | Решаемые методом замены | ||||
  | |||||||||
| Решаемые методом замены | Решаемые разложением на множители | | | ||||||
| |  | | |||||||
| |  | | | | |||||
| | | ||||||||
| | | | | ||||||
| 1-й степени (линейные) Р е ш е н и е: привести к виду ах < > b | 2-й степени (квадратные) Р е ш е н и е: графически с помощью параболы | Выше 2-й степени Р е ш е н и е: метод интервалов | Решаются методом интервалов | ||||||
| | | | | | | | | ||