ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1014
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ГЛАВА 3. УРАВНЕНИЯ И НЕРАВЕНСТВА С ДВУМЯ ПЕРЕМЕННЫМИ
У р о к 38 Дата:
ПОНЯТИЕ УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ
Цели: ввести понятие уравнения с двумя переменными, его степени, корней и графика; формировать умение использовать данные понятия
Ход урока
I. Организационный момент.
II. Устная работа.
1. Назовите степень многочлена:
а) 3х7 + 2х3 – х + 1; в) ab3 – a2b + a3b4;
б) 3х5 + 2х3у3 – у2; г) 2m4n2+ 3m3n4 – 6n5.
2. Подберите три пары чисел a и b таких, чтобы выполнялось равенство 2a – b = 5.
III. Объяснение нового материала.
Объяснение проводить согласно пункту учебника, включая устные задания, проверяющие степень усвоения материала.
1. В в е д е н и е п о н я т и я уравнения с двумя переменными.
З а д а н и е. Какие из следующих уравнений являются уравнениями с двумя переменными:
а) 2х3 + = 5х2; г) х2 + 2у + 7 = z;
б) 2х + 3у3 = 7; д) + 5 = х – у;
| в) ab + 3а = b4; | е) 2n + 4m2 = ? |
2. Р е ш е н и е у р а в н е н и я с двумя переменными.
З а д а н и е. Проверить, какие из следующих пар являются решениями уравнения х + 2у = 1.
а) ; б) (2; –1); в) (3; –1); г) .
3. С т е п е н ь у р а в н е н и я с двумя переменными.
З а д а н и е № 397.
4. Г р а ф и к у р а в н е н и я с двумя переменными.
Необходимо актуализировать знания учащихся о графиках известных им элементарных функций. Рассмотреть вопрос о том, как может быть построен график уравнения с двумя переменными.
Вопрос о графике уравнения х2 +
у2 = r2 целесообразно рассмотреть на следующем уроке.
IV. Формирование умений и навыков.
Основное внимание на этом уроке следует уделить понятию уравнения с двумя переменными и нахождению его корней подбором. На формирование этого умения направлена первая группа заданий. Во вторую группу войдут задания, связанные с графиком уравнений с двумя переменными. Более сложные задания на построение графиков лучше рассмотреть на следующем уроке.
Упражнения:
1-я г р у п п а.
1. № 395.
2. Найдите несколько решений уравнения:
а) 2х + у = 5; в) х2 – ху = 1;
б) х – у = ; г) (х + 1) (у – 3) = 12.
2-я г р у п п а.
1. № 399 (а, в, д, ж), № 402 (а, б).
2. № 400.
В классе с высоким уровнем подготовки можно дополнительно выполнить № 411.
Р е ш е н и е
а) ху = 2.
Выразим переменную х через у: х = .
Чтобы х было целым числом, выражение должно принимать целые значения, то есть число 2 должно нацело делиться на у. Это условие будет выполнено, если у = ±1 и у = ±2. В этом случае х = ±2 и х = ±1 соответственно.
О т в е т: (2; 1), (–2; –1), (1; 2), (–1; –2).
б) х2 – у2 = 3.
Преобразуем выражение х2 – у2 по формуле разности квадратов:
(х – у) (х + у) = 3.
Если х и у – целые числа, то х – у и х + у – целые числа. Целые числа дают в произведении 3 в четырех случаях: 1 · 3; 3 · 1; –1 · (–3); –3 · (–1). Получим четыре системы уравнений:
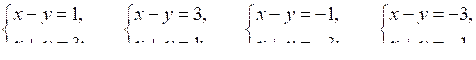
Решая эти системы, находим нужные пары чисел.
О т в е т: (2; 1), (2; –1), (–2; –1), (–2; 1).
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какое уравнение называется уравнением с двумя переменными?
– Что называется степенью уравнения с двумя переменными?
– Что называется решением уравнения с двумя переменными?
– Сколько может иметь решений уравнение с двумя переменными?
– Графики каких уравнений с двумя переменными вы умеете строить?
Домашнее задание: № 396, № 399 (б, г, е, з), № 401.
У р о к 39 Дата:
УРАВНЕНИЕ ОКРУЖНОСТИ
Цели: изучить уравнение окружности; формировать умение составлять это уравнение.
Ход урока
I. Организационный момент.
II. Устная работа.
Является ли пара чисел (2; –1) решением уравнения:
а) х + 3у = 1; в) х2 – у2 = ;
б) – 2у = 3; г) 2ху + у = –3.
III. Проверочная работа.
В а р и а н т 1
1. Найдите два каких-нибудь решения уравнения:
а) 2х – у = 3; б)
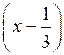(у + 2) = 0.2. Постройте график уравнения:
а) – у = 1; б) (х + 1) (у – 3) = 0.
В а р и а н т 2
1. Найдите два каких-нибудь решения уравнения:
а) х2 + у = 7; б) (х – 1) = 0.
2. Постройте график уравнения:
а) 2х + у = ; б) (х – 2) (у + 1) = 0.
IV. Объяснение нового материала.
Сначала следует актуализировать знания учащихся об известных им графиках уравнений с двумя переменными. Затем разобрать, что является графиком уравнения х2 + у2 = r2, и вывести общее уравнение окружности с центром в точке (a; b) и радиусом r:
(х – а)2 + (у – b)2 = r2.
V. Формирование умений и навыков.
Задания можно разбить на две группы. Сначала учащиеся по данному уравнению окружности строят ее, а затем выполняют задания на составление уравнения окружности.
Упражнения:
1-я г р у п п а.
1. № 403 (устно).
2. Постройте график уравнения:
а) х2 + у2 = 4;
б) (х – 1)2 + у2 = 9;
в) (х + 2)2 + (у – 3)2 = 1.
2-я г р у п п а.
1. № 404 (а, б), № 405 (а, б).
2. № 407.
3. № 410.
В классе с высоким уровнем подготовки можно выполнить несколько дополнительных заданий.
1. № 406.
Р е ш е н и е
х2 + у2 – 6 (х – у) = 7.
Для того чтобы доказать, что графиком этого уравнения является окружность, его нужно привести к виду
(х – а)2 + (у – b)2 = r2.
Выполним ряд преобразований:
х2 + у2 – 6х + 6у = 7;
х2 – 6
х + 9 – 9 + у2 + 6у + 9 – 9 = 7;
(х – 3)2 – 9 + (у + 3)2 – 9 = 7;
(х – 3)2 + (у + 3)2 = 25.
Таким образом, графиком данного уравнения является окружность с центром в точке (3; –3) и радиусом 5.
2. № 409.
Р е ш е н и е
Центром окружности (х – 5)2 + (у – 7)2 = r2 является точка с координатами (5; 7), то есть центр этой окружности находится в первой координатной четверти на расстоянии 5 от оси у и 7 – от оси х.
Чтобы данная окружность касалась оси х, ее радиус должен совпадать с расстоянием между центром и осью х, то есть r = 7. А чтобы окружность касалась оси у, ее радиус должен совпадать с расстоянием между центром и осью у, то есть r = 5.
VI. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется решением уравнения с двумя переменными?
– Сколько решений имеет уравнение с двумя переменными?
– Что является графиком уравнения х2 + у2 = r2?
– Назовите координаты центра окружности и ее радиус, если она задана уравнением (х + 1)2 + (у – 5)2 = 49.
Домашнее задание: № 402 (в, г), № 404 (в), № 405 (в).
Д о п о л н и т е л ь н о: № 408.
У р о к 40 Дата:
СУТЬ ГРАФИЧЕСКОГО СПОСОБА РЕШЕНИЯ
СИСТЕМ УРАВНЕНИЙ
Цели: познакомить учащихся с системами уравнений, в которых хотя бы одно из них является уравнением второй степени; формировать умение решать такие системы графически.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Является ли пара чисел (–1; 3) решением системы уравнений:
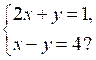
| 2. На рисунке изображены графики функций у = 2х + 4 и у = –х + 1. Решите систему уравнений:  |  |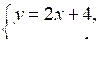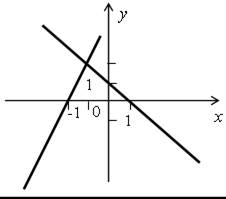
III. Объяснение нового материала.
1. Сначала необходимо актуализировать знания учащихся по следующим вопросам:
– понятие системы уравнений;
– решение системы уравнений;
– способы решения систем линейных уравнений.
2. Показать учащимся, что в некоторых ситуациях необходимо уметь решать не только системы линейных уравнений, но и системы, в которых хотя бы одно из уравнений имеет вторую степень.
3. Продемонстрировать графический способ решения систем уравнений (пример из учебника).
IV. Формирование умений и навыков.
Задания лучше разбить на две группы. Первая группа подготавливает учащихся к применению графического способа решения систем уравнений. А во вторую группу будут входить задания на непосредственное решение систем уравнений графически.
Упражнения:
1-я г р у п п а.
1. № 415.
| 2. На рисунке изображены графики функций у = –х2 + 2 и у = . Решите систему уравнений:  |  |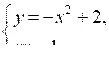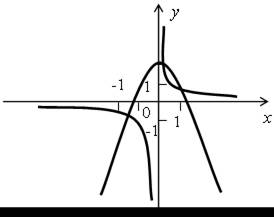
3. Постройте график функции у = х2 – 4. С помощью этого графика решите систему уравнений:
а)
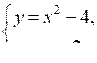б)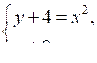 
2-я г р у п п а.
№ 416, № 417.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется решением системы уравнений?
– В чем состоит суть графического способа решения системы уравнений?
– Сколько решений имели системы уравнений, которые были рассмотрены на этом уроке?
– Может ли система уравнений не иметь решений?
Домашнее задание: № 417, № 523 (а, г, е).
У р о к 41 Дата:
РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ГРАФИЧЕСКИ
Цели: продолжить формирование умения решать графически системы уравнений; дать наглядные представления о возможном количестве решений систем уравнений.