ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1016
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Выразим из второго уравнения переменную у и подставим в первое уравнение:
2у = –3х – 1;
у = ;
х2 + х ∙ + 3 ∙ = 9;
2х2 – 3х2 – х + 9х + 3 = 18;
–х2 + 8х – 15 = 0;
х2 – 8х + 15 = 0;
x1 = 3 y1 = = 5;
x2 = 5 y2 = = –8.
О т в е т: (3; –5), (5; –8).
Сильным в учебе учащимся можно дополнительно дать карточки.
К а р т о ч к а № 1
1. Решите систему уравнений:
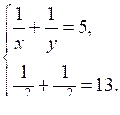
2. При каких значениях а система уравнений
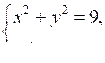имеет единственное решение?К а р т о ч к а № 2
1. Решите систему уравнений:
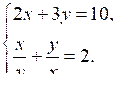
2. При каких значениях р система уравнений
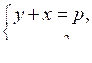не имеет решений?Р е ш е н и е заданий карточки № 1
1. При решении этой системы можно воспользоваться методом замены.
Пусть = n и = m. Получим систему:
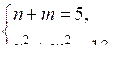
п = 5 – т;
(5 – т)2 + т2 = 13;
25 – 10т + т2 + т2 = 13;
2т2 – 10т + 12 = 0;
т2 – 5т + 6 = 0;
т1 = 2 п1 = 3;
т2 = 3 п2 = 2.
В е р н е м с я к з а м е н е:
= 3, то есть х = ; = 2, то есть у = ;
= 2, то есть х = ; = 3, то есть у = .
О т в е т: .
2. Выразим из второго уравнения системы переменную х и подставим в первое уравнение:
х = а – у;
(а – у)2 + у2 = 9;
а2 – 2ау + у2 + у2 = 9;
2у2 – 2ау + а2 – 9 = 0.
Чтобы система имела единственное решение, это уравнение должно иметь единственный корень, то есть дискриминант должен быть равен нулю.
D1 = а2 – 2 (а2 – 9) = 18 – а2;
18 – а2 = 0;
а2 = 18;
а = ± .
О т в е т: ± .
Р е ш е н и е заданий карточки № 2
1. Из первого уравнения выразим переменную х и подставим во второе уравнение системы:
x =
;
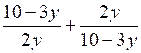= 2.Пусть
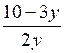= t, тогда получим уравнение:t + = 2;
t2 – 2t + 1 = 0;
t = 1.
В е р н е м с я к з а м е н е:
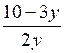= 1;10 – 3у = 2у;
5у = 10;
у = 2 х = = 2.
О т в е т: (2; 2).
2. Выразим из первого уравнения переменную у и подставим во второе уравнение системы:
у = р – х;
4 (р – х) = х2;
х2 + 4х – 4р = 0.
Чтобы система не имела решений, это уравнение не должно иметь корней, то есть дискриминант должен быть меньше нуля:
D1 = 4 + 4р;
4 + 4р < 0;
4р < –4;
р < –1.
О т в е т: (–∞; –1).
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется решением системы уравнений?
– Сколько решений может иметь система уравнений второй степени?
– В чем состоит способ подстановки решения систем уравнений второй степени?
Домашнее задание: № 434 (б, г), № 435 (б), № 437 (б), № 439,
№ 442 (а).
У р о к 44 Дата:
ИСПОЛЬЗОВАНИЕ СПОСОБА СЛОЖЕНИЯ
ПРИ РЕШЕНИИ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ
Цели: изучить способ сложения решения систем уравнений второй степени; формировать умение применять этот способ.
Ход урока
I. Организационный момент.
II. Проверочная работа.
В а р и а н т 1
1. Является ли пара чисел х = 6, у = –8 решением системы уравнений
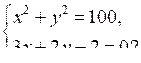
2. Решите систему уравнений:
а)
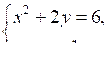б)
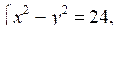
В а р и а н т 2
1. Является ли пара чисел х = 7, у = –6 решением системы уравнений:
2. Решите систему уравнений:
а)
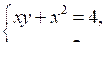б)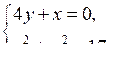 
III. Объяснение нового материала.
Сначала необходимо актуализировать знания учащихся о способе сложения при решении систем линейных уравнений. Предложить им решить данным способом систему, проговаривая все действия, которые они при этом совершают.
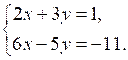
Умножим правую и левую части первого уравнения на –3. Получим систему:
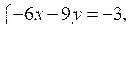
Сложим почленно левые и правые части уравнений полученной системы:
–14у = –14;
у = 1.
Подставим найденное значение переменной у в одно из уравнений исходной системы, например, в первое:
2х + 3 · 1 = 1;
2х = –2;
х = –1.
О т в е т: (–1; –1).
Затем сообщить учащимся, что способ сложения иногда можно применять и при решении систем уравнений второй степени. Показать это на конкретном примере:
Умножим правую и левую части первого уравнения на –2. Получим систему:
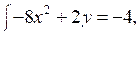
Сложим почленно левые и правые части уравнений полученной системы:
–8х2 + 3х = –5;
8х2 – 3х – 5 = 0;
х1 = 1, х2 = .
Подставим найденные значения переменной х во второе уравнение исходной системы:
| 3 · 1 – 2у = –1; 2у = 4; у = 2. |  |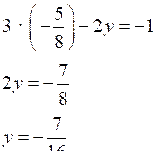
О т в е т: (1; 2), .
IV. Формирование умений и навыков.
1. Решите систему уравнений сначала способом подстановки, а затем способом сложения, сравните результаты.
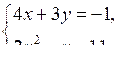
Какой способ в данном случае рациональнее?
2. Решите систему уравнений, используя способ сложения:
а)
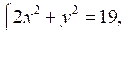б)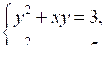 
Можно ли решить эти системы способом подстановки?
3. № 449 (а).
4. Решите систему уравнений:
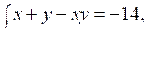
Р е ш е н и е
Сложим почленно левые и правые части уравнений данной системы. Получим уравнение:
2х + 2у = –12;
х + у = –6.
Данная система уравнений будет равносильна системе, составленной из полученного уравнения и любого уравнения исходной системы:
Эту систему уравнений можно решить способом подстановки:
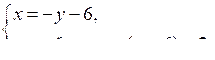
– 6 – у2 – 6у = 2;
у2 + 6у +8 = 0;
у1 = –2 х1 = 2 – 6 = –4;
у2 = –4 х2 = 4 – 6 = –2.
О т в е т: (–4; –2), (–2; –4).
Сильным в учебе учащимся можно предложить дополнительно решить № 534.
Р е ш е н и е
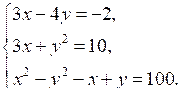
Чтобы данная система уравнений имела решение, нужно, чтобы решения системы, составленной из первых двух уравнений, являлись решениями третьего уравнения.
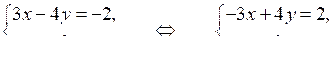
Сложим почленно левые и правые части уравнений данной системы. Получим уравнение:
у2 + 4у – 12 = 0;
у1 = 2, у2 = –6.
Подставим найденные значения переменной у в первое уравнение системы. Получим:
| 3х – 4 · 2 = –2; 3х = 6; х = 2. | 3х + 24 = –2; 3х = –26; х = . |
Подставляя полученное решение (2; 2) в третье уравнение исходной системы, убеждаемся, что она не имеет решений.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Опишите алгоритм решения систем уравнений второй степени способом сложения.
– Любую ли систему уравнений второй степени можно решить способом сложения?
Домашнее задание: № 445, № 448, № 449 (б).
У р ок 45 Дата:
РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ
РАЗЛИЧНЫМИ СПОСОБАМИ
Цели: обобщить и систематизировать знания учащихся о способах решения систем уравнений второй степени.
Ход урока
I. Организационный момент.
II. Устная работа.
Решите систему уравнений способом сложения:
а)
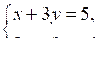б)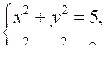 
III. Формирование умений и навыков.
Все задания можно разбить на две группы. В классе с невысоким уровнем подготовки задания второй группы решать не обязательно.
Упражнения:
1-я г р у п п а.
1. № 443 (а, в).
2. № 444.
3. № 447 (а).
Р е ш е н и е
Из второго уравнения выразим переменную х и подставим в первое уравнение системы:
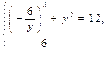
Пусть у2 = а, тогда получим уравнение:
+ а – 12 = 0;
а2 – 12а + 36 = 0;
(а – 6)2 = 0;
а = 6, то есть у2 = 6;
у = ± .
Тогда соответствующие значения х будут равны .
О т в е т: ( ; – ), (– ; ).
После решения этой системы предложить учащимся найти другой способ. Если они не догадаются, то помочь им.
Умножим обе части второго уравнения на 2 и сложим почленно левые и правые части уравнений полученной системы:
х2 + 2ху + у2 = 0;
(х