ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1015
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= 0;
при х ≠ 0, х ≠ 1 198х – 190х + 190 – 3х2 + 3х = 0;
3х2 – 11х – 190 = 0;
D = 112 – 4 · 3 · (–190) = 121 + 2280 = 2401;
х1 =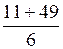
= 10;
х2 =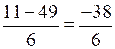
– не удовлетворяет условию задачи (х > 0).
10 (га) – отвели под пшеницу в прошлом году;
10 – 1= 9 (га) – в этом году.
О т в е т: 10 га; 9 га.
В а р и а н т IV
1.
.
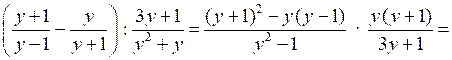
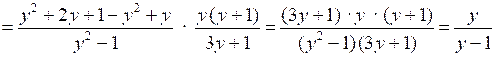О т в е т: .
2.
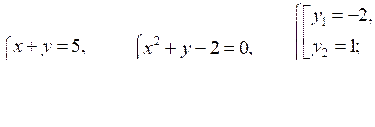
О т в е т: (7; –2), (4; 1).
3. х – 2,5 (2х – 1) > х – 1,5;
х – 5х + 2,5 > х – 1,5;
– 5х > –4;
х < ;
х < 0,8.
О т в е т: х < 0,8.
4.
;
.
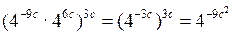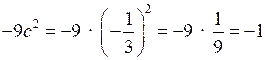
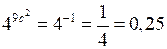О т в е т: 0,25.
5. у = х2 + 2х. Графиком является парабола, вершина в точке (х0; у0), где х0 = = –1; у0 = –1. Точки пересечения с осями координат находим из уравнения х2 + 2х = 0;
Функция принимает положительные значения, если х (–∞; –2)
(0; +∞).
6. Общее число книг 8 + 4 = 12. Исходами опыта являются все возможные сочетания из 5 книг (порядок значения не имеет).
Общее число исходов: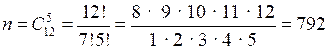
.
Событие А – «из выбранных книг – 3 приключенческих романа и 2 сборника стихотворений».
Количество благоприятных исходов:
.
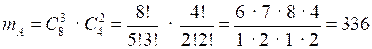Искомая вероятность: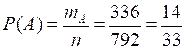
.
О т в е т: .
7. Пусть х км – расстояние между пунктами А и В, тогда (ч) – время, которое автобус должен был быть в пути. Половину пути автобус проехал за (ч), а вторую половину за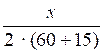
(ч). Зная, что он еще и простоял ч, но приехал в пункт В вовремя, составим уравнение:
;
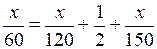75х + 4500 + 60х – 150х = 0;
15х = 4500;
х = 300.
О т в е т: 300 км.
У р о к 17 (101).
АНАЛИЗ ИТОГОВОЙ КОНТРОЛЬНОЙ РАБОТЫ
Цели: рассмотреть, проанализировать типичные ошибки, допущенные большинством учащихся; выполнить работу над ошибками.
Ход урока
I. Организационный момент.
II. Выполнение работы над ошибками.
Осуществляем поиск ошибок, анализируем, повторяем теоретический материал и решаем заново упражнения, в которых допущены ошибки.
III. Формирование умений и навыков.
Учащиеся, получившие отметку «отлично» или выполнившие работу над ошибками, приступают к решению заданий, соответствующих перечню контролируемых на государственной итоговой аттестации вопросов.
Задания представлены в двух частях. Часть I направлена на проверку достижения уровня базовой подготовки учащихся по алгебре. Часть II предназначена для дифференцированной проверки повышенного уровня алгебраической подготовки учащихся.
Сильные в учебе учащиеся могут решать только вторую часть.
Упражнения:
Ч а с т ь I
1. Вычислите: 4,5 + 2 · 5–2.
1) –45,5; 2) –15,5; 3) 4,58; 4) 4,42.
2. Премию в 26 тыс. р. было решено распределить между тремя рабочими в отношении 2 : 4 : 7. Сколько составляет наибольшая премия?
1) 8 тыс. р.; 2) 14 тыс. р.; 3) 16 тыс. р.; 4) 18 тыс. р.
3. Упростите выражение: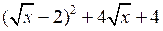
.
1) х + 8; 2) ; 3)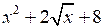
; 4) .
4. Разложите на множители: 81x6y4 – 0,36z2.
1) (9x3y2 – 0,6z)2;
2) (9x4y2 – 0,6z)2;
3) (9x3y2 – 0,6z) (9x3y2 + 0,6z);
4) (9x4y2 – 0,6z) (9x4y2 + 0,6z).
5. Найдите количество корней уравнения:
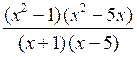= 0.
О т в е т: _______.
6. Решите неравенство: 2х – х2 < 0.
1) (0; 2); 3) (–∞; 0) (2; +∞);
2) (2; +∞); 4) (–∞; 2).
7. Решите систему уравнений: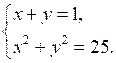
О т в е т: ______.
8. Арифметическая прогрессия задана формулой ап = 37,3 – 0,3п. Найдите номер наибольшего отрицательного члена прогрессии.
О т в е т: ______.
О т в е т ы:
Ч а с т ь II
1. Решить неравенство: х3 – х2 – 6х < 0.
Р е ш е н и е
х3 – х2 – 6х < 0;
х (х2 – х – 6) < 0;
х (х – 3) (х + 2) < 0.
(–∞; –2) (0; 3).
О т в е т: (–∞; –2) (0; 3).
2. Две машинистки, работая вместе, могут напечатать 22 страницы текста за 1 ч. Чтобы напечатать 120 страниц текста, первая машинистка потратит на 2 ч больше, чем вторая. За сколько часов первая машинистка сможет напечатать 300 страниц текста?
Р е ш е н и е
А н а л и з:
А = р · t
Пусть х с./ч – производительность первой машинистки, тогда (22 – х) с./ч – производительность второй машинистки. На печать 120 страниц первая машинистка затратит ч, а вторая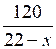
ч. Зная, что первая машинистка затратила на 2 ч больше, составим уравнение:
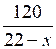– = 2;
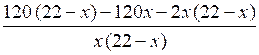= 0;
при х ≠ 0, х ≠ 22 2640 – 120х – 120х – 44х + 2х2 = 0;
х2 – 142х + 1320 = 0;
D1 = (71)2 – 1320 = 3721;
х1 = 71 + 61 = 132 – не удовлетворяет условию задачи (х < 22);
х2 = 71 – 61 = 10;
= 30 (ч) – затратит первая машинистка.
О т в е т: 30 ч.
3. Найдите сумму всех положительных трехзначных чисел, не делящихся на 13.
Р е ш е н и е
Количество трехзначных чисел равно 900 (100 ≤ х ≤ 999). Найдем сумму всех этих чисел и вычтем из нее сумму чисел, делящихся на 13.
1) (ап) – арифметическая прогрессия, где а1 = 100, ап = 999, d = 1.
.
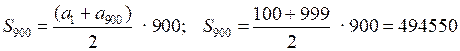2) (bn) – арифметическая прогрессия, b1 = 104, d = 13, bn ≤ 999.
bn = 104 + 13 (п – 1) = 91 + 13п;
91 + 13п ≤ 999;
13п ≤ 908;
п ≤ 69,8, п = 69;
;
.
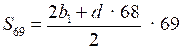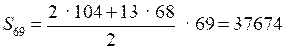3) 494550 – 37674 = 456876.
О т в е т: 456876.
4. Упростите выражение: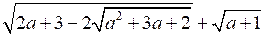
.
Р е ш е н и е
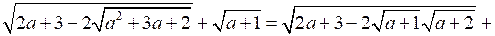
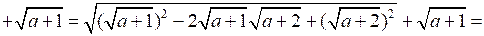
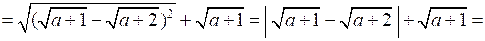
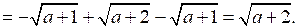
при х ≠ 0, х ≠ 1 198х – 190х + 190 – 3х2 + 3х = 0;
3х2 – 11х – 190 = 0;
D = 112 – 4 · 3 · (–190) = 121 + 2280 = 2401;
х1 =
= 10;х2 =
– не удовлетворяет условию задачи (х > 0).10 (га) – отвели под пшеницу в прошлом году;
10 – 1= 9 (га) – в этом году.
О т в е т: 10 га; 9 га.
В а р и а н т IV
1.
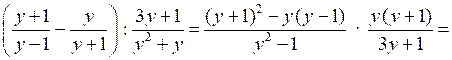
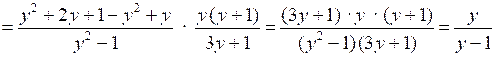.О т в е т: .
2.
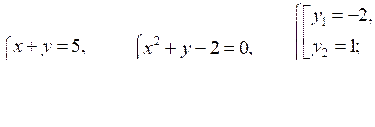
О т в е т: (7; –2), (4; 1).
3. х – 2,5 (2х – 1) > х – 1,5;
х – 5х + 2,5 > х – 1,5;
– 5х > –4;
х < ;
х < 0,8.
О т в е т: х < 0,8.
4.
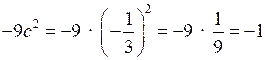
; .О т в е т: 0,25.
5. у = х2 + 2х. Графиком является парабола, вершина в точке (х0; у0), где х0 = = –1; у0 = –1. Точки пересечения с осями координат находим из уравнения х2 + 2х = 0;
| х (х + 2) = 0; х1 = 0, х2 = –2. (0; 0); (–2; 0). |  |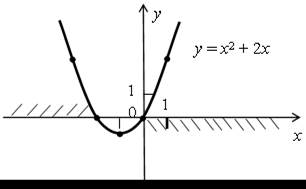
Функция принимает положительные значения, если х (–∞; –2)
(0; +∞).
6. Общее число книг 8 + 4 = 12. Исходами опыта являются все возможные сочетания из 5 книг (порядок значения не имеет).
Общее число исходов:
.Событие А – «из выбранных книг – 3 приключенческих романа и 2 сборника стихотворений».
Количество благоприятных исходов:
.Искомая вероятность:
.О т в е т: .
7. Пусть х км – расстояние между пунктами А и В, тогда (ч) – время, которое автобус должен был быть в пути. Половину пути автобус проехал за (ч), а вторую половину за
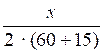
(ч). Зная, что он еще и простоял ч, но приехал в пункт В вовремя, составим уравнение:
;75х + 4500 + 60х – 150х = 0;
15х = 4500;
х = 300.
О т в е т: 300 км.
У р о к 17 (101).
АНАЛИЗ ИТОГОВОЙ КОНТРОЛЬНОЙ РАБОТЫ
Цели: рассмотреть, проанализировать типичные ошибки, допущенные большинством учащихся; выполнить работу над ошибками.
Ход урока
I. Организационный момент.
II. Выполнение работы над ошибками.
Осуществляем поиск ошибок, анализируем, повторяем теоретический материал и решаем заново упражнения, в которых допущены ошибки.
III. Формирование умений и навыков.
Учащиеся, получившие отметку «отлично» или выполнившие работу над ошибками, приступают к решению заданий, соответствующих перечню контролируемых на государственной итоговой аттестации вопросов.
Задания представлены в двух частях. Часть I направлена на проверку достижения уровня базовой подготовки учащихся по алгебре. Часть II предназначена для дифференцированной проверки повышенного уровня алгебраической подготовки учащихся.
Сильные в учебе учащиеся могут решать только вторую часть.
Упражнения:
Ч а с т ь I
1. Вычислите: 4,5 + 2 · 5–2.
1) –45,5; 2) –15,5; 3) 4,58; 4) 4,42.
2. Премию в 26 тыс. р. было решено распределить между тремя рабочими в отношении 2 : 4 : 7. Сколько составляет наибольшая премия?
1) 8 тыс. р.; 2) 14 тыс. р.; 3) 16 тыс. р.; 4) 18 тыс. р.
3. Упростите выражение:
.1) х + 8; 2) ; 3)
; 4) .
4. Разложите на множители: 81x6y4 – 0,36z2.
1) (9x3y2 – 0,6z)2;
2) (9x4y2 – 0,6z)2;
3) (9x3y2 – 0,6z) (9x3y2 + 0,6z);
4) (9x4y2 – 0,6z) (9x4y2 + 0,6z).
5. Найдите количество корней уравнения:
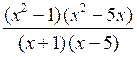= 0.О т в е т: _______.
6. Решите неравенство: 2х – х2 < 0.
1) (0; 2); 3) (–∞; 0) (2; +∞);
2) (2; +∞); 4) (–∞; 2).
7. Решите систему уравнений:
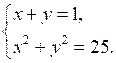
О т в е т: ______.
8. Арифметическая прогрессия задана формулой ап = 37,3 – 0,3п. Найдите номер наибольшего отрицательного члена прогрессии.
О т в е т: ______.
О т в е т ы:
| Номер задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Ответ | 3 | 2 | 1 | 3 | 2 | 3 | (–3; 4); (4; –3) | 125 |
Ч а с т ь II
1. Решить неравенство: х3 – х2 – 6х < 0.
Р е ш е н и е
х3 – х2 – 6х < 0;
х (х2 – х – 6) < 0;
х (х – 3) (х + 2) < 0.
(–∞; –2) (0; 3).
О т в е т: (–∞; –2) (0; 3).
2. Две машинистки, работая вместе, могут напечатать 22 страницы текста за 1 ч. Чтобы напечатать 120 страниц текста, первая машинистка потратит на 2 ч больше, чем вторая. За сколько часов первая машинистка сможет напечатать 300 страниц текста?
Р е ш е н и е
А н а л и з:
| | p (с./ч) | t (ч) | A (с.) | |
| I, II | p1 + p2 | 1 | 22 | |
| I | p1 | |  > на 2 ч | 120 |
| II | p2 | | 120 | |
А = р · t
Пусть х с./ч – производительность первой машинистки, тогда (22 – х) с./ч – производительность второй машинистки. На печать 120 страниц первая машинистка затратит ч, а вторая
ч. Зная, что первая машинистка затратила на 2 ч больше, составим уравнение:–
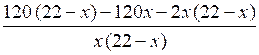= 2; = 0;при х ≠ 0, х ≠ 22 2640 – 120х – 120х – 44х + 2х2 = 0;
х2 – 142х + 1320 = 0;
D1 = (71)2 – 1320 = 3721;
х1 = 71 + 61 = 132 – не удовлетворяет условию задачи (х < 22);
х2 = 71 – 61 = 10;
= 30 (ч) – затратит первая машинистка.
О т в е т: 30 ч.
3. Найдите сумму всех положительных трехзначных чисел, не делящихся на 13.
Р е ш е н и е
Количество трехзначных чисел равно 900 (100 ≤ х ≤ 999). Найдем сумму всех этих чисел и вычтем из нее сумму чисел, делящихся на 13.
1) (ап) – арифметическая прогрессия, где а1 = 100, ап = 999, d = 1.
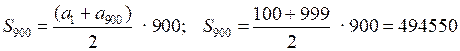.2) (bn) – арифметическая прогрессия, b1 = 104, d = 13, bn ≤ 999.
bn = 104 + 13 (п – 1) = 91 + 13п;
91 + 13п ≤ 999;
13п ≤ 908;
п ≤ 69,8, п = 69;
; .3) 494550 – 37674 = 456876.
О т в е т: 456876.
4. Упростите выражение:
.Р е ш е н и е