ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1019
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Ход урока
I. Организационный момент.
II. Устная работа.
Сколько решений имеет система уравнений, если графики уравнений, входящих в нее, изображены ниже на рисунке?
а)
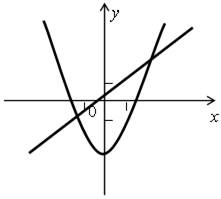б) 
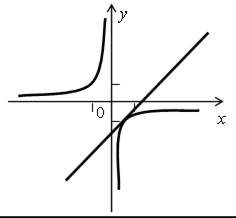
в)
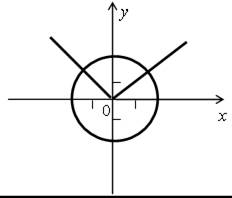
III. Проверочная работа.
В а р и а н т 1
Решите графически систему уравнений:
а)
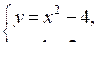б)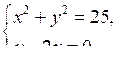 
В а р и а н т 2
Решите графически систему уравнений:
а)
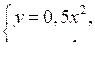б)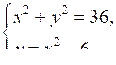 
IV. Формирование умений и навыков.
Упражнения:
1. № 420, № 422.
2. № 421.
После выполнения № 421 можно поставить перед учащимися вопрос: сколько решений может иметь система уравнений? При поиске ответа на этот вопрос предложить им использовать графические представления.
В итоге, учащиеся должны прийти к выводу, что система уравнений может иметь одно, два, три, четыре решения, а может не иметь решений. К каждой из этих ситуаций учащиеся в тетрадях должны изобразить по несколько примеров.
О д н о р е ш е н и е:
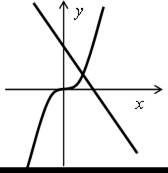
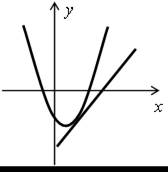
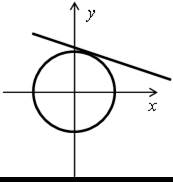
Д в а р е ш е н и я:
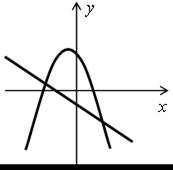
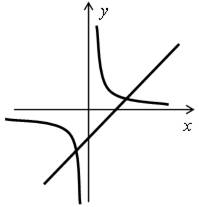
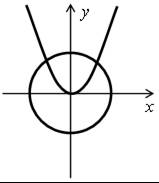
Т р и р е ш е н и я:
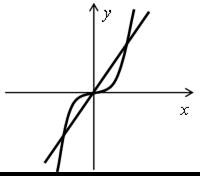
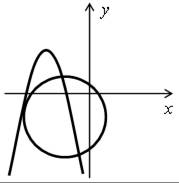
Ч е т ы р е р е ш е н и я:
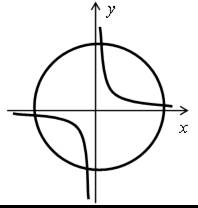
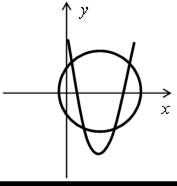
Н е т р е ш е н и й:
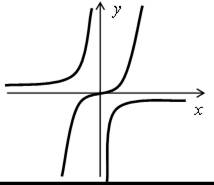
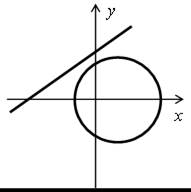
В классе с высоким уровнем подготовки можно дополнительно выполнить еще несколько номеров.
1. № 423.
Р е ш е н и е
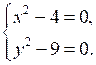
Графиком уравнения х2 – 4 = 0 будут две прямые: х = 2 и х = –2, а графиком уравнения у2 – 9 = 0 – прямые у = 3 и у = –3.
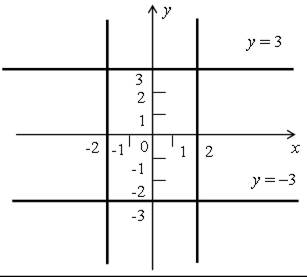
Таким образом, данная система имеет 4 решения.
О т в е т: (–2; 3), (–2; –3), (2; 3), (2; –3).
2. № 525.
Р е ш е н и е
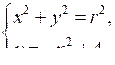
Графиком уравнения х2 + у2 = r2 является окружность с центром в начале координат и радиусом r. Графиком уравнения у = – х2 + 4 является парабола.
Для нахождения возможного количества решений этой системы нужно построить параболу и рассмотреть варианты расположения окружности х2 + у2 = r2 относительно этой параболы.
В результате получаем следующие графические иллюстрации:
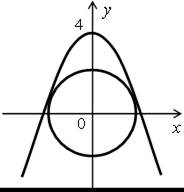
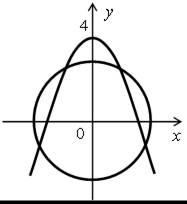
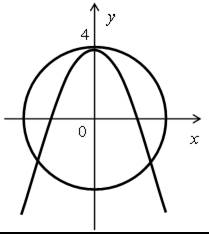
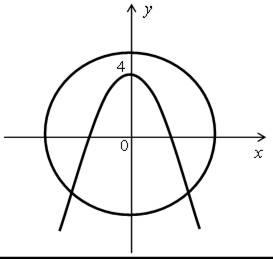
Таким образом, данная система уравнений может иметь два, три, четыре решения, а может не иметь решений.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– В чем состоит суть графического способа решения систем уравнений?
– Что такое решение системы уравнений?
– Сколько может иметь решений система уравнений?
Домашнее задание: № 419, № 524.
Д о п о л н и т е л ь н о: № 526.
У р о к 42 Дата:
СУТЬ СПОСОБА ПОДСТАНОВКИ РЕШЕНИЯ
СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ
Цели: изучить способ подстановки решения систем уравнений второй степени; формировать умение применять этот способ.
Ход урока
I. Организационный момент.
II. Устная работа.
Является ли пара чисел (–2; 3) решением системы уравнений?
а) б)
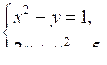
III. Объяснение нового материала.
Сначала необходимо актуализировать знания учащихся, предложив им решить способом подстановки систему линейных уравнений:
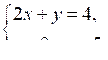
Можно разбить учащихся на два варианта и к доске вызвать двоих учеников. Один вариант решает эту систему, выражая переменную х через у, а другой – переменную у через х.
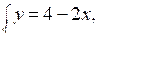 х – 12 + 6х = –5; 7х = 7; х = 1; у = 4 – 2 · 1 = 2. О т в е т: (1; 2). | 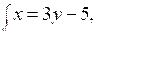 6у – 10 + у = 4; 7у = 14; у = 2; х = 3 · 2 – 5 = 1. О т в е т: (1; 2). |
После того как учащиеся вспомнили, в чем состоит способ подстановки решения систем линейных уравнений, сообщить им, что этот способ может применяться и для решения систем уравнений второй степени.
Разобрав примеры из учебника, учащиеся должны заметить, что в системе линейных уравнений можно выражать переменную из любого уравнения, а в системе уравнений второй степени это не всегда удается.
IV. Формирование умений и навыков.
Упражнения:
1. № 429 (а, в), № 431 (а, в).
2. № 433 (а, в, д).
Перед решением каждой из систем можно спрашивать учащихся о возможном количестве ее корней. Ответ на этот вопрос учащиеся могут получить, исходя из графических представлений. Затем свои предположения они проверяют аналитически.
Н а п р и м е р, система
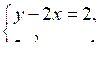(№ 433 (а)) состоит из уравнений, задающих прямую и параболу. Графики этих уравнений могут пересекаться в одной и двух точках, а могут и не пересекаться. Значит, данная система может иметь либо один, либо два корня, а может не иметь корней.После таких рассуждений решаем эту систему уравнений:
у = 2х + 2;
5х2 – (2х + 2) = 1;
5х2 – 2х – 3 = 0;
D1 = 1 + 15 = 16;
x1 = = 1 y1 = 2 ∙ 1 + 2 = 4;
x2 = = – y2 = 2 ∙ + 2 = .
Получаем, что данная система имеет два решения.
О т в е т: (1; 4), .
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Сколько решений может иметь система линейных уравнений?
– Сколько решений может иметь система уравнений второй степени?
– Опишите, какие действия нужно совершить, чтобы решить систему уравнений второй степени способом подстановки.
Домашнее задание: № 430, № 431 (б, г), № 433 (б, г, е).
У р о к 43 Дата:
РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ
СПОСОБОМ ПОДСТАНОВКИ
Цели: продолжить формирование умения решать системы уравнений второй степени способом подстановки.
Ход урока
I. Организационный момент.
II. Устная работа.
Какие из пар чисел (–2; 1), (3; 6), (1; –2) являются решением системы уравнений
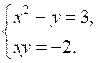
III. Формирование умений и навыков.
Упражнения:
1. № 434 (а, д), № 435 (а), № 436 (а), № 437 (а).
2. № 440.
3. № 441.
Р е ш е н и е
б)
