ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1018
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
7. Из пункта А в пункт В, расстояние между которыми 45 км, выехал велосипедист. Через 30 мин вслед за ним выехал второй велосипедист, который прибыл в п. В на 15 мин раньше первого. Какова скорость первого велосипедиста, если она на 3 км/ч меньше скорости второго?
В а р и а н т III
1. Упростите выражение:
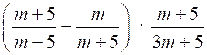.2. Решите систему уравнений:
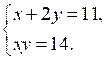
3. Решите неравенство: 5х – 3 (х – 1,5) < 4х + 1,5.
4. Найдите значение выражения
при n = .5. Постройте график функции у = х2 – 2х. Укажите, при каких значениях х функция принимает отрицательные значения.
6. В корзине находятся 10 маслят и 3 подосиновика. Из нее наугад берут 5 грибов. Какова вероятность, что среди выбранных грибов окажется 3 масленка и 2 подосиновика?
7. В фермерском хозяйстве благодаря применению новых технологий урожайность пшеницы возросла на 3 ц с га. В результате было собрано не 190 ц пшеницы, как в предшествующем году, а 198 ц, хотя под пшеницу отвели на 1 га меньше. Какая площадь была отведена в хозяйстве под пшеницу в эти годы?
В а р и а н т IV
1. Упростите выражение:
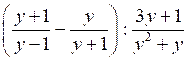.2. Решите систему уравнений:
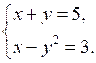
3. Решите неравенство: х – 2,5 (2х – 1) > х – 1,5.
4. Найдите значение выражения
при с = .5. Постройте график функции у = х2 + 2х. Укажите, при каких значениях х функция принимает положительные значения.
6. На полке находятся 8 приключенческих романов и 4 сборника стихотворений. Из них наугад выбирают 5 книг. Какова вероятность, что среди выбранных книг окажется 3 приключенческих романа и 2 сборника стихотворений?
7. Расстояние от пункта А до пункта В автобус должен был проехать со скоростью 60 км/ч. Однако на середине пути он задержался на 30 мин и, чтобы прибыть в пункт
В без опоздания, увеличил скорость на 15 км/ч. Каково расстояние между пунктами А и В?
Р е к о м е н д а ц и и п о о ц е н и в а н и ю.
Для получения отметки «3» достаточно выполнить верно любые три из первых четырех заданий; для получения отметки «5» – любые шесть заданий.
РЕШЕНИЕ ВАРИАНТОВ КОНТРОЛЬНОЙ РАБОТЫ
В а р и а н т I
1.
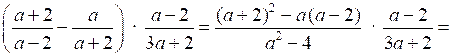
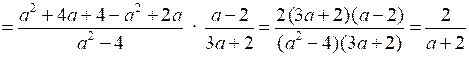.О т в е т: .
2.
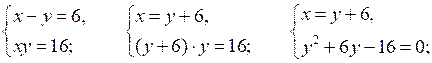
О т в е т: (–2; –8), (8; 2).
3. 5х – 1,5 (2х + 3) < 4х + 1,5;
5х – 3х – 4,5 < 4х + 1,5;
5х – 3х – 4х < 1,5 + 4,5;
–2х < 6;
х > –3.
О т в е т: х > –3.
4.
;
;
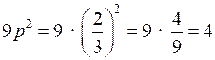.О т в е т: 81.
5. у = х2 – 4. Графиком является парабола, полученная из графика функции у = х2 сдвигом вниз на 4 единицы. Значит, вершина параболы находится в точке (0; –4).
Точки пересечения параболы с осью х находим из уравнения:
| х2 – 4 = 0; х = ± 2. (–2; 0); (2; 0). |  |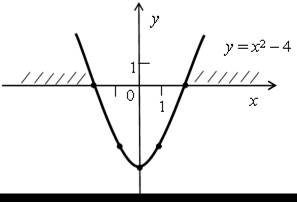
Функция принимает положительные значения, если х (–∞; –2)
(2; +∞).
6. Общее число певцов 7 + 3 = 10. Исходами опыта являются все возможные сочетания из 4 человек (порядок значения не имеет).
Общее число исходов: n =
= 210.
Событие А – «из выбранных певцов два мальчика и две девочки». Количество благоприятных исходов:
тА =
= 63.Искомая вероятность:
.О т в е т: 0,3.
7. Пусть х га – площадь I участка, тогда (х + 3) га – площадь второго участка. Урожайность на I участке составляет ц/га, а на втором ц/га. Зная, что урожайность на I участке на 2 ц/га больше, чем на втором, составим уравнение:
– = 2;
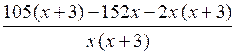= 0;при х ≠ 0, х ≠ –3 105х + 315 – 152х – 2х2 – 6х = 0;
2х2 + 53х – 315 = 0;
D = (53)2 – 4 · 2 · (–315) = 5329;
x1 =
= 5;x2 =
= –31,5 – не удовлетворяет условию (х > 0).5 (га) – площадь I участка.
5 + 3 = 8 (га) – площадь II участка.
О т в е т: 5 га; 8 га.
В а р и а н т II
1.
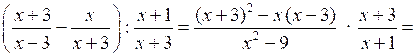
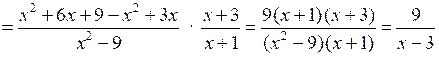.О т в е т: .
2.
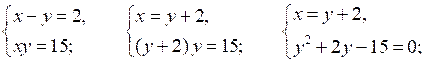
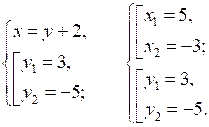
О т в е т: (5; 3); (–3; –5).
3. 2х – 4,5 > 6х – 0,5 (4х – 3);
2х – 4,5 > 6х – 2х + 1,5;
–2х > 6;
х < –3.
О т в е т: х < –3.
4.
;
;
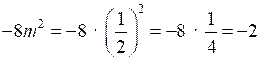.О т в е т: 0,04.
5. у = –х2 + 1. Графиком является парабола, полученная из графика
у = х2 отражением относительно оси
х и сдвигом вверх на 1 единицу. Значит, вершина параболы находится в очке (0; 1).
Точки пересечения параболы с осью х находим из уравнения:
| –х2 + 1 = 0; х2 = 1; х = ±1. (–1; 0); (1; 0). |  |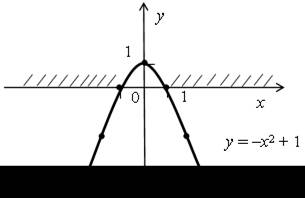
Функция принимает отрицательные значения, если х (–∞; –1)
(1; +∞).
6. Общее число конфет 6 + 4 = 10. Исходами опыта являются все возможные сочетания из 4 конфет (порядок значения не имеет).
Общее число исходов:
.Событие А – «из выбранных конфет две со сливочной начинкой и две с шоколадной». Количество благоприятных исходов:
Искомая вероятность:
.О т в е т: .
7. Пусть х км/ч – скорость 1-го велосипедиста, тогда (х + 3) км/ч – скорость второго велосипедиста. На весь путь 1-й и 2-й велосипедисты затратили соответственно ч и ч. Зная, что 1-й велосипедист был в пути на
ч дольше второго, составим уравнение:
;
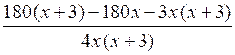= 0;при х ≠ 0, х ≠ –3 540 –3х2 – 9х = 0;
х2 + 3х – 180 = 0.
D = 9 – 4 · 1 · (–180) = 729;
x1 = = 12;
x2 = = –15 – не удовлетворяет условию задачи (х > 0).
О т в е т: 12 км/ч.
В а р и а н т III
1.
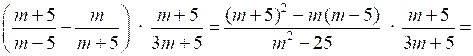
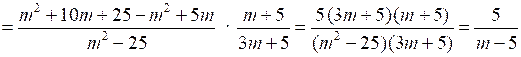.О т в е т: .
2.
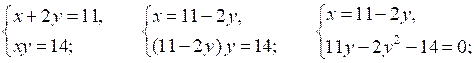
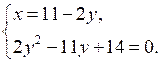
2у2 – 11у + 14 = 0;
D = 121 – 4 · 2 · 14 = 9;
y1 =
= 3,5; х1 = 11 – 2 · 3,5 = 4;y2 = = 2; х2 = 11 – 2 · 2 = 7.
О т в е т: (4; 3,5), (7; 2).
3. 5х – 3 (х – 1,5) < 4х + 1,5;
5х – 3х + 4,5 < 4х + 1,5;
5х – 3х – 4х < 1,5 – 4,5
–2х < –3;
х > 1,5.
О т в е т: х > 1,5.
4.
;
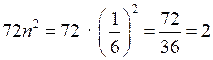
.О т в е т: 36.
5. у = х2 – 2х. Графиком является парабола, вершина в точке (х0, у0), где х0 = = 1, у0 = –1. Точки пересечения с осями координат находим из уравнения х2 – 2х = 0; х (х – 2) = 0;
| х1 = 0, х2 = 2. (0; 0), (2; 0). |  |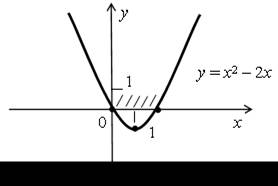
Функция принимает отрицательные значения, если х (0; 2).
6. Общее число грибов 10 + 3 = 13. Исходами опыта являются все возможные сочетания из 5 грибов (порядок значения не имеет).
Общее число исходов:
.Событие А – «из выбранных грибов 3 масленка и 2 подосиновика». Количество благоприятных исходов:
.Искомая вероятность:
.О т в е т: .
7. Пусть х га было отведено под пшеницу в прошлом году, тогда (х – 1) га отвели под нее в этом году. Урожайность пшеницы в этом и прошлом году составляла соответственно ц/га и ц/га. Зная, что урожайность пшеницы повысилась на 3 ц/га, составим уравнение:
– = 3;
