ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1021
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
О т в е т: у > 0, если х > 0; у < 0, если х < 0.
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какая зависимость называется функцией?
– Назовите основные свойства линейной функции, квадратичной, обратной пропорциональности.
– Приведите алгебраическую и геометрическую интерпретацию указанных свойств.
Домашнее задание: № 1021 (г), № 1025, № 1027, № 1028 (а, д).
У р о к 14 (98).
СООТНОШЕНИЕ АЛГЕБРАИЧЕСКОЙ
И ГЕОМЕТРИЧЕСКОЙ МОДЕЛЕЙ ФУНКЦИИ
Цели: актуализировать умения решать задачи на связь функций и их графиков (определять путем вычисления взаимное расположение графиков функций, вычислять наибольшее (наименьшее) значение функции и прочее).
Ход урока
I. Организационный момент.
II. Устная работа.
Найти область определения функции:
а) у = ; б) у = ; в) ; г) ;
д) у =
; е) 
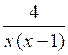; ж) у = ; з) у = .III. Формирование умений и навыков.
Суть заданий состоит в том, чтобы, не прибегая к построению графиков, аналитическим путем выявлять основные свойства функции: промежутки знакопостоянства, точки пересечения с осями координат, взаимное расположение графиков функций. График изображаем либо схематически, либо после преобразования аналитической модели функции.
Упражнения:
№ 1029 (а; г).
Р е ш е н и е
а) у = 2х2 + 10х – 7 – квадратичная функция, график – парабола, ветви направлены вверх. Пусть х0 – абсцисса вершины параболы, тогда функция убывает на (–∞; х0] и возрастает на [х0; +∞).
Вычислим: х0 = ; х0 = = –2,5.
Значит, на (–∞; –2,5] функция убывает; на [2,5; +∞) – функция возрастает.
г) у = 3х – 5х2 – квадратичная функция, график – парабола, ветви направлены вниз. Пусть х0 – абсцисса вершины параболы, тогда функция возрастает на (–∞;
х0] и убывает на [х0; +∞).
Вычислим: х0 = ; х0 =
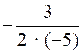= 0,3.Значит, на (–∞; 0,3] функция возрастает; на [0,3; +∞) – функция убывает.
О т в е т: а) на (–∞; –2,5] убывает; на [2,5; +∞) – возрастает; г) на (–∞; 0,3] – возрастает; на [0,3; +∞) – убывает.
№ 1032 (б, г).
Р е ш е н и е
б) у = –3х – 10 и у = х2 – 13х + 6 пересекаются в точках, абсциссы которых являются решением уравнения:
–3х – 10 = х2 – 13х + 6;
х2 – 10х + 16 = 0;
по теореме Виета, х1 = 2; х2 = 8.
Для нахождения ординат точек подставим значение х в любую из формул (удобнее в формулу линейной функции):
у1 = у (х1) = –3 · 2 – 10; у1 = –16;
у2 = у (х2) = –3 · 8 – 10; у2 = –34.
(2; –16), (8; –34).
г) у = 4х2 + 3х + 6 и у = 3х2 – 3х – 3;
4х2 + 3х + 6 = 3х2 – 3х – 3;
х2 + 6х + 9 = 0;
(х + 3)2 = 0;
х + 3 = 0;
х = –3.
у (–3) = 4 · (–3)2 + 3 (–3) + 6 = 36 – 9 + 6 = 33;
(–3; 33).
О т в е т: б) (2; –16), (8; –34); г) (–3; 33).
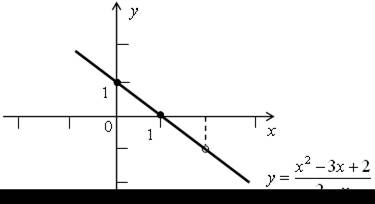
№ 1034 (в).
Р е ш е н и е
у =
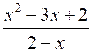; D (у) = (–∞; 2) (2; +∞).х2 – 3х + 2 = (х – 2) (х – 1).
При х ≠ 2
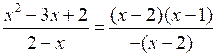= 1 – х.у = 1 – х – линейная функция, график – прямая.
| х | 0 | 3 |
| у | 1 | –2 |
№ 1035 (в).
Р е ш е н и е
у =
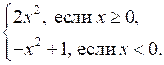
у = 2х2 – графиком является парабола, полученная из графика у = х2 «растяжением» вдоль оси у в 2 раза.
у = –х2 + 1, графиком является парабола, полученная из графика у = х2 «отражением» относительно оси
х и смещением вверх на 1 единицу.
IV. Проверочная работа (тестирование).
В а р и а н т 1
1. Функция задана графиком. Укажите область определения этой функции.
| 1) [–2; 4); 2) [–2; 4]; 3) [–2; –1) (–1; 4]; 4) [–2; –1) (–1; 2]. |  |
2. Функция задана графиком. Укажите множество значений этой функции.
| 1) (–4; 1]; 2) [–2; 2]; 3) (–4; 2]; 4) (–3; 2]. |  |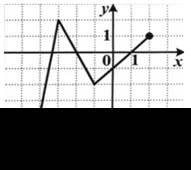
3. Укажите промежутки убывания функции у = f (х), заданной графиком на интервале (–5; 7).
| 1) (–5; 1]; [3; 5]; 2) [–1; 3]; [5; 7); 3) (–5; –1]; [3; 6]; 4) [–2; 3]; [5; 7). |  |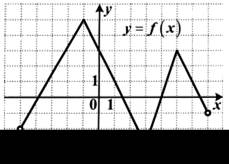
4. Укажите наибольшее значение функции у = g (х), заданной на отрезке [–4; 4].
| 1) –4; 2) 2; 3) 3; 4) 4. |  |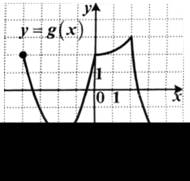
5. Какая из парабол проходит через начало координат?
1) у = х2 – 2х;
2) у = х2 – 2;
3) у = –х2 – 2;
4) у = (х – 2)2.
В а р и а н т 2
1. Найдите область определения функции, график которой изображен на рисунке.
| 1) (–3; 5); 2) (–3; 4]; 3) [–3; 3) (3; 4]; 4) (–3; 5]. |  |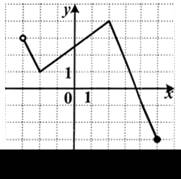
2. Функция задана графиком. Найдите область значений этой функции.
| 1) [–4; 4]; 2) [–4; 4); 3) [–3; 3); 4) [–4; 3). |  |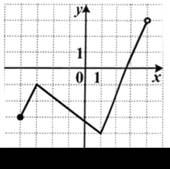
3. Найдите промежутки возрастания функции у = g (х), заданной графиком на полуинтервале [–4; 4).
| 1) [–4; –3]; [–2; 1]; 2) [–3; –2]; [0; 4]; 3) [–3; –2]; [1; 4); 4) [–4; –3]; [–2; 0]. |  |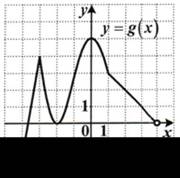
4. Укажите наименьшее значение функции у = f (х), заданной на отрезке [–4; 4].
| 1) –3; 2) –4; 3) –5; 4) 4. |  |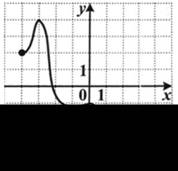
5. Какая из парабол проходит через начало координат?
1) у = х2 + 2;
2) у = х2 + 2х;
3) у = –х2 + 2;
4) у = (х + 2)2.
О т в е т ы:
| В а р и а н т 1 1. 1) 2. 3) 3. 2) 4. 3) 5. 1) | В а р и а н т 2 1. 4) 2. 4) 3. 4) 4. 2) 5. 2) |
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Задайте аналитически следующие условия:
а) график функции f (х) расположен выше оси абсцисс на всей ОДЗ.
б) Графики функций f (х) и g (х) пересекаются в точке А (х0; у0).
в) Вершина параболы расположена в точке (1; –2).
– Как расположен график функции f (х), если:
а) f (х) ≥ 0, для х (0; 18];
б) f (х0) = g (х0), где х0 = 2;
в) f (х) = 4.
Домашнее задание: № 1032 (а, в), № 1033, № 1034 (а), № 1035 (б). Подготовка к итоговой контрольной работе.
У р о к и 15–16 (99–100).
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА
В а р и а н т I
1. Упростите выражение:
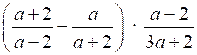.2. Решите систему уравнений:
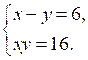
3. Решите неравенство 5х – 1,5 (2х + 3) < 4х + 1,5.
4. Найдите значение выражения
при p = .5. Постройте график функции у = х2 – 4. Укажите, при каких значениях х функция принимает положительные значения.
6. В школьном хоре поют 7 мальчиков и 3 девочки. По жребию отбирают 4 человека для участия в гала-концерте. Какова вероятность, что среди отобранных певцов окажется 2 мальчика и 2 девочки?
7. В фермерском хозяйстве под гречиху было отведено два участка. С первого собрали 105 ц гречихи, а со второго, площадь которого на 3 га больше, собрали 152 ц. Найдите площадь каждого участка, если известно, что урожайность гречихи на первом участке была на 2 ц с 1 га больше, чем на втором.
В а р и а н т II
1. Упростите выражение:
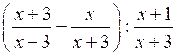.2. Решите систему уравнений:
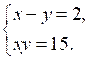
3. Решите неравенство: 2х – 4,5 > 6х – 0,5 (4х – 3).
4. Найдите значение выражения
при m = .5. Постройте график функции у = –х2 + 1. Укажите, при каких значениях х функция принимает отрицательные значения.
6. В коробке находятся 6 конфет со сливочной начинкой и 4 с шоколадной. Из нее наугад берут 4 конфеты. Какова вероятность, что среди выбранных конфет окажется 2 со сливочной начинкой и 2 с шоколадной?