Файл: Учебнометодическое пособие для направлений подготовки 44. 03. 01 Педагогическое образование и 44. 03. 05 Педагогическое образование (с двумя профилями подготовки).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 307
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
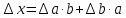 ,
,относительная погрешность
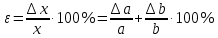
-
Если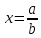 , то
, то
абсолютная погрешность
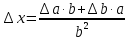 ,
,относительная погрешность

-
Если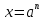 , то
, то
абсолютная погрешность
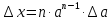 ,
,относительная погрешность
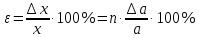
-
Если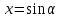 , то
, то
абсолютная погрешность
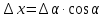 ,
,относительная погрешность
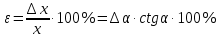
-
Если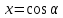 , то
, то
абсолютная погрешность
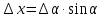 ,
,относительная погрешность
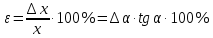
-
Если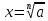 , то
, то
абсолютная погрешность
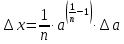 ,
,относительная погрешность
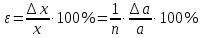
-
Если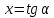 , то
, то
абсолютная погрешность
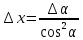 ,
,относительная погрешность
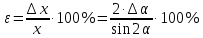
-
Если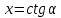 , то
, то
абсолютная погрешность
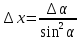 ,
,относительная погрешность
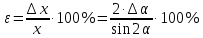
Приведем некоторые табличные данные, которые вам помогут при выполнении лабораторных работ.
плотность вещества,
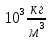
| Газы (при нормальных условиях) | |||
| Воздух | 0,001293 | Кислород | 0,001429 |
| Углекислый газ | 0,001977 | Водород | 0,00008988 |
| Жидкости | |||
| Бензол | 0,88 | Спирт | 0,79 |
| Керосин | 0,80 | Ртуть | 13,6 |
| Скипидар | 0,85 | Эфир (200С) | 0,714 |
| Касторовое масло | 0,97 | Глицерин | 1,21 |
| Твердые вещества | |||
| Висмут | 9,7 | Медь | 8,9 |
| Вольфрам | 19,0 | Натрий хлористый | 2,17 |
| Гуммигут | 1,2 | Никель | 8,8 |
| Железо | 7,8 | Свинец | 11,3 |
| Лед | 0,917 | Цинк | 7,0 |
| Латунь | 8,5 | Эбонит | 1,15 |
| Сосна | 0,4 | Акция (белая) | 0,63 |
| Береза | 0,56 | Дуб | 0,9 |
| Груша | 0,72 | Алюминий | 2,7 |
Фундаментальные постоянные
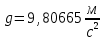 - ускорение свободного падения
- ускорение свободного падения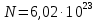 – постоянная Авогадро (число молекул в 1 моле)
– постоянная Авогадро (число молекул в 1 моле)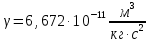 - гравитационная постоянная
- гравитационная постояннаяАстрономические величины
6370 км – средний радиус Земли
5,96 1024 кг – масса Земли
Некоторые часто встречающиеся числа
| Число | n | lg n |
| π | 33,141593 | 0,49715 |
| 4 π | 12,56637 | 1,09921 |
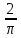 | 0,63662 | 1,80388 |
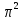 | 9,86960 | 0,99430 |
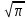 | 1,77245 | 0,24857 |
| e | 2,718282 | 0,43429 |
| ln 10 | 2,3026 | 0,33222 |
| ln 2 | 0,6931 | |
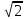 | 1,41421 | 0,15052 |
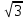 | 1,73205 | 0,23856 |
| 10 | 0,017453 радиана | |
| 1’ | 0,000291 радиана | |
| 1” | 0,0000048 радиана | |
Соотношения между механическими единицами СИ и системами СГС
| Название величины и её обозначение | Единицы СИ | Единицы СГС | Отношение 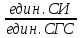 | ||||
| Название | Обозначение | Название | Обозначение | | |||
| Длина l | Метр | м | Сантиметр | см | 102 | ||
| Площадь S | Квадратный метр | м2 | Квадратный сантиметр | см2 | 104 | ||
| Объем V | Кубический метр | м3 | Кубический сантиметр | см3 | 106 | ||
| Время t,τ | Секунда | с | Секунда | с | 1 | ||
| Частота колебаний 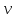 | Герц | Гц | Герц | Гц | 1 | ||
| Частота вращения 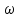 | | с-1 | | с-1 | 1 | ||
| Скорость 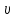 | | 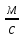 | кин | 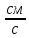 | 102 | ||
| Угловая скорость 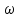 | | 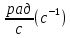 | | 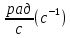 | 1 | ||
| Ускорение a | | 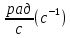 | гал | 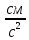 | 102 | ||
| Угловое ускорение 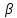 | | 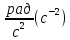 | | 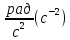 | 1 | ||
| Масса m | Килограмм | кг | Грамм | г | 103 | ||
| Сила F | Ньютон | Н | Дина | дин | 105 | ||
| Давление P | | Па | | 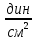 | 10 | ||
| Плотность 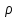 | |  | | 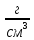 | 10-3 | ||
| Момент силы M | | 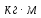 | | 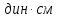 | 107 | ||
| Момент инерции I | | 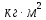 | | 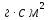 | 107 | ||
| Импульс p | | 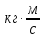 | | 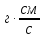 | 105 | ||
| Момент импульса L | | 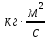 | | 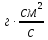 | 107 | ||
ЛАБОРАТОРНАЯ РАБОТА № 1
Определение плотности твердых тел,
имеющих правильную геометрическую форму
Цель работы: ознакомление с измерительными приборами (штангенциркуль, микрометр, технические весы), и методом, служащим для измерения плотности твердых тел, имеющих правильную геометрическую форму.
Принадлежности: штангенциркуль, микрометр, технические весы, разновески, два тела правильной геометрической формы (параллелепипед и цилиндр сложной формы).
Введение
Масштаб и нониус. Для измерения линейных размеров тел применяются масштаб и нониус.
Масштабом называется линейка, разделенная, чаще всего, на миллиметры и сантиметры.
Нониусом называется дополнительное приспособление к масштабу, позволяющее повысить точность измерения.
Н
 ониус (рис. 1) представляет собой линейку, скользящую вдоль масштаба. На этой линейке нанесено
ониус (рис. 1) представляет собой линейку, скользящую вдоль масштаба. На этой линейке нанесено 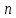 делений, которые «разбивают» наименьшее деление масштаба на
делений, которые «разбивают» наименьшее деление масштаба на 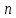 частей, то есть одно деление нониуса составляет
частей, то есть одно деление нониуса составляет 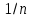 часть деления масштаба.
часть деления масштаба.Это обстоятельство, таким образом, дает возможность измерять с помощью нониуса сотые (иногда десятые) доли деления масштаба. В самом деле, если совместить нулевое деление нониуса с каким-либо делением масштаба, то все остальные деления нониуса не будут совпадать с делениями масштаба (кроме последнего деления нониуса).
Если же сдвинуть нониус вправо так, чтобы первое деление нониуса совпало с каким-нибудь делением масштаба, то между нулевым делением нониуса и ближайшим к нему слева делением масштаба образуется промежуток в
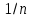 часть деления масштаба.
часть деления масштаба.Если же с делением масштаба будет совпадать не первое, а k-тое деление нониуса, то расстояние между нулевым делением нониуса и ближайшим к нему слева делением масштаба будет в k раз больше, то есть
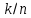 .
.
Итак, отсчет с помощью масштаба и нониуса состоит в следующем:
а) отсчитывается целое число L делений масштаба до нулевого деления нониуса;
б) определяется, какое деление (первое по счету) нониуса совпадает с делением масштаба;
в) производится расчет размера по формуле:
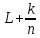 .
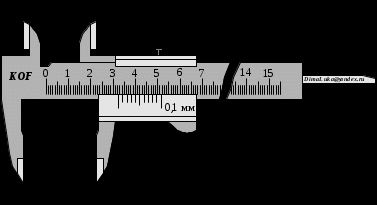
.Смотрите пример (рис. 2). Исходя из рисунка:
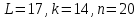 . Тогда получим:
. Тогда получим: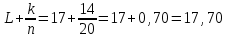 ;
;если масштаб в миллиметрах, то получим 17,70 мм.

Штангенциркуль. Штангенциркуль предназначен для измерения, с достаточно высокой степенью точности, линейных размеров тел имеющих небольшие длины. Основной его частью (рис. 3) является линейка 1 – называемая масштабом (смотрите выше). Линейка снабжена двумя ножками: неподвижной ножкой 2 и подвижной ножкой 3, скрепленной с рамкой 4, на которой нанесены деления шкалы называемой нониусом (смотрите выше). Рамка 4 может закрепляться на линейке 1 с помощью винта 5. Если сдвинуть ножки штангенциркуля вплотную, то нулевые деления нониуса и масштаба должны совпасть. Зажимая между ножками штангенциркуля измеряемый предмет, можно определить его длину по масштабу и нониусу (смотрите выше). Модель штангенциркуля изображенного на рисунке предназначена для измерения внешних и внутренних размеров, а также размеров выемок, пазов и так далее.
Микрометр. Микрометр предназначен для измерения, с очень высокой степенью точности, линейных размеров тел имеющих небольшие длины.
Микрометр состоит (рис. 4) из стальной скобы 1, к которой присоединяется трубка 2, имеющая внутреннюю винтовую нарезку. (При измерении микрометр держат так, чтобы скоба 1 была слева, а трубка 2 располагалась справа от нее.) В трубку 2 входит винт, скрепленный с гильзой 3 и выходящий наружу в виде стержня 4. На трубке 2 нанесен миллиметровый масштаб (смотрите выше), позволяющий отсчитать, на сколько целых делений отодвинулась гильза 3 от нулевого деления масштаба. Если шаг винта равен d мм, то при одном полном обороте винт и связанная с ним гильза