Файл: Учебнометодическое пособие для направлений подготовки 44. 03. 01 Педагогическое образование и 44. 03. 05 Педагогическое образование (с двумя профилями подготовки).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 312
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ЛАБОРАТОРНАЯ РАБОТА № 6
Определение модуля упругости из растяжения проволоки
П
 ринадлежности: прибор Лермонтова, набор грузов (5 грузов) с платформами (2 платформы), технические весы, разновески, индикатор стрелочного типа, сантиметровая линейка, микрометр.
ринадлежности: прибор Лермонтова, набор грузов (5 грузов) с платформами (2 платформы), технические весы, разновески, индикатор стрелочного типа, сантиметровая линейка, микрометр.Введение
Определение модуля Юнга из растяжения проволоки основано на применении закона Гука. Под весом груза P, проволока длиной L и площадью поперечного сечения S растягивается на величину
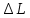 . Согласно закону Гука, имеем:
. Согласно закону Гука, имеем: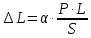 , (1)
, (1)где – коэффициент упругости при растяжении (сжатии) или коэффициент продольного удлинения (сжатия).
Модуль упругости при растяжении (сжатии) равен:
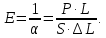 (2)
(2)Учитывая, что проволока в сечении имеет круг, окончательно получим:
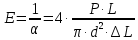 . (3)
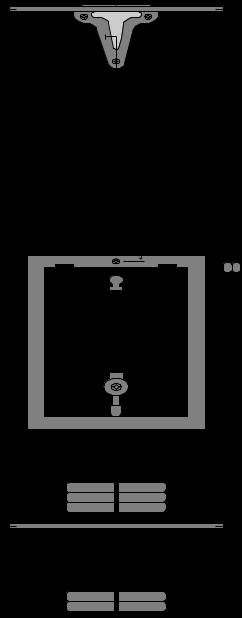
. (3)Описание прибора и методики измерения. Прибор Лермонтова (смотрите рисунок) смонтирован на вертикально установленной раме 1 (на рисунке отсутствует). Исследуемая проволока 2 диаметром d и длиной L жестко закреплена в кронштейне 3 и натянута при помощи груза 4 (металлическая прямоугольная рамка), основание которого снабжено крючком 5 для подвеса нагрузки P. Кронштейн 6 имеет арретир 7, пользуясь которым можно освобождать проволоку от нагрузки. Грузы P, необходимые для нагрузки проволоки 2 берутся с особого подвеса 8 (также снабженного крючком 5) укрепленного на верхнем кронштейне 3. (При снятии нагрузки, грузы P также укладываются на подвес 8. Этим достигается постоянство нагрузки на верхний кронштейн 3).
Нагрузку проволоки и снятие нагрузки нужно всегда производить при опущенном арретире 7.
При нагрузке, осуществляемой грузами P, проволока удлиняется на величину
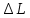 . Это удлинение фиксируется индикатором 9 (цена деления 0,01 мм).
. Это удлинение фиксируется индикатором 9 (цена деления 0,01 мм).Длина проволоки L измеряется сантиметровой линейкой (как показано на рисунке) при опущенном арретире, а ее диаметр d – микрометром.
Последовательно нагружая проволоку
2 грузами P, производят подсчет делений по шкале индикатора 9, записывая его показания. Таким образом, проделывают опыт для всех грузов снимая их с подвеса 8 (так называемый прямой переход), а затем так же последовательно идут в обратном порядке (так называемый обратный переход), снимая грузы и укладывая их на подвес 8 и также записывая показания индикатора.
Порядок выполнения задания
-
Устанавливают индикатор 9 при поднятом арретире 7 (как показано на рисунке). -
Измеряют длину нити L (измерение провести 3 раза и вычислить среднее значение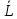 ).
). -
Измеряют диаметр нити d (измерение провести 3 раза – по середине проволоки и ближе к точкам ее закрепления; вычислить среднее значение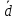 ).
). -
Измеряют массу каждого из пяти грузов в отдельности и находят их вес как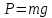 (перед началом взвешивания грузы следует пронумеровать; платформу на которую укладываются грузы взвешивать необязательно, а удлинение исследуемой проволоки, которому она способствует, можно учесть вращением подвижной шкалы индикатора 9).
(перед началом взвешивания грузы следует пронумеровать; платформу на которую укладываются грузы взвешивать необязательно, а удлинение исследуемой проволоки, которому она способствует, можно учесть вращением подвижной шкалы индикатора 9). -
Укладывают грузы (согласно нумерации) на платформу и подвешивают платформу на крючок подвеса 8. Вторую (пустую) платформу подвешивают на крючок металлической рамки 4. -
Опускают арретир 7. -
Последовательно нагружая (или снимая нагрузку) проволоку грузами, производят отсчет делений по шкале индикатора (внимание: грузы следует перекладывать очень аккуратно).
Примечание. Опыт повторить по три раза (то есть сделать три прямых и три обратных перехода). Результаты измерений занести в таблицу (дорисовать таблицу). Рассчитать значение модуля Юнга по формуле (3). Сделать подробный вывод по проделанной работе.
Таблица для первого перехода
| № | 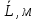 | 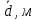 | 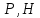 | 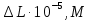 | 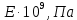 | 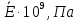 | 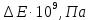 | 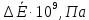 |  |  |
| Прямой переход | | | 1 | | | | | | | |
| 2 | | | | |||||||
| 3 | | | | |||||||
| 4 | | | | |||||||
| 5 | | | | |||||||
| Обратный переход | 4 | | | | ||||||
| 3 | | | | |||||||
| 2 | | | | |||||||
| 1 | | | | |||||||
| 0 | | | |
Таблица для второго перехода
| № |  |  |  |  |  |  |  |  |  |  |
| Прямой переход | | | 1 | | | | | | | |
| 2 | | | | |||||||
| 3 | | | | |||||||
| 4 | | | | |||||||
| 5 | | | | |||||||
| Обратный переход | 4 | | | | ||||||
| 3 | | | | |||||||
| 2 | | | | |||||||
| 1 | | | | |||||||
| 0 | | | |
Таблица для третьего перехода
| № |  |  |  |  |  |  |  |  |  |  |
| Прямой переход | | | 1 | | | | | | | |
| 2 | | | | |||||||
| 3 | | | | |||||||
| 4 | | | | |||||||
| 5 | | | | |||||||
| Обратный переход | 4 | | | | ||||||
| 3 | | | | |||||||
| 2 | | | | |||||||
| 1 | | | | |||||||
| 0 | | | |
Вопросы для допуска
-
Виды деформаций. -
Закон Гука (прямой и обратный). -
Модуль Юнга и его физический смысл. -
Модуль сдвига и его физический смысл. -
Примерный график зависимости упругой деформации. -
Гистерезис. Петля гистерезиса. -
Методика выполнения лабораторной работы.
Вопросы для защиты
-
Вывод закона Гука для любого вида деформации (на выбор). -
Покажите, что деформации изгиба и деформации кручения сводятся к совокупности деформаций основного вида. -
Покажите, что коэффициент объемного сжатия в 3 раза больше коэффициента линейного сжатия. Указание: тело взять в форме куба.
ЛАБОРАТОРНАЯ РАБОТА №7.
Определение массы однородного шара динамическим методом.
Цель работы: изучение свойств момента инерции; опытное определение массы однородного шара относительно оси вращения проходящей через его диаметр.
Приборы и принадлежности: однородный шар, капроновая нить, грузы (2 груза разной массы), платформа, технические весы, сантиметровая линейка, секундомер, штангенциркуль.
Введение
Если к телу, которое может вращаться около неподвижной оси, приложен вращающий момент относительно данной оси, то под его действием тело получает упругое угловое ускорение, то есть начинает вращаться. При этом вращающий момент M и угловое ускорение
 , связаны соотношением:
, связаны соотношением: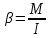 , (1)
, (1)где I - момент инерции тела относительно оси вращения, характеризует инертность тела во вращательном движении.
Момент инерции тела относительно данной оси вращения рассчитывается по формуле:
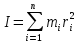 ,
,где mi- масса i-той материальной точки тела, ri- расстояние i-той материальной точки до оси вращения.
Е
 сли к телу приложен вращающий момент M, величина которого в процессе вращения остается постоянной, то вращение тела будет равноускоренным. Наблюдая равноускоренное вращения тела, под действием постоянного момента, и измеряя соответствующим образом угловое ускорение
сли к телу приложен вращающий момент M, величина которого в процессе вращения остается постоянной, то вращение тела будет равноускоренным. Наблюдая равноускоренное вращения тела, под действием постоянного момента, и измеряя соответствующим образом угловое ускорение
 , можно определить момент инерции тела относительно оси вращения:
, можно определить момент инерции тела относительно оси вращения: (2)
(2)Описание установки и метода измерения.
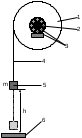
Однородный шар 1 (смотрите рисунок) жестко укреплён на валу 2. Вал может вращаться в подшипниках 3 с малым трением около горизонтальной оси. Ось вращения проходит через центр тяжести шара, через один из его диаметров. На шаре имеется маленькое отверстие для продевания капроновой нити 4, которая наматывается в несколько оборотов на шар перпендикулярно оси вращения. На свободный конец нити подвешивается груз 5 (m), приводящий всю систему в равноускоренное движение. Также крепится сантиметровая линейка 6.
Под действием груза 5 (mгруза) на маховик будет действовать вращающий момент M, равный произведению силы натяжения нити F на плечо
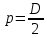 то есть:
то есть: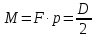 (3)
(3)где D- диаметр шара.
Если груз действует на нить с силой P, то нить действует с силой F и в соответствии с третьим законом Ньютона эти силы равны по величине и противоположны по направлению, то есть:
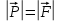 (4)
(4)Для определения силы F рассмотрим движение груза вниз. На груз действуют две силы: со стороны Земли -
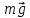 (вес груза
(вес груза 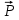 ), и со стороны нити
), и со стороны нити 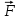 . Под действием этих сил груз будет двигаться равноускоренно с ускорением
. Под действием этих сил груз будет двигаться равноускоренно с ускорением 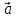 . Согласно второму закону Ньютона имеем:
. Согласно второму закону Ньютона имеем: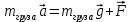 (5)
(5)где m- масса груза. Отсюда, в проекции на вертикальную координатную ось, получим:
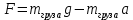 (6)
(6)где g- ускорение силы тяжести.
Вращающий момент M с учётом (4) и (6) определяется выражением
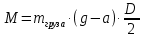 . (7)
. (7)Тогда момент инерции однородного шара на основании (2), равен: