Файл: Учебнометодическое пособие для направлений подготовки 44. 03. 01 Педагогическое образование и 44. 03. 05 Педагогическое образование (с двумя профилями подготовки).docx

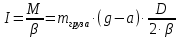(8)

где - угловое ускорение однородного шара и шкива. Угловое ускорение шкива и тангенциальное ускорение 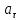точек, лежащих на его ободе, связаны следующим образом:

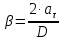(9)

Понятно, что тангенциальное ускорение 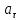, с которым вращаются точки лежащие на ободе шкива (нить, накручена на шкив), и линейное ускорение a, с которым опускается груз, равны ( )

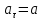Величину линейного ускорения a можно выразить из закона пути для равноускоренного движения:

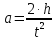(10)

где h- высота, с которой опускается груз.

С учётом (10) и (9) окончательно получим расчётную формулу для момента инерции однородного шара:

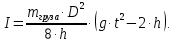(11)

Момент инерции однородного шара относительно любой оси проходящей через его диаметр равен

.

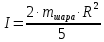Подставив значение радиуса 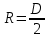, выразим значение массы шара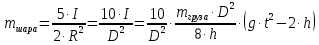



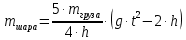(12)

Порядок выполнения работы

1. На технических весах определяются массы m₁, m₂, m₃ грузов с точностью 0,005 г.

2. Измеряют штангенциркулем диаметр шара D с точностью 0,05 мм.

3. Измеряют масштабной линейкой с точностью до 1,0 мм высоты h₁ и h₂ с которых опускается груз (измерения высот проводят от нижнего края груза до пола).

Внимание: расстояние между высотами не должно быть менее 20 см и более 40 см.

4. Определяют с точностью до 0,1 с время опускания груза m_груза с высоты h (отпуская шар, одновременно включают секундомер, а в момент удара груза о пол секундомер выключают).

Внимание

---

: расхождение во времени для одного измерения не должно превышать 0,2 с.

5. 6. По формуле (12) провести расчёт массы однородного шара. Заполнить таблицу.

Примечание. Всего 18 измерений времени (3 измерения времени на каждую высоту - массу). Сделать подробный вывод по проделанной работе.

Таблица

D, м		m, грузакг	h, м	t, с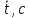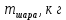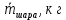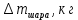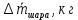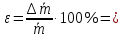

---

Вопросы для допуска

1. Поступательное и вращательное движение. Слоение движений твёрдого тела. Степени свободы.

2. Понятие момента силы. Момент силы относительно оси вращения. Пара сил.

3. Понятие момента инерции материальной точки и момента инерции твердого тела.

4. Основное уравнение динамики вращательного движения твердого тела около неподвижной оси. Понятие момента импульса. Свойства момента инерции.

5. Теорема Штейнера о параллельных осях (с доказательством).

6. Вычисление моментов инерции кольца (обруча), диска (сплошного цилиндра), стержня, шара – относительно оси проходящей через центр масс.

7. Теорема о моменте инерции плоских тел (с доказательством).

8. Полная кинетическая энергия движущегося тела.

9. Закон сохранения момента импульса тела.

10. Вывод расчётной формулы. Методика выполнения работы.

Вопросы для защиты

Решение задачи на тему динамики вращательного движения.

---

ЛАБОРАТОРНАЯ РАБОТА № 8

Определение момента инерции маховика динамическим методом

Ц 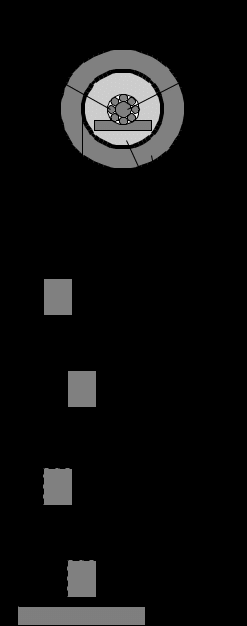ель работы: изучение свойств момента инерции; опытное определение момента инерции маховика относительно оси вращения.

Приборы и принадлежности: маховик, капроновая нить, грузы (2 груза разной массы), платформа, технические весы, сантиметровая линейка, механический секундомер, штангенциркуль.

Введение

Если к телу, которое может вращаться около неподвижной оси, приложен вращающий момент относительно данной оси, то под его действием тело получает упругое угловое ускорение, то есть начинает вращаться. При этом вращающий момент M и угловое ускорение , связаны соотношением:

, (1)

где I – момент инерции тела относительно оси вращения, характеризует инертность тела во вращательном движении.

Момент инерции тела относительно данной оси вращения рассчитывается по формуле:

,

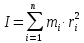где m_i – масса i-той материальной точки тела, r_i– расстояние i-той материальной точки от оси вращения.

Если к телу приложен вращающий момент M, величина которого в процессе вращения остается постоянной, то вращение тела будет равноускоренным. Наблюдая равноускоренное вращение тела, под действием постоянного момента, и измеряя соответствующим образом угловое ускорение , можно определить момент инерции тела относительно оси вращения:

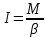. (2)

Описание установки и метода измерения. Маховик 1 (смотрите рисунок) жестко укреплен на валу 2. Вал может вращаться в подшипниках 3 с малым трением около горизонтальной оси. Ось вращения проходит через центр тяжести маховика. На валу маховика также жестко закреплены два плексигласовых шкива 4 различных диаметров. В одном из шкивов имеется маленькое отверстие для продевания капроновой нити 5; нить наматывается в несколько оборотов на один из шкивов. На свободный конец нити подвешивается груз

---

P, приводящий всю систему в равноускоренное движение. Также крепится сантиметровая линейка 6 (на данном рисунке отсутствует).

Под действием груза P на маховик будет действовать вращающий момент M, равный произведению силы натяжения нити F на плечо 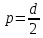, то есть:

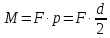, (3)

где d – диаметр шкива 4.

Если груз действует на нить с силой P, то нить действует на груз с силой F и в соответствии с третьим законом Ньютона эти силы равны по величине (и противоположны по направлению), то есть:

. (4)

Для определения силы F рассмотрим движение груза вниз. На груз действуют две силы: со стороны Земли - (вес груза ), и со стороны нити . Под действием этих сил груз будет двигаться равноускоренно с ускорением .Согласно второму закону Ньютона имеем: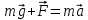

, (5)

где m – масса груза. Отсюда, в проекции на вертикальную координатную ось, получим:

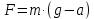, (6)

где g – ускорение силы тяжести.

Вращающий момент M с учетом (4) и (6) определяется выражением

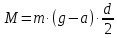,. (7)

Тогда, момент инерции маховика на основании уравнения (2), равен:

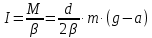, (8)

где  – угловое ускорение маховика и шкива. Угловое ускорение шкива  и тангенциальное ускорение точек, лежащих на его ободе, связаны следующим образом:

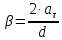. (9)

Понятно, что тангенциальное ускорение с которым вращаются точки лежащие на ободе шкива (нить, накручена на шкив) и линейное ускорение a с которым опускается груз равны ( ).

Величину линейного ускорения

---