Файл: Методические указания к лабораторным работам для студентов специальности 140101.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 160
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
причем зафиксируем этот адрес, нажав клавишу F4. В третьей ячейке с именем Стандартное_откл укажем фиксированный адрес среднеквадратичного отклонения N$5$. В четвертой ячейке с именем Интегральная укажем логическое значение Истина, указывающее, что функция НОРМРАСП должна вычислить интегральную характеристику. После ввода параметров нажмем клавишу ОК, после чего в ячейке В8 будет выведено значение интегральной функции нормального распределения, соответствующее введенным параметрам.
Растянем эту ячейку до J8, определив тем самым функцию распределения для первых девяти интервалов. В последний интервал должны попасть все возможные значения случайной величины больше верхней границы предпоследнего интервала, поэтому функция распределения для этого интервала должна быть равной единице. Введем в ячейку К8 число 1.
Вероятность попадания случайной величины в первый интервал равна функции распределения для этого интервала, вероятность попадания в другие интервалы равна разности функций распределения данного и предыдущего интервалов. Введем в ячейку В9 значение функции из ячейки В8, а в ячейке С9 запишем формулу =C8-B8 и растянем ячейку до К9.
Для расчета критерия Пирсона подсчитаем теоретическое количество попаданий случайной величины в интервалы. Введем в ячейку А10 заголовок строки np, запишем в ячейку В10 формулу =B9*60 и растянем эту ячейку до К10.
Вычислим слагаемые в критерии Пирсона. В ячейке А11 запишем заголовок строки (m-np)^2/np, введем в ячейку В11 формулу
=(B6-B10)^2/B10 и растянем ее до К11. Далее в ячейке М7 запишем заголовок критерия х2 и в ячейку N7 введем формулу =СУММ(B11:K11).
Найдем вероятность р появления числа χ2, большего наблюдаемого. В ячейке М8 запишем заголовок, активизируем ячейку N8 и с помощью Мастера функций из раздела статистические вызовем функцию ХИ2РАСП. На экране появится меню функции, в которое надо ввести два аргумента. В качестве параметра х укажем ячейку N7, в которой хранится значение критерия Пирсона. Вторым параметром является число степеней свободы. В нашем примере опытные данные были сгруппированы по 10 интервалам. На основании этих данных были определены два параметра распределения m и . Таким образом, на опытные данные наложены три связи: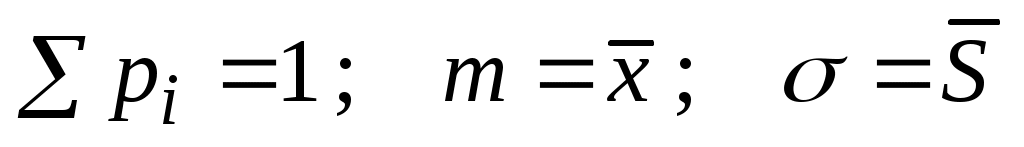
. Согласно формуле (2.6) общее количество степеней свободы составит 10 - 3 =7. Введем в качестве второго параметра число 7 и нажмем клавишу ОК. В ячейке N8 появится значение вероятности.
В нашем случае оказалось р = 0,6408. Так как данная вероятность малой не является, поэтому гипотезу о том, что разброс результатов подчиняется нормальному закону, можно считать правдоподобной. Этот вывод запишем в ячейке А13.
Общий вид рабочего листа лабораторной работы №2 показан на рис. 2.2.
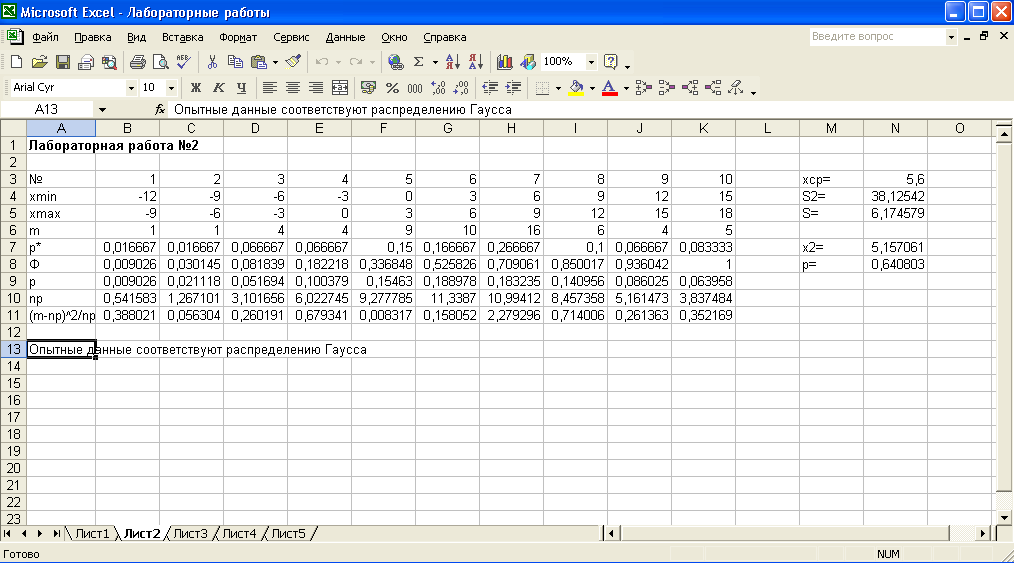
Рис. 2.2. Общий вид рабочего листа лабораторной работы №2
Лабораторная работа №3
Статистическая обработка
результатов параллельных измерений
Ближайшей задачей экспериментатора является получение интересующих результатов с заданной точностью. Однако данные, полученные непосредственно считыванием с приборов во время проведения опытов или косвенно путем пересчета опытных значений, могут содержать различные по своей природе ошибки, вносящие некоторую погрешность в окончательный результат. В дальнейшем будем предполагать, что первичные данные могут содержать только случайные ошибки и грубые промахи, систематические ошибки отсутствуют.
Случайные ошибки вызываются большим числом случайных факторов, действие которых в каждом измерении различно и не может быть заранее учтено. Предполагается, что влияние случайных факторов на результат складывается таким образом, что равновероятно получение одинаковых по абсолютной величине положительных и отрицательных отклонений от истинного значения наблюдаемой величины. В этом случае при повторении измерений при тех же видимых условиях значения исследуемой величины должны с некоторым разбросом группироваться около истинного значения. С увеличением количества измерений n среднее арифметическое результатов будет сходиться по вероятности к математическому ожиданию mx (истинному значению) исследуемого параметра, при этом среднее арифметическое, рассчитываемое по формуле
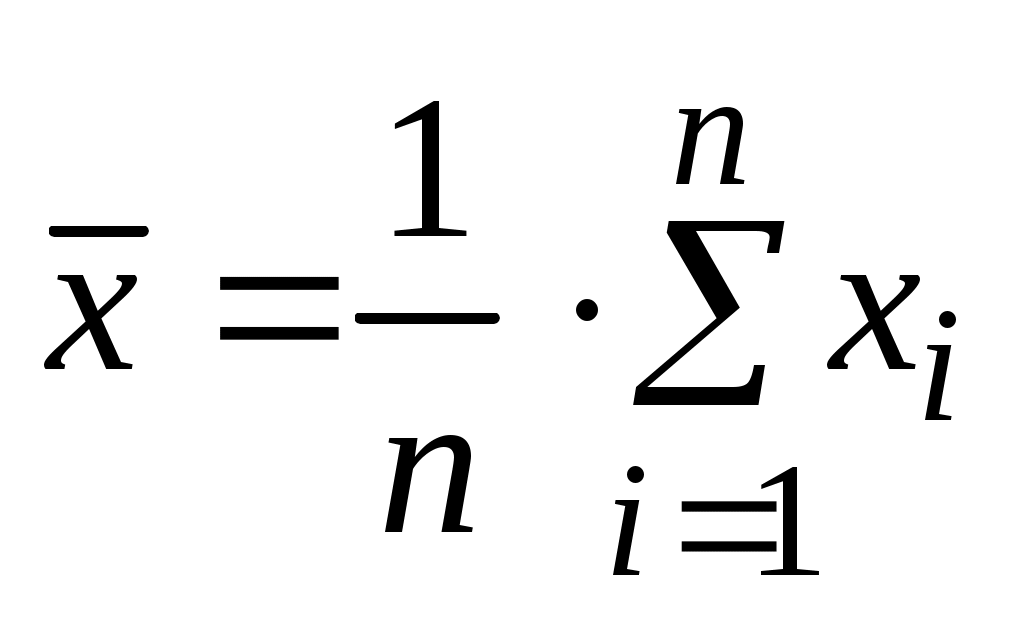, (3.1)
может рассматриваться в качестве оценочного (приближенного) значения истинной величины.
Разброс экспериментальных данных относительно среднего, характерный для данной серии измерений, определяется дисперсией:
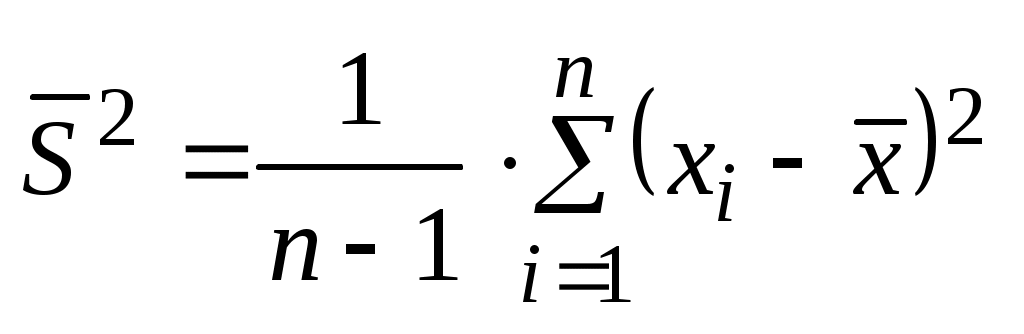(3.2)
или среднеквадратичным отклонением
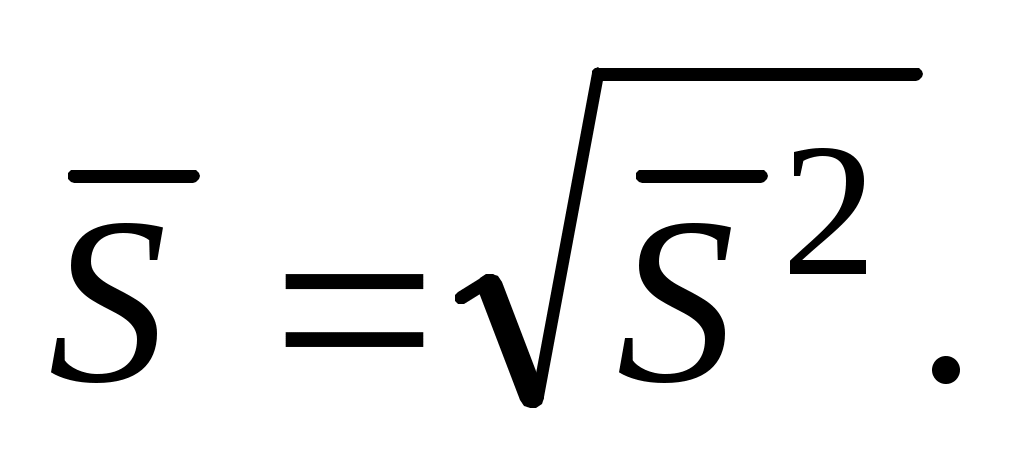(3.3)
Относительная изменчивость наблюдаемой случайной величины определяется коэффициентом вариации
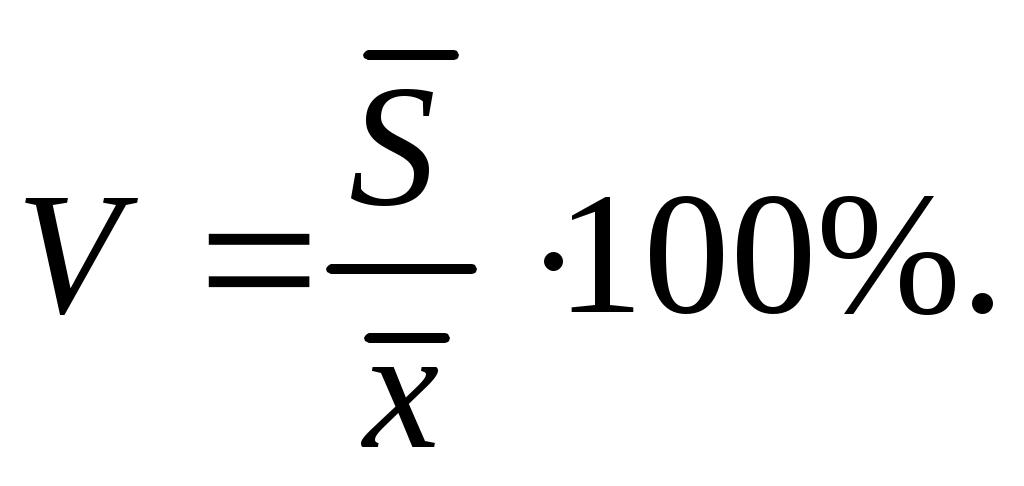(3.4)
Среднее арифметическое результатов, рассчитанное по (3.1), дает лишь приближенное значение измеряемого параметра. Его истинное значение находится в некоторой области, включающей при отсутствии систематических ошибок и грубых промахов точку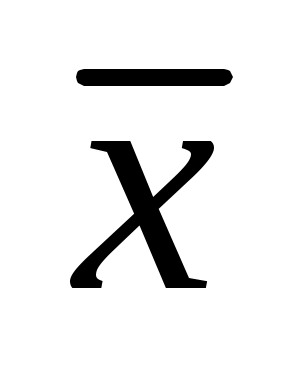
. Более информативной наряду с точечной оценкой 
дает оценка доверительного интервала
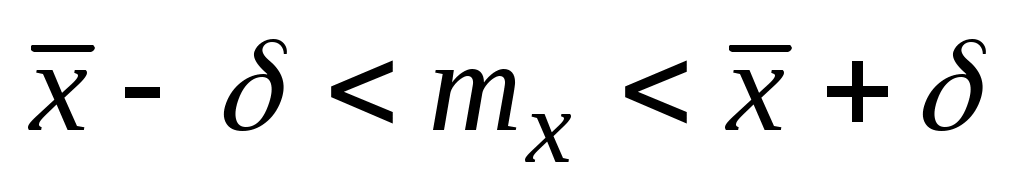, (3.5)
который с доверительной вероятностью β накрывает оцениваемый параметр mx.
Вероятность риска, что исследуемая величина находится вне доверительного интервала, в этом случае равна уровню значимости:
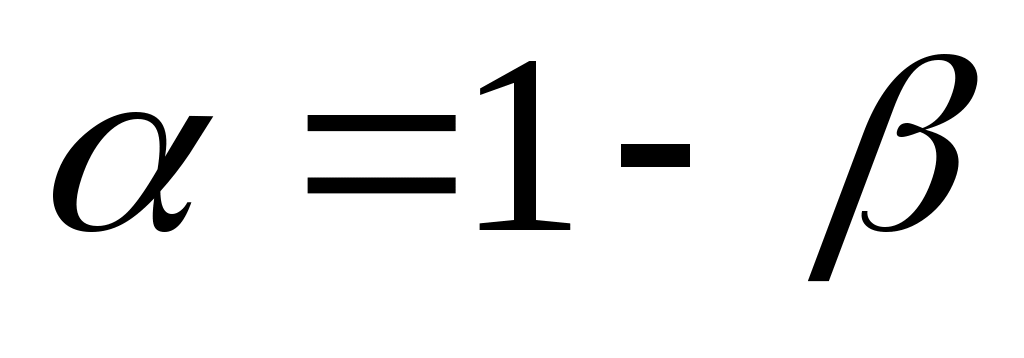. (3.6)
Принимая, что равновероятно появление одинаковых по абсолютной величине положительных и отрицательных отклонений, вероятности выхода величины х за нижнюю и верхнюю границы доверительного интервала (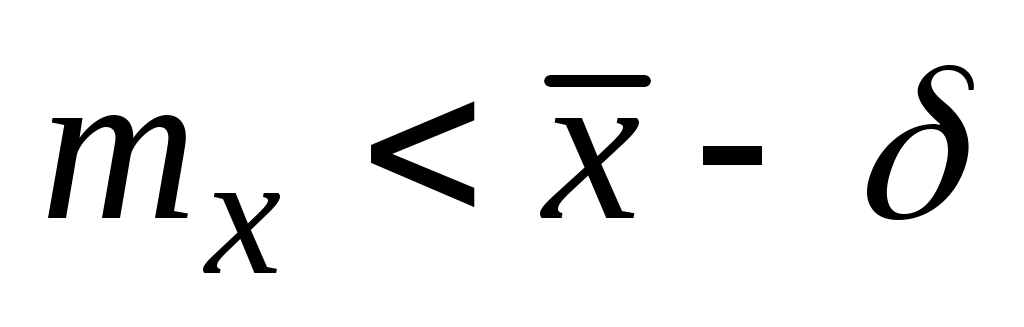
и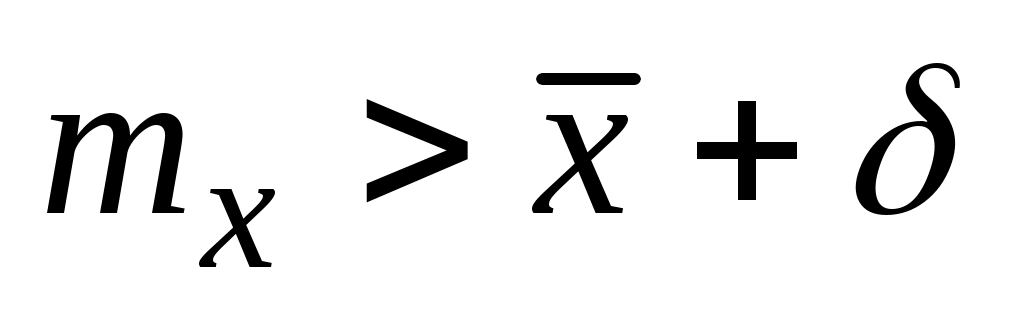 
) будут равны /2.
При отсутствии промахов и систематических погрешностей отклонение среднего арифметического от математического ожидания подчиняется распределению Стьюдента, параметром которого является величина
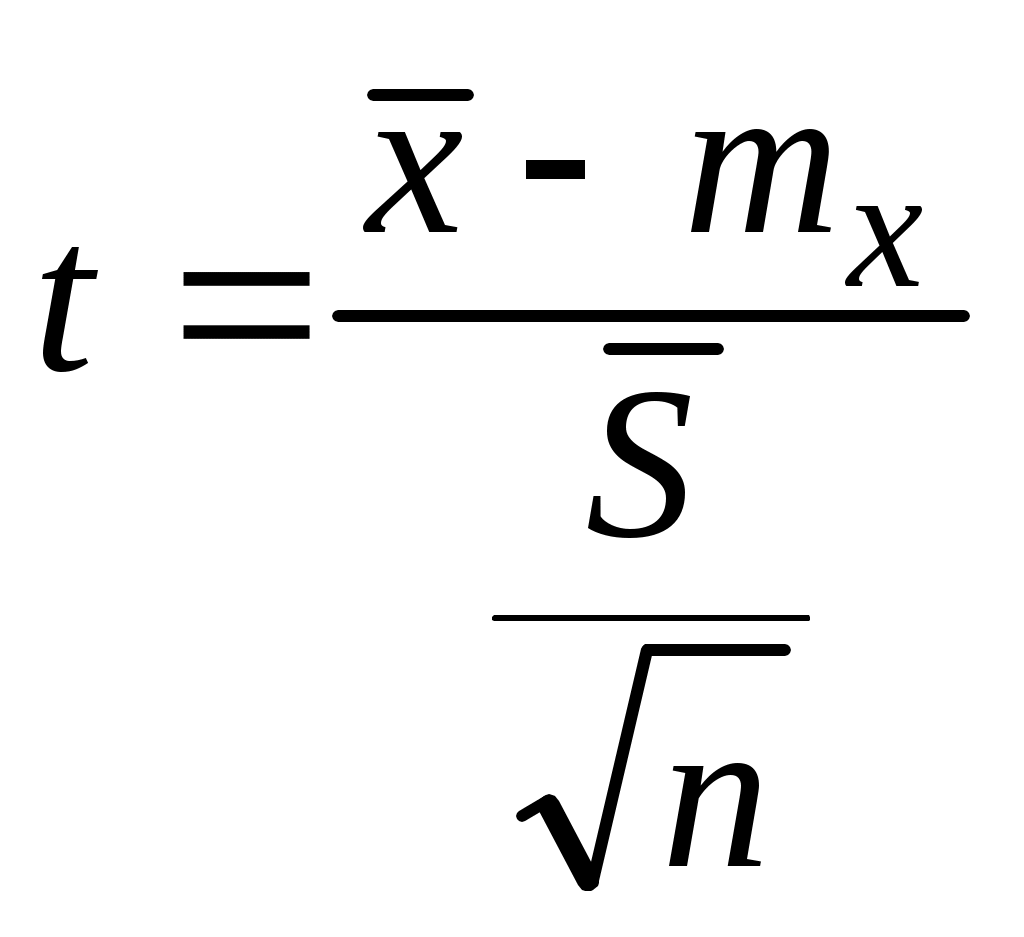. (3.7)
Для распределения Стьюдента составлены таблицы, связывающие значения параметра tкр и вероятность появления t, большего по абсолютной величине значения tкр. Задаваясь этой вероятностью (уровнем значимости), из (3.6) можно по tкр определить величину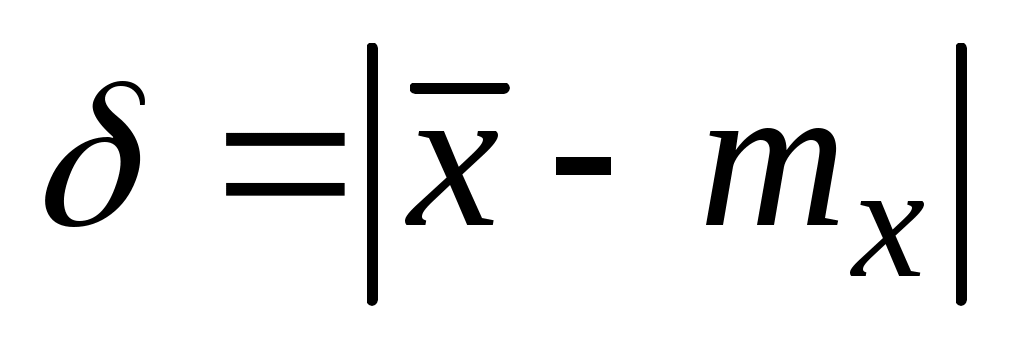
:
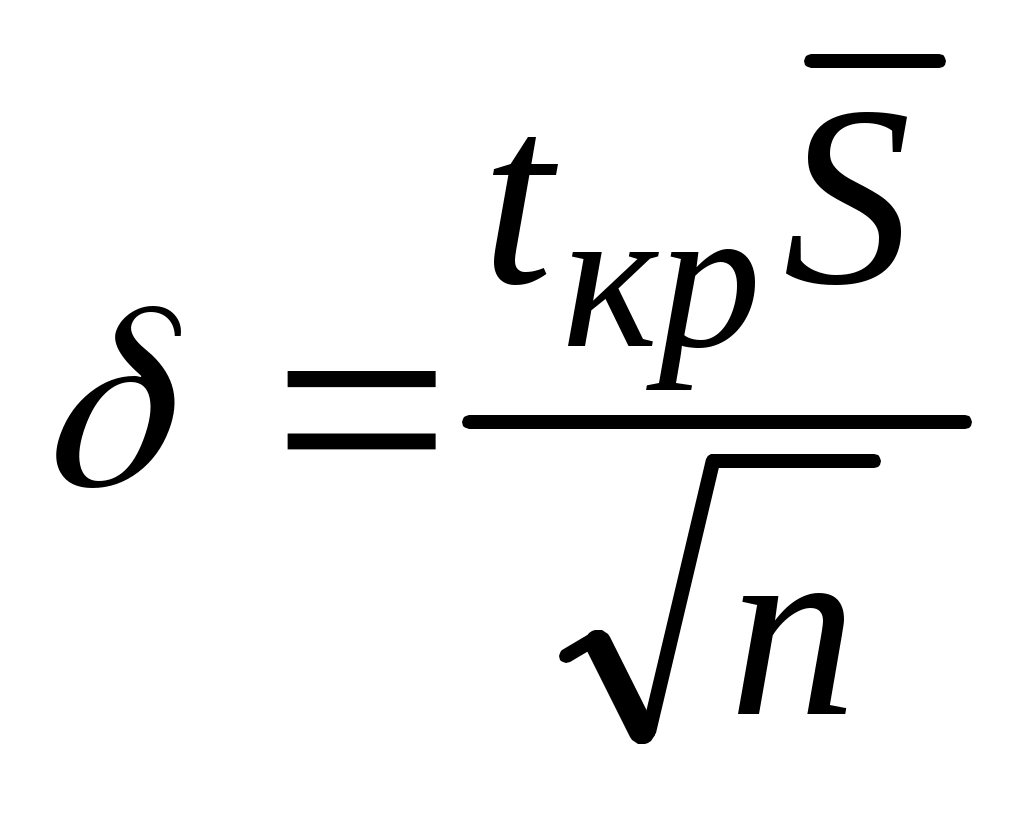, (3.8)
где параметр tкр определяется по числу степеней свободы ν = n - 1 и уровню значимости . Значения tкр приведены в табл. П 2.2. Параметр tкр можно также найти, используя функцию EXCELСТЬЮДРАСПОБР, указав величины ν и α.
Грубые промахи могут появиться вследствие ошибок экспериментатора, выхода из строя измерительной аппаратуры, нарушения режима работы установки и т.д. Признаком ошибок такого рода является несоответствие наблюдаемых значений с физической сущностью исследуемого процесса (несоответствие полученных характеристик агрегатному состоянию вещества, нарушение законов сохранения массы, энергии, количества движения и т.д.) или значительное отклонение данных от их среднего значения. При усреднении экспериментальных данных грубые промахи могут существенно исказить конечный результат, поэтому они должны быть исключены из совокупности обрабатываемых значений.
В первом случае отбраковка ошибочных результатов производится на основании тщательного анализа режима работы исследуемой установки: оценки с точки зрения физической сущности процесса допустимого диапазона ожидаемых результатов и соблюдения с заданной точностью законов сохранения. При выявленных нарушениях сомнительные измерения отбрасываются независимо от их величины. В данной работе будем считать, что отсев ошибочных результатов по этим признакам уже проведен.
Во втором случае на грубую ошибку указывает существенное отклонение одного или нескольких значений от общей массы результатов. Вопрос о том, насколько существенным должно быть отклонение результата от среднего значения, чтобы его считать грубой ошибкой, является в некоторой степени предметом соглашения о вероятности ошибки, с которой данный результат признается грубым промахом и исключается из анализируемой совокупности.
Для отбраковки грубых промахов t-распределение Стьюдента преобразуется в r-распределение. Параметром этого распределения является величина
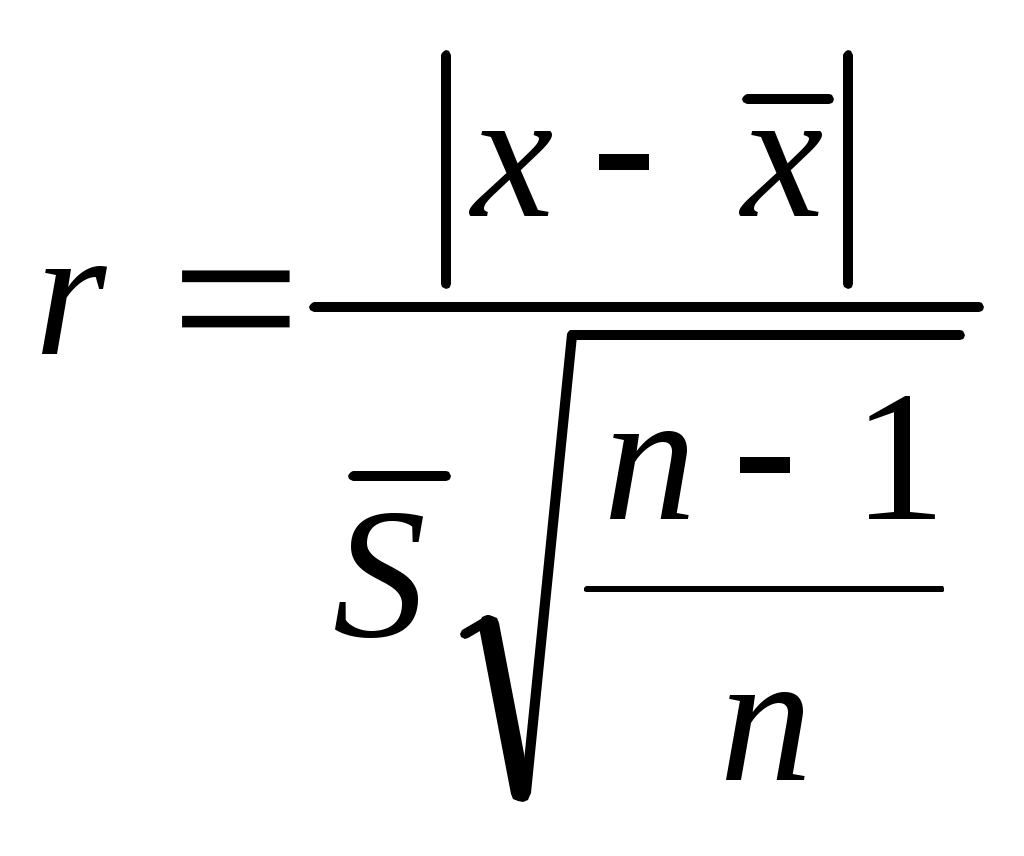. (3.9)
Если с заданной степенью доверительной вероятности β = 1 - α величина r попадает в доверительный интервал, то нет основания считать величину x грубым промахом и ее следует оставить в ряду результатов. В противном случае с вероятностью β можно признать, что величина
x попала в этот ряд из-за грубой ошибки и ее следует исключить. Вероятность ошибки исключения равна α.
Проверку на наличие промахов следует начинать со значения x, имеющего наибольшее отклонение по модулю от среднего значения. В табл. П 2.1 приведены численные значения r-распределения для различных уровней значимости и степеней свободы = n - 2. Если найденное значение r для максимального отклонения не превосходит по абсолютной величине табличного значения rкр для выбранного уровня значимости, то можно принять, что все измерения, по которым рассчитывались среднее арифметическое и дисперсия, образуют совокупность данных, для которой отклонения значений от среднего арифметического можно объяснить только влиянием случайных факторов, и ни один из результатов не является грубым промахом. В противном случае при r > rкр с вероятностью ошибки данный результат признается промахом и бракуется.
Если величина x с максимальным отклонением будет исключена из совокупности результатов эксперимента, то изменится среднее значение и среднеквадратичное отклонение . Поэтому необходим повторный пересчет этих значений.
Обычно обработку результатов параллельных измерений проводят в следующей последовательности:
- определяются величины отклонений результатов от среднего:
;
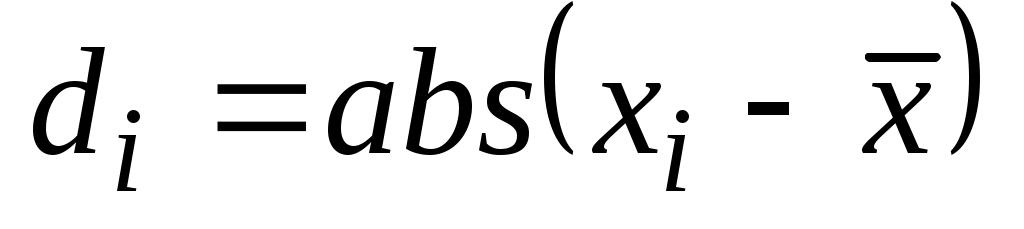– выбирается результат с максимальным di;
– по (3.9) для него рассчитывается величина ri;
– задается величина уровня значимости для выявления грубых промахов. В технических расчетах обычно принимают = 0,05;
– по числу степеней свободы ν = n- 2 и принятому из табл.
П 2.1. находят критическое число
Растянем эту ячейку до J8, определив тем самым функцию распределения для первых девяти интервалов. В последний интервал должны попасть все возможные значения случайной величины больше верхней границы предпоследнего интервала, поэтому функция распределения для этого интервала должна быть равной единице. Введем в ячейку К8 число 1.
Вероятность попадания случайной величины в первый интервал равна функции распределения для этого интервала, вероятность попадания в другие интервалы равна разности функций распределения данного и предыдущего интервалов. Введем в ячейку В9 значение функции из ячейки В8, а в ячейке С9 запишем формулу =C8-B8 и растянем ячейку до К9.
Для расчета критерия Пирсона подсчитаем теоретическое количество попаданий случайной величины в интервалы. Введем в ячейку А10 заголовок строки np, запишем в ячейку В10 формулу =B9*60 и растянем эту ячейку до К10.
Вычислим слагаемые в критерии Пирсона. В ячейке А11 запишем заголовок строки (m-np)^2/np, введем в ячейку В11 формулу
=(B6-B10)^2/B10 и растянем ее до К11. Далее в ячейке М7 запишем заголовок критерия х2 и в ячейку N7 введем формулу =СУММ(B11:K11).
Найдем вероятность р появления числа χ2, большего наблюдаемого. В ячейке М8 запишем заголовок, активизируем ячейку N8 и с помощью Мастера функций из раздела статистические вызовем функцию ХИ2РАСП. На экране появится меню функции, в которое надо ввести два аргумента. В качестве параметра х укажем ячейку N7, в которой хранится значение критерия Пирсона. Вторым параметром является число степеней свободы. В нашем примере опытные данные были сгруппированы по 10 интервалам. На основании этих данных были определены два параметра распределения m и . Таким образом, на опытные данные наложены три связи:
. Согласно формуле (2.6) общее количество степеней свободы составит 10 - 3 =7. Введем в качестве второго параметра число 7 и нажмем клавишу ОК. В ячейке N8 появится значение вероятности.
В нашем случае оказалось р = 0,6408. Так как данная вероятность малой не является, поэтому гипотезу о том, что разброс результатов подчиняется нормальному закону, можно считать правдоподобной. Этот вывод запишем в ячейке А13.
Общий вид рабочего листа лабораторной работы №2 показан на рис. 2.2.
Рис. 2.2. Общий вид рабочего листа лабораторной работы №2
Лабораторная работа №3
Статистическая обработка
результатов параллельных измерений
Ближайшей задачей экспериментатора является получение интересующих результатов с заданной точностью. Однако данные, полученные непосредственно считыванием с приборов во время проведения опытов или косвенно путем пересчета опытных значений, могут содержать различные по своей природе ошибки, вносящие некоторую погрешность в окончательный результат. В дальнейшем будем предполагать, что первичные данные могут содержать только случайные ошибки и грубые промахи, систематические ошибки отсутствуют.
Случайные ошибки вызываются большим числом случайных факторов, действие которых в каждом измерении различно и не может быть заранее учтено. Предполагается, что влияние случайных факторов на результат складывается таким образом, что равновероятно получение одинаковых по абсолютной величине положительных и отрицательных отклонений от истинного значения наблюдаемой величины. В этом случае при повторении измерений при тех же видимых условиях значения исследуемой величины должны с некоторым разбросом группироваться около истинного значения. С увеличением количества измерений n среднее арифметическое результатов будет сходиться по вероятности к математическому ожиданию mx (истинному значению) исследуемого параметра, при этом среднее арифметическое, рассчитываемое по формуле
, (3.1)может рассматриваться в качестве оценочного (приближенного) значения истинной величины.
Разброс экспериментальных данных относительно среднего, характерный для данной серии измерений, определяется дисперсией:
(3.2)или среднеквадратичным отклонением
(3.3)Относительная изменчивость наблюдаемой случайной величины определяется коэффициентом вариации
(3.4)Среднее арифметическое результатов, рассчитанное по (3.1), дает лишь приближенное значение измеряемого параметра. Его истинное значение находится в некоторой области, включающей при отсутствии систематических ошибок и грубых промахов точку
. Более информативной наряду с точечной оценкой дает оценка доверительного интервала , (3.5)который с доверительной вероятностью β накрывает оцениваемый параметр mx.
Вероятность риска, что исследуемая величина находится вне доверительного интервала, в этом случае равна уровню значимости:
. (3.6)Принимая, что равновероятно появление одинаковых по абсолютной величине положительных и отрицательных отклонений, вероятности выхода величины х за нижнюю и верхнюю границы доверительного интервала (
и ) будут равны /2.При отсутствии промахов и систематических погрешностей отклонение среднего арифметического от математического ожидания подчиняется распределению Стьюдента, параметром которого является величина
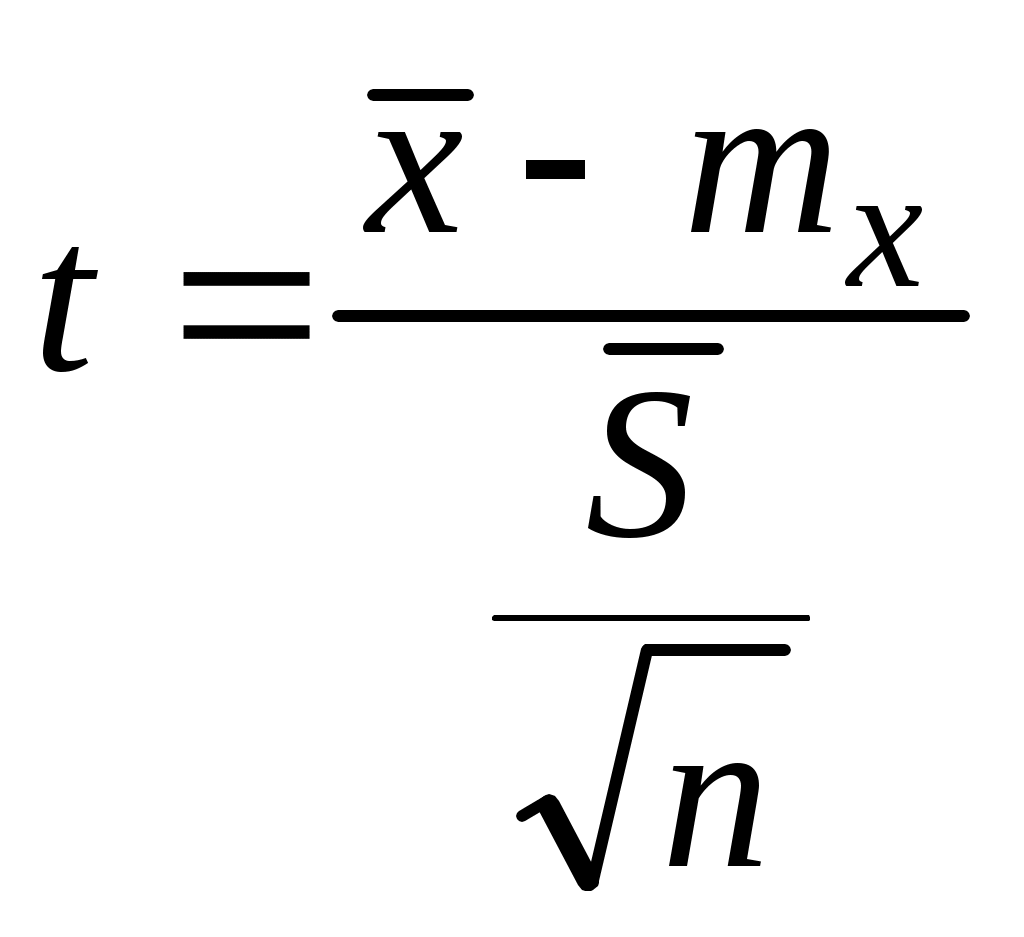. (3.7)Для распределения Стьюдента составлены таблицы, связывающие значения параметра tкр и вероятность появления t, большего по абсолютной величине значения tкр. Задаваясь этой вероятностью (уровнем значимости), из (3.6) можно по tкр определить величину
:
, (3.8)где параметр tкр определяется по числу степеней свободы ν = n - 1 и уровню значимости . Значения tкр приведены в табл. П 2.2. Параметр tкр можно также найти, используя функцию EXCELСТЬЮДРАСПОБР, указав величины ν и α.
Грубые промахи могут появиться вследствие ошибок экспериментатора, выхода из строя измерительной аппаратуры, нарушения режима работы установки и т.д. Признаком ошибок такого рода является несоответствие наблюдаемых значений с физической сущностью исследуемого процесса (несоответствие полученных характеристик агрегатному состоянию вещества, нарушение законов сохранения массы, энергии, количества движения и т.д.) или значительное отклонение данных от их среднего значения. При усреднении экспериментальных данных грубые промахи могут существенно исказить конечный результат, поэтому они должны быть исключены из совокупности обрабатываемых значений.
В первом случае отбраковка ошибочных результатов производится на основании тщательного анализа режима работы исследуемой установки: оценки с точки зрения физической сущности процесса допустимого диапазона ожидаемых результатов и соблюдения с заданной точностью законов сохранения. При выявленных нарушениях сомнительные измерения отбрасываются независимо от их величины. В данной работе будем считать, что отсев ошибочных результатов по этим признакам уже проведен.
Во втором случае на грубую ошибку указывает существенное отклонение одного или нескольких значений от общей массы результатов. Вопрос о том, насколько существенным должно быть отклонение результата от среднего значения, чтобы его считать грубой ошибкой, является в некоторой степени предметом соглашения о вероятности ошибки, с которой данный результат признается грубым промахом и исключается из анализируемой совокупности.
Для отбраковки грубых промахов t-распределение Стьюдента преобразуется в r-распределение. Параметром этого распределения является величина
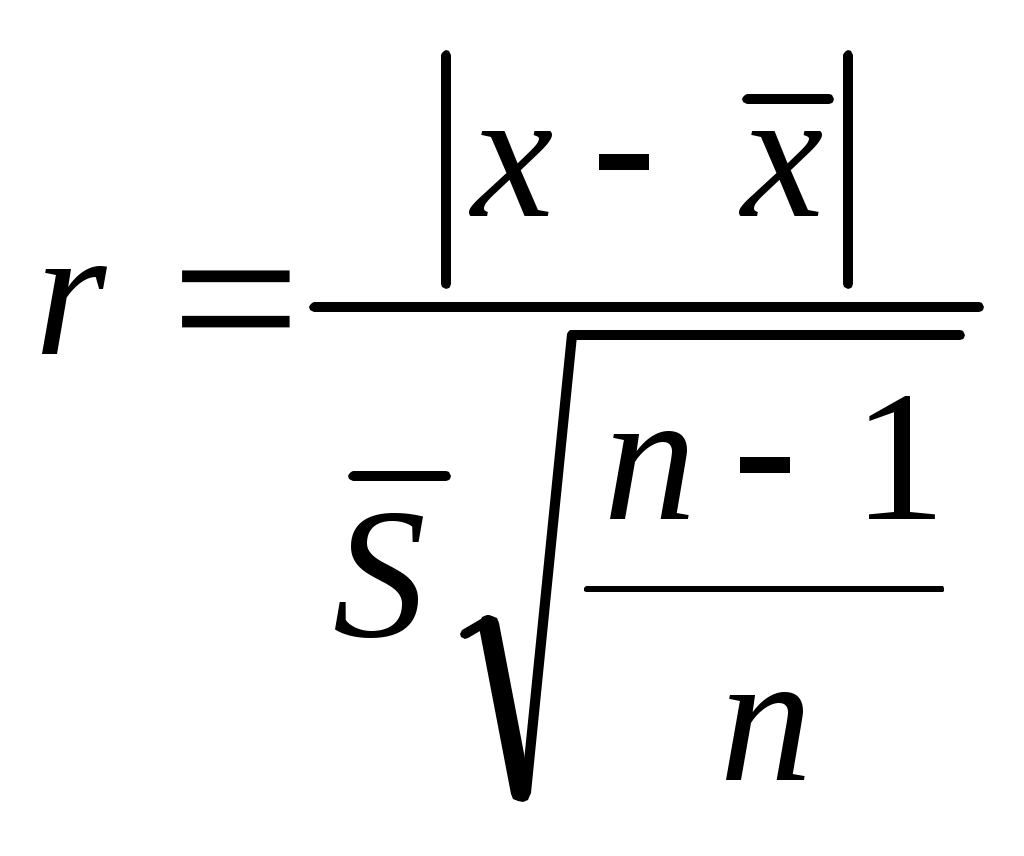. (3.9)Если с заданной степенью доверительной вероятности β = 1 - α величина r попадает в доверительный интервал, то нет основания считать величину x грубым промахом и ее следует оставить в ряду результатов. В противном случае с вероятностью β можно признать, что величина
x попала в этот ряд из-за грубой ошибки и ее следует исключить. Вероятность ошибки исключения равна α.
Проверку на наличие промахов следует начинать со значения x, имеющего наибольшее отклонение по модулю от среднего значения. В табл. П 2.1 приведены численные значения r-распределения для различных уровней значимости и степеней свободы = n - 2. Если найденное значение r для максимального отклонения не превосходит по абсолютной величине табличного значения rкр для выбранного уровня значимости, то можно принять, что все измерения, по которым рассчитывались среднее арифметическое и дисперсия, образуют совокупность данных, для которой отклонения значений от среднего арифметического можно объяснить только влиянием случайных факторов, и ни один из результатов не является грубым промахом. В противном случае при r > rкр с вероятностью ошибки данный результат признается промахом и бракуется.
Если величина x с максимальным отклонением будет исключена из совокупности результатов эксперимента, то изменится среднее значение и среднеквадратичное отклонение . Поэтому необходим повторный пересчет этих значений.
Обычно обработку результатов параллельных измерений проводят в следующей последовательности:
-
Производится анализ первичных данных и из совокупности исключаются результаты, противоречащие физической сущности процесса, полученные при нарушении режима работы исследуемого объекта или при неисправной измерительной системе. -
По (3.1) – (3.3) вычисляют среднее арифметическое результатов , дисперсию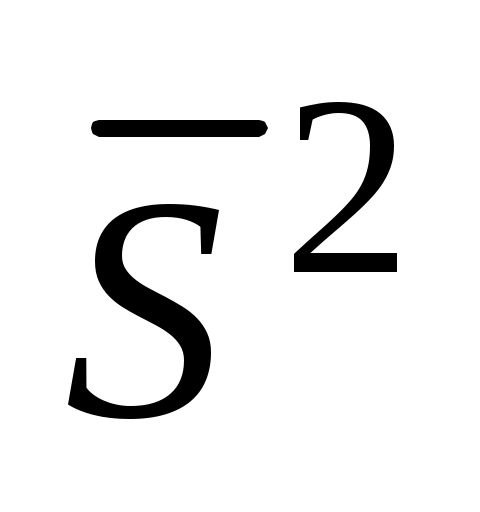 
и среднеквадратичное отклонение 
. -
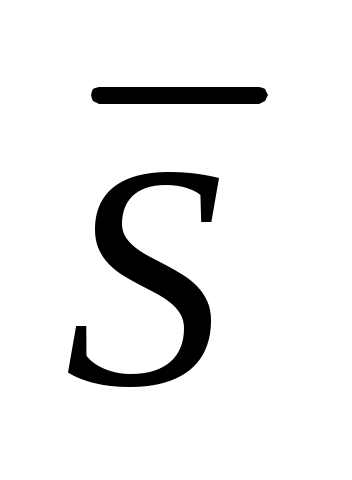Производится отсев грубых промахов, для чего:
- определяются величины отклонений результатов от среднего:
;– выбирается результат с максимальным di;
– по (3.9) для него рассчитывается величина ri;
– задается величина уровня значимости для выявления грубых промахов. В технических расчетах обычно принимают = 0,05;
– по числу степеней свободы ν = n- 2 и принятому из табл.
П 2.1. находят критическое число