ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 39
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= 0,85 моль/дм3;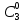 
= 0,5 моль/дм3; 
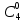= 0,25 моль/дм3. На рис. 1, показано как определить 
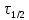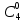для = 0,2 моль/дм3. Для этого из ординаты 
= 0,3 моль/дм3 проводят линию, параллельную оси абсцисс до пересечения с кривой. Аналогичную линию проводят из ординаты /2 = 0,15 моль/дм3 . Период полупревращения 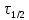определяют из выражения:
= 
– 
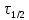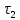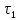= 190 – 42 = 148 с.
Определив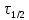 для всех концентраций, сведем данные в табл. 5.
Таблица 5
Период полупревращения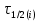
при различных исходных концентрациях
Период полупревращения связан с порядком реакции уравнением:
= 
·
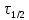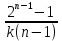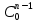
(5)
Обозначив отношение
= B и прологарифмировав (5), получим:
= lg B + (1 – n) lg 
(6)
Выражение (6) является уравнением прямой в координатах lg – lg . Построим эту прямую на рис.3 и определим порядок из уравнения:
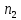= 1 – tg α (7)
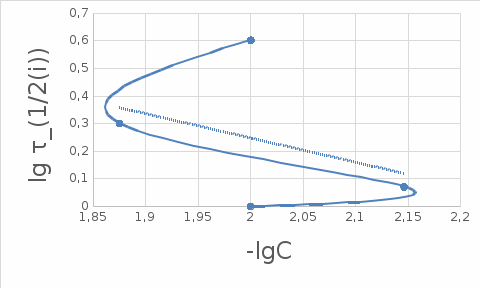
Рисунок 3 Зависимость десятичного логарифма периода полупревращения от исходной концентрации
Определяем из рис. 3 тангенс угла наклона прямой tg α:
tg α =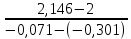
= 0,635
Из уравнения (7) определим порядок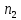 = 1 – ( 0,635) = 0,365
Поскольку порядки, найденные разными способами различны, то истинный порядок определяем как среднее между двумя значениями:
n =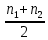
= 
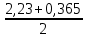
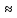1,297
Подставив в уравнение (1) найденный порядок реакции, определим вид кинетического уравнения:
kτ =
kτ = 
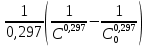(8)
По уравнению (8), зная исходные концентрации и текущие – 
в момент 
, можно рассчитать константы скорости при требуемых температурах 
–
.
Значения исходных и текущих концентраций через 190 с от начала реакции возьмем из табл.3.
= 
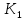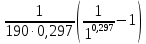= 0 
· 
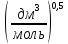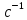( = 329 К)
= 
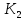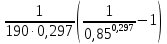= 4,76 · 10-3 · (
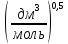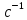= 331 К)
= 
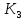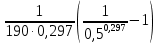= 9,2 · 10-3 · (
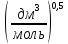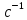= 333 К)
= 
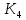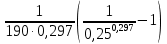= 13,7 · 10-3 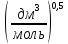· 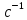( = 310 К)
Зависимость константы скорости k от температуры Т описывается основным уравнением химической кинетики (уравнением Аррениуса ):
k =
· 
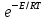(9)
где - предэкспоненциальный множитель;
е - основание натурального логарифма;
Е – энергия активации;
R – универсальная газовая постоянная.
В малом интервале температур (до 800 К ) величины
и Е изменяются незначительно и их можно считать постоянными. Это допущение дает возможность определить их значения графически. После логарифмирования уравнения (9):
ln k = ln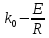
· 
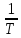(10)
Видно, что в координатах ln k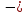
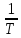график этой функции представляет собой прямую, тангенс угла наклона которой есть отношение Е/ R , т.е.
tg α =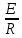
(11)
Для построения графика сведем ранее определенные данные в табл. 6.
Таблица 6
Значение константы скорости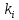
при различных температурах 
По данным таблицы 6 построена зависимость, представленная на рис.4.1.
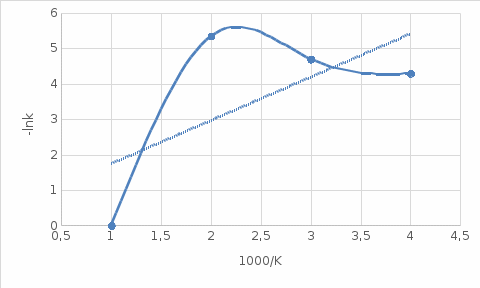
Рисунок 4. Зависимость логарифма константы скорости от обратной температуры
Из рис.4 определяем тангенс наклона:
tgα =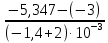
= – 5867,5
и затем из уравнения (11) энергию активации
E = -5867,5 · 8,31 = -48758,93 (Дж/моль)
Значение предэкспоненциального множителя найдем из уравнения (10), подставить в него любую пару значений ln
k и
, взятых из рис.4.
Например, при = 4,76*10-3; ln k = – 5,347.
Тогда: ln = ln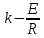 
· = – 5,347 + 
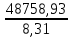· 4,76 · 10-3 = 22,58
Откуда = 
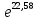= 5,49*109
Итак, все постоянные в уравнениях (9.10) известны. Находим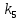
при 
= 330 К.
ln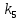 = -5,347 + · 
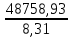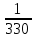= 13,58
= 
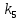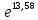= 7,209*105 
· 
Используя выражение (8) рассчитаем время, за которое 60% исходных веществ превратятся в продукты реакции, т.е. их концентрация изменится от значения = 1 моль/дм3 до значения С = 0,6 моль/дм3 при температуре 330 К.
τ =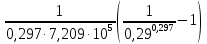
= 2,382*10-6 с
Таким образом, при температуре 330 К, при исходных концентрациях реагирующих веществ (А) = (В) = = 1 моль/дм3 60 % исходных веществ прореагирует за 2,382*10-6 с.
раздел «Адсорбция»
При адсорбции уксусной кислоты из 200 мл водного раствора на 4 г активированного угля при 20 0С получены следующие данные (табл. 7). Установить, каким из адсорбционных уравнений Фрейндлиха или Лэнгмюра описывается адсорбция в рассматриваемом случае. Найти постоянные в соответствующем уравнении, а также равновесную концентрацию раствора
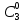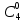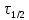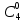= 0,5 моль/дм3; = 0,25 моль/дм3. На рис. 1, показано как определить для = 0,2 моль/дм3. Для этого из ординаты = 0,3 моль/дм3 проводят линию, параллельную оси абсцисс до пересечения с кривой. Аналогичную линию проводят из ординаты /2 = 0,15 моль/дм3 . Период полупревращения 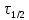определяют из выражения: 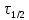= 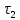– 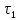= 190 – 42 = 148 с.Определив
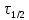для всех концентраций, сведем данные в табл. 5. Таблица 5
Период полупревращения
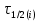при различных исходных концентрациях | , моль/дм3 | 1 | 0,85 | 0,5 | 0,25 |
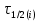| , с | 100 | 140 | 75 | 100 |
| – lg | 0 | 0,071 | 0,301 | 0,602 |
| lg 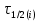| 2 | 2,146 | 1,875 | 2 |
Период полупревращения связан с порядком реакции уравнением:
= ·
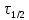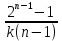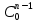
(5)
Обозначив отношение
= B и прологарифмировав (5), получим: = lg B + (1 – n) lg (6)Выражение (6) является уравнением прямой в координатах lg
– lg . Построим эту прямую на рис.3 и определим порядок из уравнения: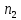 = 1 – tg α (7) Рисунок 3 Зависимость десятичного логарифма периода полупревращения
от исходной концентрации Определяем из рис. 3 тангенс угла наклона прямой tg α:
tg α =
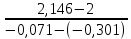= 0,635Из уравнения (7) определим порядок
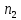= 1 – ( 0,635) = 0,365Поскольку порядки, найденные разными способами различны, то истинный порядок определяем как среднее между двумя значениями:
n =
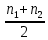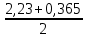
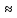= 1,297Подставив в уравнение (1) найденный порядок реакции, определим вид кинетического уравнения:
kτ =
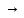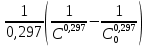kτ = (8)По уравнению (8), зная исходные концентрации
и текущие – в момент , можно рассчитать константы скорости при требуемых температурах
–
.Значения исходных и текущих концентраций через 190 с от начала реакции возьмем из табл.3.
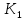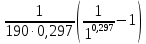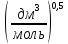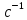= = 0 · ( = 329 К)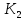 = = 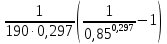4,76 · 10-3 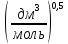· 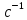( = 331 К)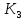 = = 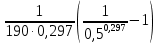9,2 · 10-3 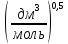· 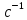( = 333 К)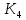 = = 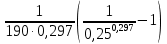13,7 · 10-3 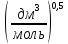· 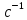( = 310 К)-
Определение энергии активации и предэкспоненциального множителя
Зависимость константы скорости k от температуры Т описывается основным уравнением химической кинетики (уравнением Аррениуса ):
k =
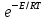· (9)где
- предэкспоненциальный множитель;е - основание натурального логарифма;
Е – энергия активации;
R – универсальная газовая постоянная.
В малом интервале температур (до 800 К ) величины
и Е изменяются незначительно и их можно считать постоянными. Это допущение дает возможность определить их значения графически. После логарифмирования уравнения (9):
ln k = ln
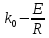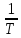· (10)Видно, что в координатах ln k
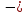
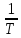график этой функции представляет собой прямую, тангенс угла наклона которой есть отношение Е/ R , т.е.tg α =
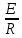(11)Для построения графика сведем ранее определенные данные в табл. 6.
Таблица 6
Значение константы скорости
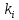при различных температурах | , К | 313 | 315 | 317 | 320 |
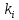| , · | 0 | 4,76*10-3 | 9,2*10-3 | 13,7*10-3 |
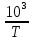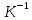 ,  | 3.04 | 3.02 | 3.003 | 2,958 |
| – ln 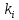| 0 | 5,347 | 4,688 | 4,29 |
По данным таблицы 6 построена зависимость, представленная на рис.4.1.
Рисунок 4. Зависимость логарифма константы скорости от обратной температуры
Из рис.4 определяем тангенс наклона:
tgα =
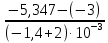= – 5867,5и затем из уравнения (11) энергию активации
E = -5867,5 · 8,31 = -48758,93 (Дж/моль)
Значение предэкспоненциального множителя найдем из уравнения (10), подставить в него любую пару значений ln
k и
, взятых из рис.4.Например, при
= 4,76*10-3; ln k = – 5,347.Тогда: ln
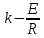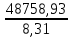= ln · = – 5,347 + · 4,76 · 10-3 = 22,58Откуда
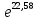= = 5,49*109Итак, все постоянные в уравнениях (9.10) известны. Находим
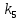при = 330 К.ln
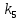= -5,347 + 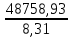· 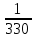= 13,58 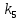= = 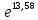7,209*105 · Используя выражение (8) рассчитаем время, за которое 60% исходных веществ превратятся в продукты реакции, т.е. их концентрация изменится от значения
= 1 моль/дм3 до значения С = 0,6 моль/дм3 при температуре 330 К.τ =
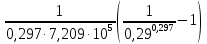= 2,382*10-6 сТаким образом, при температуре 330 К, при исходных концентрациях реагирующих веществ
(А) = (В) = = 1 моль/дм3 60 % исходных веществ прореагирует за 2,382*10-6 с.-
ИССЛЕДОВАНИЕ 2
раздел «Адсорбция»
При адсорбции уксусной кислоты из 200 мл водного раствора на 4 г активированного угля при 20 0С получены следующие данные (табл. 7). Установить, каким из адсорбционных уравнений Фрейндлиха или Лэнгмюра описывается адсорбция в рассматриваемом случае. Найти постоянные в соответствующем уравнении, а также равновесную концентрацию раствора