Файл: Задача 1 14 1,1 6,9 19 1,1 19 4890 19 34,1 19 390 19 1,4 19 4020 19 27,7 19 1489 19 1,6 19 11960 19.docx
Добавлен: 06.11.2023
Просмотров: 43
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Комбинационная таблица по стоимости ОПФ и численности персонала.
| Группы предприятий по стоимости ОПФ | Подгруппы по численности персонала | Итого | ||
| 25 – 73 | 74 – 121 | 122 - 69 | ||
| Объем производства продукции, тыс. шт. | ||||
| 82 – 102 | 7678,9 | 6861,3 | 4020,0 | 7183,9 |
| 103 – 108 | 8436,7 | 4702,5 | 15895,0 | 8435,6 |
| 109 – 116 | 8445,0 | 14410,0 | 6500,0 | 9450,0 |
| 116 – 124 | 8900,0 | 9600,0 | 16500,0 | 11666,7 |
Анализ полученной таблицы позволяет сделать следующие выводы.
Средние значения результативного признака объема производства в последнем столбце увеличиваются, т.е. между стоимостью ОПФ и объемом производства прослеживается четко выраженная связь. Сравнивая средние значения выпуска продукции по каждой подгруппе, замечаем, что тенденция к росту наблюдается только для 4-й группы. Отсюда можно предположить, что связи между численностью персонала и объемом производства не прослеживается.
Задача 4
Построить аналитическую группировку предприятий табачной промышленности, характеризующую зависимость объема производства табачных изделий от влияния стоимости основных производственных фондов. Результаты изложите в табличной форме и проанализируйте их.
Решение: Используя результаты, полученные при решении 2-й задачи, построим аналитическую группировку предприятий, характеризующую зависимость объема производства табачных изделий от влияния стоимости основных производственных фондов.
Рассчитаем число предприятий в % к итогу и полученные результаты поместим в итоговую группировочную таблицу.
| Группы по стоимости основных фондов, млн. р. | Число предприятий | Число предприятий в % к итогу | Объем производства изделий, тыс. шт. | |
| всего | в среднем | |||
| 1,1 - 6,9 | 14 | 46,7 | 100575 | 7183,9 |
| 6,9 - 12,7 | 9 | 30,0 | 75920 | 8435,6 |
| 12,7 - 18,5 | 4 | 13,3 | 37800 | 9450,0 |
| 18,5 - 30,2 | 3 | 10,0 | 35000 | 11666,7 |
| Итого | 30 | 100,0 | 249295 | 8309,8 |
Анализ полученной таблицы позволяет сделать следующие выводы: числа в последнем столбце таблицы, показывающий средний объем производства в каждой из групп, увеличиваются, следовательно, с увеличением стоимости основных средств объем производства изделий возрастает, что позволяет предположить, что между указанными показателями существует прямая корреляционная связь.
Задача 5
На основании группировки, построенной в пункте 2 задачи 2 рассчитайте:
а) относительные величины структуры (по двум любым показателям);
б) средний размер товарной продукции на одного работающего по каждой выделенной группе;
б) средний размер основных производственных фондов на одно предприятие по каждой выделенной группе;
2. Результаты расчетов изложите в той же сводной групповой таблице, где и результаты группировки, дополнив ее соответствующими графами.
Решение: Используя результаты, полученные в п. 2 задачи 2, рассчитаем по объему производства и товарной продукции относительные величины структуры.
Для этого значения по каждой группе разделим на итоговые значения, выразив результат в процентах.
Средний размер товарной продукции на одного работающего по каждой выделенной группе найдем, разделив стоимость товарной продукции на численность персонала.
Средний размер основных производственных фондов на одно предприятие по каждой выделенной группе найдем, разделив размер основных фондов на число предприятий.
Результаты расчетов представим в сводной групповой таблице
| Группы по стоимости основных фондов, млн. р. | Число предприятий | Объем производства изделий, тыс. шт. | Товарная продукция в оптовых ценах предприятий, млн. р. | Численность персонала, чел. | Товарная продукция на одного работающего, тыс. р. | Стоимость ОПФ на одно предприятие | ||||
| всего | в % к итогу | всего | в % к итогу | |||||||
| 1,1 - 6,9 | 14 | 100575 | 40,3 | 595,2 | 31,7 | 8966 | 66,384 | 4,043 | ||
| 6,9 - 12,7 | 9 | 75920 | 30,5 | 609,9 | 32,4 | 5266 | 115,818 | 9,244 | ||
| 12,7 - 18,5 | 4 | 37800 | 15,2 | 295,6 | 15,7 | 3319 | 89,063 | 15,550 | ||
| 18,5 - 30,2 | 3 | 35000 | 14,0 | 379 | 20,2 | 2915 | 130,017 | 27,133 | ||
| Итого | 30 | 249295 | 100,0 | 1879,7 | 100,0 | 20466 | 91,845 | 9,447 | ||
По результатам расчетов можно сделать следующие выводы: доминирующее положение по объему производства занимают предприятия, имеющие основные фонды в размере от 1,1 до 6,9 млн. р. Наибольший удельный вес товарной продукции в ее общей стоимости занимают предприятия, имеющие основные фонды в размере от 6,9 до 12,7 млн. р. и 1,1 до 6,9 млн. р. – 32,4% и 31,7% всей товарной продукции.
Индивидуальная работа 2
Задача 6
1. По исходным данным, представленным в таблице N1 (Вашего варианта) построить ряд распределения по численности промышленно-производственного персонала, образовав не более шести групп предприятий с равными интервалами. Результаты представьте в табличной форме.
2. По данным ряда распределения (см. пункт 1) построить гистограмму и полигон распределения и сформулируйте краткие выводы.
3. По полученному ряду распределения определите среднюю численность промышленно-производственного персонала, моду, медиану, квартили и коэффициент вариации.
Решение: Построим ряд распределения по численности промышленно-производственного персонала, образовав 5 групп предприятий с равными интервалами
Обозначим через х численность персонала. Определим размах варьирования признака х.
хmin = 291; хmax = 1535; R = хmax - хmin = 1535 – 291 = 1244.
Величина интервала равна h = R : m = 1244 : 5 = 249.
Выделим 5 групп с равными интервалами и подсчитаем количество вариантов в каждой из них.
1-я группа: [291; 540]
2- я группа: [540; 789]
3-я группа: [789; 1038]
4-я группа: [1038; 1287]
5-я группа: [1287; 1536]
Составим расчетную группировочную таблицу.
| Группа | Среднесписочная численность промышленно-производственного персонала, чел. |
| 291 – 540 | 291 |
| 304 | |
| 355 | |
| 366 | |
| 373 | |
| 377 | |
| 390 | |
| 426 | |
| 431 | |
| 432 | |
| 464 | |
| 475 | |
| 503 | |
| Количество в группе | 13 |
| 540 – 789 | 560 |
| 569 | |
| 604 | |
| 619 | |
| 679 | |
| 704 | |
| 740 | |
| 740 | |
| 744 | |
| 760 | |
| Количество в группе | 10 |
| 789 – 1038 | 946 |
| 964 | |
| Количество в группе | 2 |
| 1038 – 1287 | 1140 |
| 1142 | |
| Количество в группе | 2 |
| 1287 – 1536 | 1344 |
| 1489 | |
| 1535 | |
| Количество в группе | 3 |
| Общее количество | 30 |
Вычислим середины интервалов, сложив начало и конец интервала и разделив результат на 2. Вычислим относительные частоты, разделив частоту в интервале на общую сумму частот. Получим следующий интервальный ряд распределения.
| Интервал | 291 - 540 | 540 - 789 | 789 - 1038 | 1038 - 1287 | 1287 - 1536 | Сумма |
| Частота в интервале, 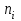 | 13 | 10 | 2 | 2 | 3 | 30 |
| Середина интервала | 415,5 | 664,5 | 913,5 | 1162,5 | 1411,5 | |
| Относительная частота | 0,43 | 0,33 | 0,07 | 0,07 | 0,10 | |
Построим полигон частот, отложив по горизонтальной оси значения
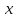 , а по вертикальной - соответствующие значения относительных частот.
, а по вертикальной - соответствующие значения относительных частот.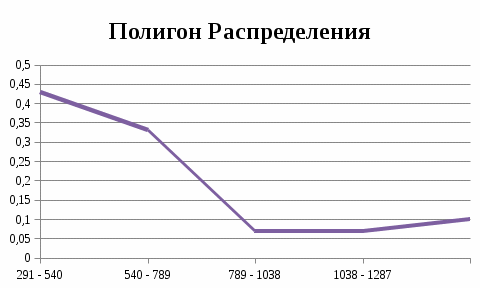
Построим гистограмму частот, отложив по горизонтальной оси интервалы изменения признака, а по вертикальной - соответствующие значения относительных частот.
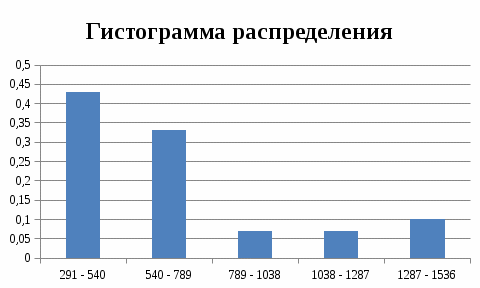
Найдем по полученному ряду распределения среднюю численность промышленно-производственного персонала, моду, медиану, квартили и коэффициент вариации. Среднюю найдем по формуле:
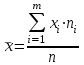 ,
, где n - объем выборки, m - количество интервалов, yi - середина i-го интервала.
Дисперсию найдем по формуле:
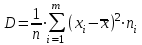
Составим вспомогательную таблицу
| Интервалы | Частоты, ni | Относительные частоты | Накопленные частоты | Середина интервала, xi | xini | (x – 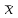 )2ni )2ni |
| 291 - 540 | 13 | 0,43 | 13 | 415,5 | 5401,5 | 917063,7 |
| 540 - 789 | 10 | 0,33 | 23 | 664,5 | 6645 | 2755,6 |
| 789 - 1038 | 2 | 0,07 | 25 | 913,5 | 1827 | 108019,5 |
| 1038 - 1287 | 2 | 0,07 | 27 | 1162,5 | 2325 | 463491,9 |
| 1287 - 1536 | 3 | 0,10 | 30 | 1411,5 | 4234,5 | 1600452 |
| | 30 | | | | 20433 | 3091783 |