Литература
1. ГОСТ 25346–89. Основные нормы взаимозаменяемости. Единая система допусков и посадок. Общие положения, ряды допусков и основных отклонений.– Режим доступа: http://gostexpert.ru/gost/gost-25346-82 (доступ свободный).

2. ГОСТ 25347–82. Основные нормы взаимозаменяемости. Единая система допусков и посадок. Поля допусков и рекомендуемые посадки.– Режим доступа: http://gostexpert.ru/gost/gost-25347-82 (доступ свободный).

3. Допуски и посадки[Текст]: Справочник. – В 2-х ч./ В. Д. Мягков, М. А. Палей, А. Б. Романов, В. А. Брагинский. – 6-е изд., перераб. и доп. – Л.: Машиностроение. Ленинградск. отд-ние, 1982. – Ч. 1. – 543 с.

4. Анурьев, В. И. Справочник конструктора-машиностроителя[Текст]: В 3 т. Т. 1. – 9-е изд., перераб. и доп. / В.И. Анурьев; под ред. И.Н. Жестковой. – М.: Машиностроение, 2006. – 928 с.

6. Марков, Н. Н., Осипов В. В., Шабалина М. Б. Нормирование точности в машиностроении[Текст]: Учеб.для машиностроит. спец. вузов / Н. Н. Марков, В. В. Осипов, М. Б. Шабалина; под ред. Ю. М. Соломенцова. – М.; Высш. шк.; Издательский центр «Академия», 2001. – 335 с.
Практическая работа №5
Расчет размерных цепей методом полной взаимозаменяемости
Цель работы
Закрепить теоретические знания по обеспечению точности размерных цепей.

Овладеть расчетом размерных цепей методом полной взаимозаменяемости.
Общие понятия, методы расчета и расчетные зависимости
В рабочей программе дисциплины отсутствует возможность в полной мере проработать в лекционные часы тематику размерных цепей, поэтому ниже представлены в достаточной мере развернутые материалы по основным понятиям и расчету размерных цепей.

Размерной цепью называется совокупность размеров, образующих замкнутый контур, определяющих взаимное положение поверхностей (или осей) одной или нескольких деталей и непосредственно участвующих в решении поставленной задачи.

Звеном называется каждый из размеров, образующих размерную цепь. Звеньями размерной цепи могут быть любые линейные или угловые параметры: диаметральные размеры, расстояния между поверхностями или осями, зазоры, натяги, перекрытия, мертвые ходы, отклонения формы и расположения поверхностей (осей) и т. д.

Любая размерная цепь имеет одно исходное (замыкающее) звено и два или более составляющих звеньев.

Исходным (А_Δ) называется звено, к которому предъявляется основное требование точности, определяющее качество изделия в соответствии с техническими условиями. Понятие исходного звена используется при проектном расчете размерной цепи. В процессе обработки или при сборке изделия исходное звено получается обычно последним, замыкая размерную цепь. В этом случае такое звено именуется замыкающим. Понятие замыкающего звена используется при поверочном расчете размерной цепи.

---

Составляющими (А₁, А₂ …) называются все остальные звенья, с изменением которых изменяется и замыкающее звено.

Составляющие звенья размерной цепи разделяются на две группы. К первой группе относятся звенья, с увеличением которых (при прочих постоянных) увеличивается и замыкающее звено. Такиезвенья называются увеличивающими.

Ко второй группе относятся звенья, с увеличением которых уменьшается замыкающее звено. Такие звенья называются уменьшающими.

Таким образом, если принять, что в размерной цепи общее количество звеньевm, то число составляющих звеньев составит m–1, из которых число увеличивающих обозначим n, а уменьшающих – k.

В сложных размерных цепях можно выявить увеличивающие и уменьшающие звенья, применив правило обхода по контуру. На схеме размерной цепи исходному звену предписывается определенное направление, обозначаемое стрелкой над буквенным обозначением.

Все составляющие звенья также обозначаются стрелками, начиная от звена, соседнего с исходным, и должны иметь один и тот же замкнутый поток направлений. Тогда все составляющие звенья, имеющие то же направление стрелок, что и у исходного звена, будут уменьшающими, а остальные звенья цепи — увеличивающими.

Сущность расчета размерной цепи заключается в установлении допусков и предельных отклонений всех ее звеньев исходя из требований конструкции и технологии.

При этом решают прямую и обратную задачи.

Прямая задача. По заданным номинальному размеру и допуску (отклонениям) исходного звена и номинальным размерам составляющих звеньев определить допуски и предельные отклонения составляющих звеньев размерной цепи. Такая задача относится к проектировочному расчету размерной цепи.

Обратная задача. По установленным номинальным размерам, допускам и предельным отклонениям составляющих звеньев определить номинальный размер, допуск и предельные отклонения замыкающего звена. Такая задача относится к проверочному расчету размерной цепи.

Решением обратной задачи проверяется правильность решения прямой задачи.

Существуют методы расчета размерных цепей, которые при внедрении результатов расчета обеспечивают полную и неполную (ограниченную) взаимозаменяемость. Методы расчета нормированы стандартом РД 50-635–87.

---

Расчет размерной цепи методом, обеспечивающим полную взаимозаменяемость,позволяет получить заданную точность размера исходного (замыкающего) звена, когда размеры составляющих звеньев могут иметь предельные допустимые значения, т. е. максимальные и минимальные. Поэтому метод называется также расчетом на максимум-минимум.

Для каждой размерной цепи при расчете на максимум-минимум действуют следующие виды уравнений:

– номинальных размеров


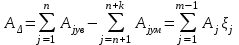(1)
; (1)

– предельных размеров


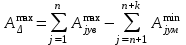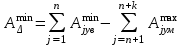(2)
;

; (2)

– предельных отклонений

;

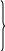
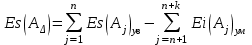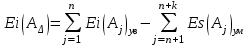; (3)

– допусков (точности)

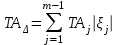; (4)

– координат середины полей допусков
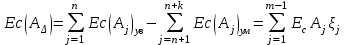; (5)
– предельных отклонений, на основе уравнения (5)
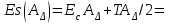
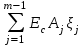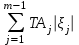+ /2;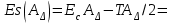

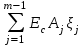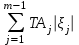– /2, (6)

где n – количество увеличивающих звеньев;

k – количество уменьшающих звеньев;

m – общее количество звеньев, включая замыкающее звено;

Es– верхнее отклонение звена;

Ei – нижнее отклонение звена,

ξ – передаточное отношение i – го составляющего звена, характеризующее влияние размера (и отклонений) составляющего звена на размер (и отклонения) исходного звена.

---

Координата середины поля допуска определяется, как
Е_сА_j= (EsA_j + EiA_j)/2. (7)
В случае параллельного расположения звеньев размерной цепи ξ =+1 для увеличивающих звеньев и ξ = –1 – для уменьшающих звеньев. Когда звенья размерной цепи расположены не параллельно, размер (и отклонения) составляющих звеньев берется в виде проекции на направление замыкающего звена.

Смешанное обозначение предельных отклонений из прописных и строчных букв объясняется тем, что звенья по конструктивному признаку могут быть отнесены как к охватывающим, так и к охватываемым размерам или быть промежуточным между ними, как, например, длина уступов на валах.

Существует несколько способов расчета допусков составляющих звеньев размерной цепи.

Для цепей с малым числом звеньев можно применить способ пробных расчетов, при использовании которого на основании конструкторско-технологического и производственного опыта подбирают допуски, выдерживая соотношение
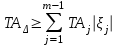. (8)

Способ равных допусков применяют, если составляющие размеры имеют один порядок (например, входят в один интервал размеров системы допусков и посадок) и могут быть выполнены с примерно одинаковой экономической точностью. В этом случае из формулы (4) получим средний допуск на звено
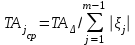. (9)

Этот допуск корректируют для составляющих размеров, так как в общем случае расчетный допуск может оказаться не целым числом, а также исходя из целесообразности учета различных конструктивных требований и технологических возможностей изготовления, но так, чтобы выполнялись условия по уравнениям (3) и (4). При этом выбирают стандартные поля допусков, желательно предпочтительного применения.

Способ равных допусков прост, но недостаточно точен, так как корректировка допусков составляющих размеров произвольна. Его можно рекомендовать только для предварительного назначения допусков составляющих размеров.

Способ допусков одного квалитета(одинаковых точностей) применяют, если все составляющие цепь размеры могут быть выполнены с допуском одного квалитета, при этом размеры составляющих звеньев находятся не в одном интервале размеров и соответственно должны иметь отличающиеся по величине допуски.

Требуемый квалитет определяют следующим образом.

---

Допуск составляющего размера
ТА_j = k_ji_j, (10)
где i – единица допуска (мкм);

k – число единиц допуска, содержащееся в допуске данного размера (определяется по ГОСТ 25346или таблице 1).

Для размеров от 1 до 500 ммi = 0,45 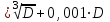, где D — средний геометрический размер (мм) для интервала размеров по ГОСТ 25346, к которому относится данный линейный размер.

Подставив выражение (10) в уравнение (4), определим расчетное значение числа единиц допуска k_с:
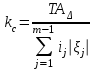. (11)
Если в размерной цепи имеются звенья с заранее известными допусками (например, ширин кольца подшипника качения), то в формуле (11) эти допуски вычитают из допуска исходного звена ТА_Δ, одновременно уменьшая знаменатель на величину, равную количеству таких звеньев.

По значению k_с выбирают ближайший квалитет. Число единиц допуска k_с, вычисленное по формуле (11), в общем случае не равно какому-либо стандартному значению k, определяющему квалитет, поэтому выбирают ближайший меньший квалитет. Найдя по ГОСТ 25346 или по ГОСТ 25347 (или таблице 2) допуски составляющих размеров, корректируют их значения для части звеньев в сторону большего квалитета, учитывая конструктивно-эксплуатационные требования и возможность применения процесса изготовления, экономическая точность которого близка к требуемой точности размеров.

В ряде случаев целесообразно выделить специальное звено, за счет расчета допуска которого выдержать требование зависимости (4). Величина допуска специального звена определяется формулой
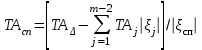. (12)
Полученная величина допуска ТА_сп уточняется подбором ближайшего предпочтительно меньшего стандартного значения по соответствующему квалитету.

Допуски для охватывающих размеров рекомендуется определять, как для основного отверстия, а для охватываемых — как для основного вала. Используется и другая рекомендация – предельные отклонения для увеличивающих звеньев принимать со знаком «+», уменьшающих – со знаком «–» и численно равные допуску. При этом следует удовлетворить уравнению (4).

---

Смотрите также файлы

• 1Понятие продуктивной деятельности и особенности организации занятий по аппликации во второй младшей группе. 5.docx

• Европы христианские философы и богословы Фома Аквинский 1225 1274 xiiiв.docx

• Задание Норма права.docx

• Лабораторная работа 11 Исследование трехфазного синхронного генератора Цель работы.docx

• Задание Норма права.docx