Файл: 1. Тип 20 26578 Из пункта a в пункт b одновременно выехали два автомобиля.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 148
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Решение. Пусть u км/ч — скорость первого теплохода, тогда скорость второго теплохода по течению равна
км/ч. Первый теплоход находился в пути на 1 час больше, чем второй, отсюда имеем:
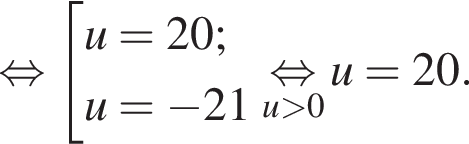
Таким образом, скорость первого теплохода равна 20 км/ч.
Ответ: 20.
7. Тип 20 № 26591
От пристани A к пристани B отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним со скоростью на 1 км/ч большей отправился второй. Расстояние между пристанями равно 110 км. Найдите скорость второго теплохода, если в пункт B он прибыл одновременно с первым. Ответ дайте в км/ч.
Решение. Пусть u км/ч — скорость второго теплохода, тогда скорость первого теплохода равна
км/ч. Первый теплоход находился в пути на 1 час больше, чем второй, отсюда имеем:
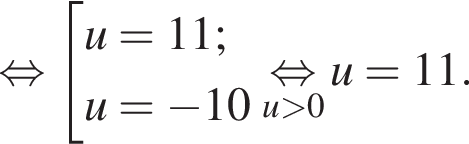
Ответ: 11.
8. Тип 20 № 26610
Баржа в 10:00 вышла из пункта A в пункт B, расположенный в 15 км от
Пробыв в пункте B 1 час 20 минут, баржа отправилась назад и вернулась в пункт A в 16:00 того же дня. Определите (в км/час) скорость течения реки, если известно, что собственная скорость баржи равна км/ч.Решение. Пусть u км/ч — скорость течения реки, тогда скорость баржи по течению равна
км/ч, а скорость баржи против течения равна 
км/ч. Баржа вернулась в пункт A через 6 часов, но пробыла в пункте B час 20 минут, поэтому общее время движения баржи дается уравнением:
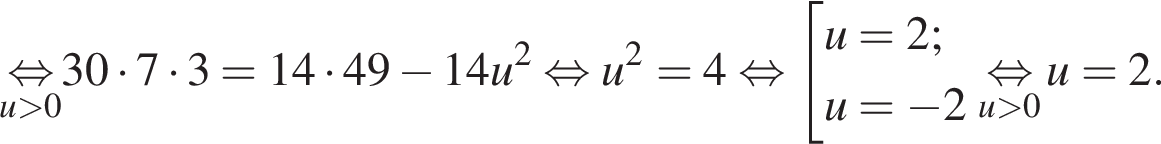
Поэтому скорость течения реки равна 2 км/ч.
Ответ: 2.
9. Тип 20 № 27482
Пристани A и B расположены на озере, расстояние между ними 390 км. Баржа отправилась с постоянной скоростью из A в
На следующий день после прибытия она отправилась обратно со скоростью на 3 км/ч больше прежней, сделав по пути остановку на 9 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в Найдите скорость баржи на пути из A в Ответ дайте в км/ч.Решение. Пусть u км/ч — скорость баржи на пути из A в B, тогда скорость баржи на пути из B в A
км/ч. На обратном пути баржа сделала остановку на 9 часов, и в результате она затратила на обратный путь столько же времени, сколько и на прямой, отсюда имеем:
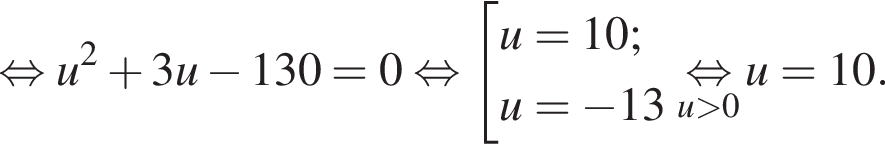
Поэтому собственная скорость баржи равна 10 км/ч.
Ответ: 10.
10. Тип 20 № 99601
Теплоход, скорость которого в неподвижной воде равна 25 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 30 часов после отплытия из него. Сколько километров прошел теплоход за весь рейс?
Решение. Пусть весь путь теплохода равен
км. Время в пути составляет 30 часов, из которых 5 часов — стоянка:
Тем самым, весь пути теплохода составляет 2 · 308 = 616 км.
Ответ: 616.
11. Тип 20 № 99602
Расстояние между пристанями A и B равно 120 км. Из A в B по течению реки отправился плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в
К этому времени плот прошел 24 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.Решение. Скорость плота равна скорости течения реки 2 км/ч. Пусть u км/ч — скорость яхты, тогда скорость яхты по течению равна
км/ч, а скорость яхты против течения равна 
км/ч. Яхта, прибыв в пункт B, тотчас повернула обратно и возвратилась в A, а плоту понадобилось на час больше времени, чтобы пройти 24 км.
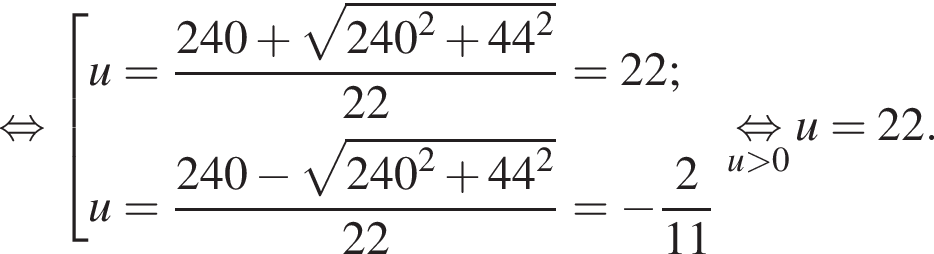
Ответ: 22.
12. Тип 20 № 99604
Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
Решение. Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Пусть
км — весь путь путешественника, тогда средняя скорость равна:
Поэтому средняя скорость путешественника 38,4 км/ч.
Ответ: 38,4.
13. Тип 20 № 99610
По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Решение. Пока сухогрузы перейдут из первого положения во второе, второй сухогруз переместился относительно первого на
м.Пусть u − разность скоростей сухогрузов, тогда
м/мин
км/ч.Ответ: 6.
ЗАДАЧИ ДВИЖЕНИЕ ПО КРУГУ
1. Тип 20 № 99596
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Решение. Пусть υ км/ч — скорость первого мотоциклиста, тогда скорость второго мотоциклиста равна υ + 21 км/ч. Пусть первый раз мотоциклисты поравняются через t часов. Для того, чтобы мотоциклисты поравнялись, более быстрый должен преодолеть изначально разделяющее их расстояние, равное половине длины трассы. Поэтому
Таким образом, мотоциклисты поравняются через
часа или через 20 минут.Ответ: 20.
Приведём другое решение.
Быстрый мотоциклист движется относительно медленного со скоростью 21 км в час, и должен преодолеть разделяющие их 7 км. Следовательно, на это ему потребуется одна треть часа.
2. Тип 20 № 99598
Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.