Файл: 1. Тип 20 26578 Из пункта a в пункт b одновременно выехали два автомобиля.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 149
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Ответ дайте в км/ч.
Решение. Пусть км/ч — скорость первого автомобиля. Автомобиль, выехавший из города B, преодолел расстояние (470 − 350) км = 120 км. Первый автомобиль находился в пути на 3 часа больше, чем второй. Таким образом,
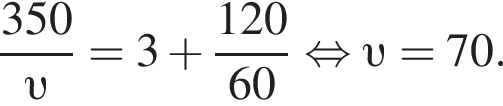
Ответ: 70.
12. Тип 20 № 99592
Из городов A и B навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 3 часа раньше, чем велосипедист приехал в A, а встретились они через 48 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
Решение. Примем расстояние между городами 1. Пусть время движения велосипедиста равно x ч, тогда время движения мотоциклиста равно ч,
ч,  К моменту встречи они находились в пути 48 минут и в сумме преодолели всё расстояние между городами, поэтому
К моменту встречи они находились в пути 48 минут и в сумме преодолели всё расстояние между городами, поэтому
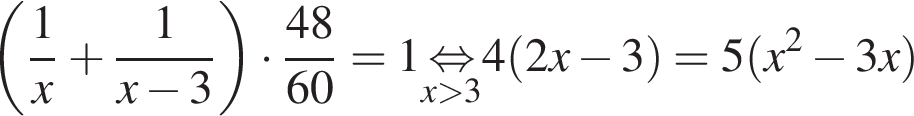
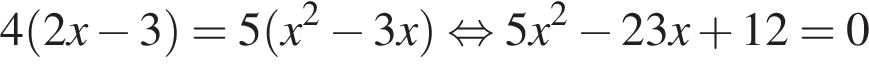
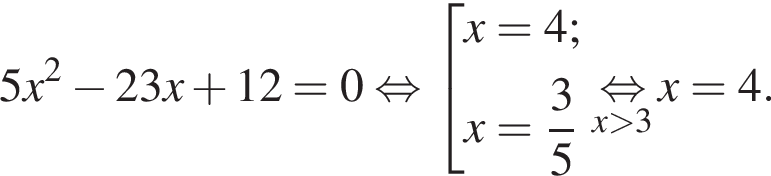
Таким образом, велосипедист находился в пути 4 часа.
Ответ: 4.
13. Тип 20 № 99593
Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Решение. Скорость товарного поезда меньше, чем скорого на 750 м/мин или на
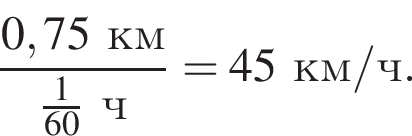
Пусть υ км/ч — скорость товарного поезда, тогда скорость скорого поезда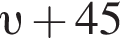
км/ч. На путь в 180 км товарный поезд тратит времени на 2 часа больше, чем скорый, отсюда имеем:
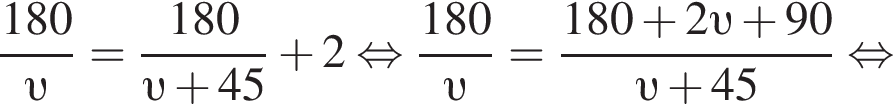
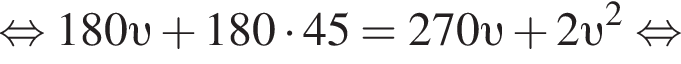
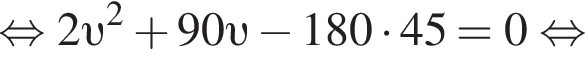
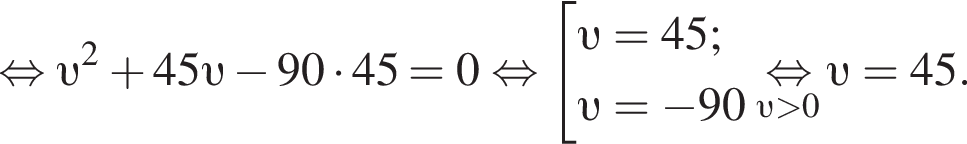
Ответ: 45.
14. Тип 20 № 99594
Расстояние между городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в Найдите расстояние от A до
Найдите расстояние от A до 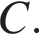 Ответ дайте в километрах.
Ответ дайте в километрах.
Решение. Обозначим S км — расстояние от A до C, υ км/ч — скорость автомобиля, t ч — время движения мотоциклиста от A до C. Тогда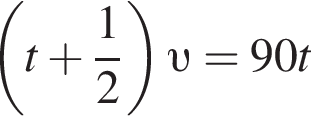 и
и 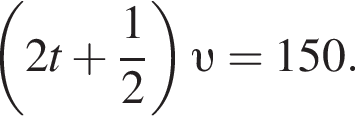 Решим систему полученных уравнений:
Решим систему полученных уравнений:
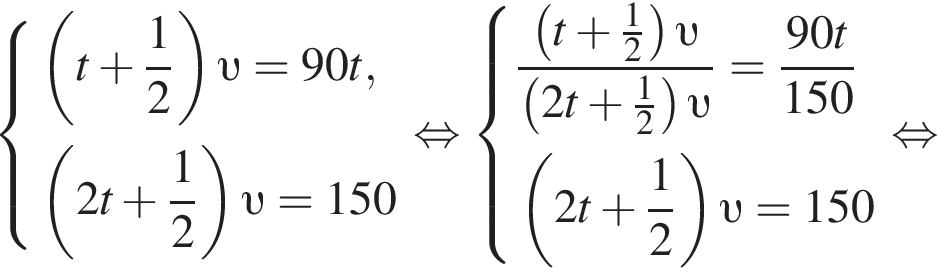
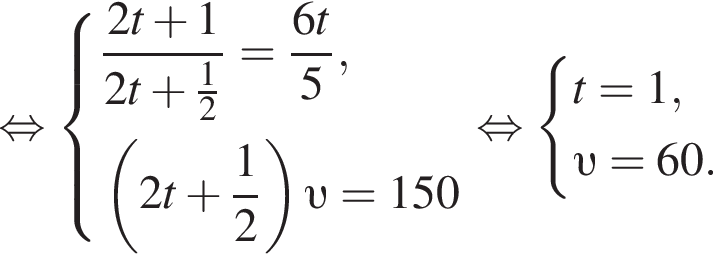
Тогда км.
км.
Ответ: 90.
15. Тип 20 № 99595
Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?
Решение. Пусть км/ч — скорость второго пешехода, тогда скорость первого −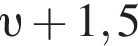 км/ч. Пусть через t часов расстояние между пешеходами станет равным 0,3 километра. Таким образом,
км/ч. Пусть через t часов расстояние между пешеходами станет равным 0,3 километра. Таким образом,

 часа или
часа или  минут.
минут.
Ответ: 12.
16. Тип 20 № 99597
Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
Решение. Пусть км/ч — скорость третьего велосипедиста, а t ч — время, которое понадобилось ему, чтобы догнать второго велосипедиста. Таким образом,
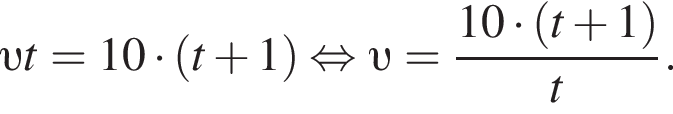
А через 2 часа 20 минут после этого третий велосипедист догнал первого. Таким образом,
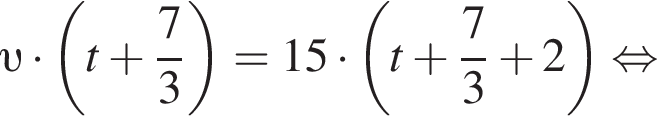
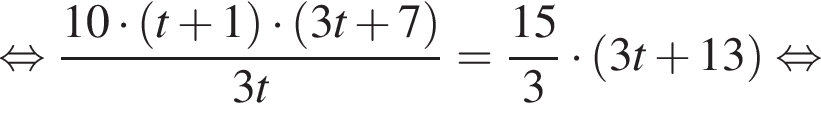
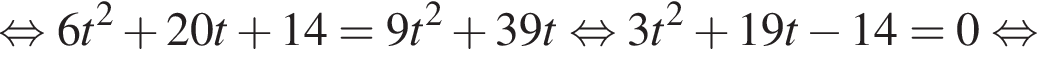
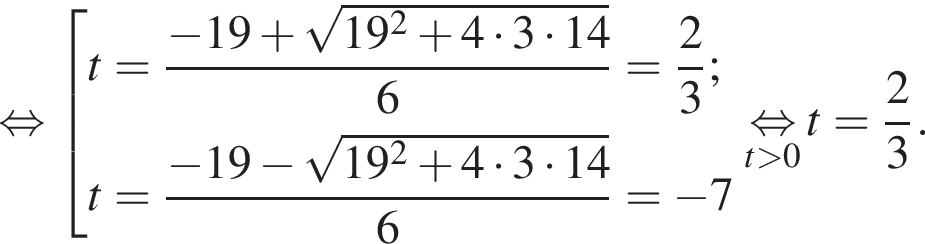
Таким образом,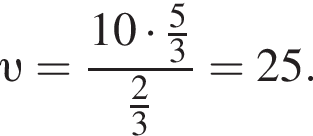
Ответ: 25.
Приведем другое решение.
Примем за х км/ч скорость третьего велосипедиста. Тогда скорость сближения второго и третьего велосипедистов равна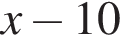 км/ч, а скорость сближения первого и третьего велосипедистов равна
км/ч, а скорость сближения первого и третьего велосипедистов равна 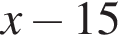 км/ч. Второй велосипедист выехал на час раньше третьего, поэтому изначально их разделяло 10 км. Чтобы преодолеть это расстояние, третьему велосипедисту понадобилось
км/ч. Второй велосипедист выехал на час раньше третьего, поэтому изначально их разделяло 10 км. Чтобы преодолеть это расстояние, третьему велосипедисту понадобилось 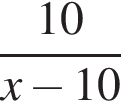 часа. Первый велосипедист выехал на два часа раньше третьего, поэтому изначально их разделяло 30 км. Следовательно, третий велосипедист догнал первого за
часа. Первый велосипедист выехал на два часа раньше третьего, поэтому изначально их разделяло 30 км. Следовательно, третий велосипедист догнал первого за 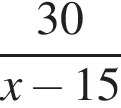 часа. Третий велосипедист догнал первого через 7/3 часа после того, как он догнал второго, поэтому можно составить уравнение:
часа. Третий велосипедист догнал первого через 7/3 часа после того, как он догнал второго, поэтому можно составить уравнение:
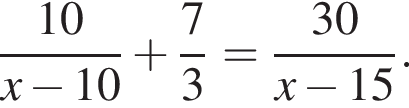
При условии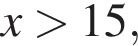 избавляясь от знаменателей, получаем:
избавляясь от знаменателей, получаем:
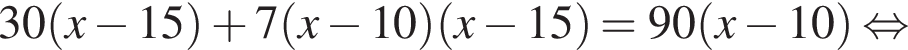
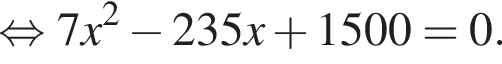
Найдем дискриминант:
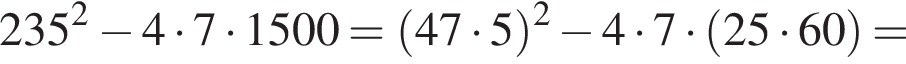
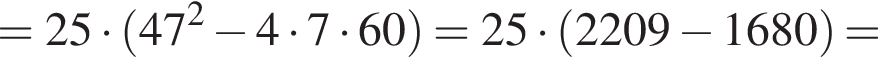
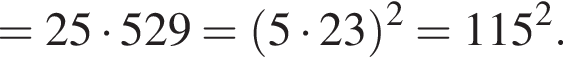
Следовательно,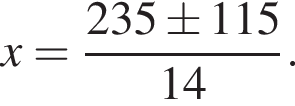
Меньший корень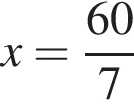 меньше 15, а потому не подходит. Больший корень, равный 25, подходит. Скорость третьего велосипедиста равна 25 км/ч.
меньше 15, а потому не подходит. Больший корень, равный 25, подходит. Скорость третьего велосипедиста равна 25 км/ч.
17. Тип 20 №
99603
Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени — со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение. Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Пусть автомобиль находился в пути часов, тогда его средняя скорость равна:
часов, тогда его средняя скорость равна:
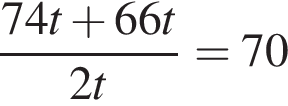 км/ч.
км/ч.
Ответ: 70.
18. Тип 20 № 99605
Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть — со скоростью 120 км/ч, а последнюю — со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение. Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Пусть км — весь путь автомобиля, тогда средняя скорость равна:
км — весь путь автомобиля, тогда средняя скорость равна:
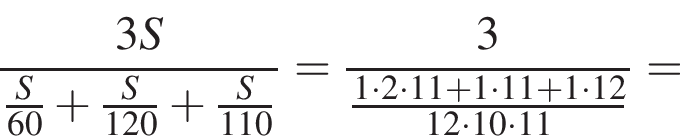
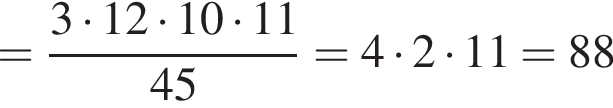 км/ч.
км/ч.
Ответ: 88.
19. Тип 20 № 99606
Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час — со скоростью 100 км/ч, а затем два часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение. Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Средняя скорость равна:
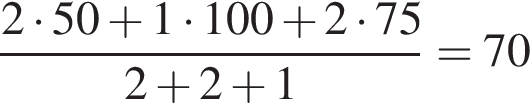
Решение. Пусть км/ч — скорость первого автомобиля. Автомобиль, выехавший из города B, преодолел расстояние (470 − 350) км = 120 км. Первый автомобиль находился в пути на 3 часа больше, чем второй. Таким образом,
Ответ: 70.
12. Тип 20 № 99592
Из городов A и B навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 3 часа раньше, чем велосипедист приехал в A, а встретились они через 48 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
Решение. Примем расстояние между городами 1. Пусть время движения велосипедиста равно x ч, тогда время движения мотоциклиста равно
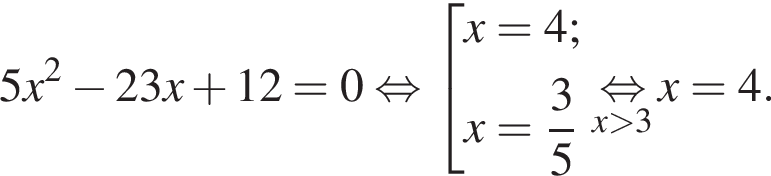
Таким образом, велосипедист находился в пути 4 часа.
Ответ: 4.
13. Тип 20 № 99593
Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Решение. Скорость товарного поезда меньше, чем скорого на 750 м/мин или на
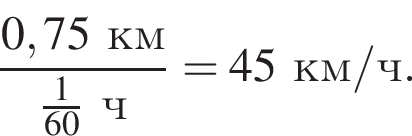
Пусть υ км/ч — скорость товарного поезда, тогда скорость скорого поезда
км/ч. На путь в 180 км товарный поезд тратит времени на 2 часа больше, чем скорый, отсюда имеем:
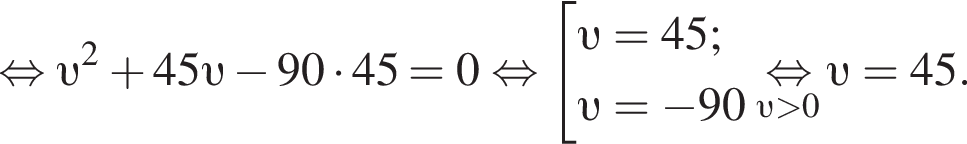
Ответ: 45.
14. Тип 20 № 99594
Расстояние между городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в
Решение. Обозначим S км — расстояние от A до C, υ км/ч — скорость автомобиля, t ч — время движения мотоциклиста от A до C. Тогда
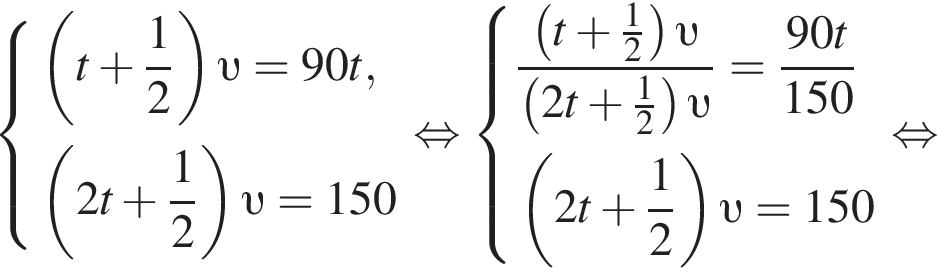
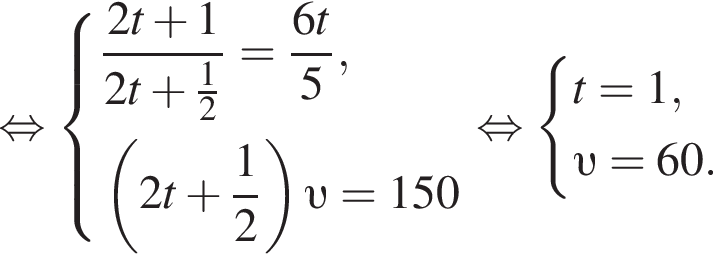
Тогда
Ответ: 90.
15. Тип 20 № 99595
Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?
Решение. Пусть км/ч — скорость второго пешехода, тогда скорость первого −
Ответ: 12.
16. Тип 20 № 99597
Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
Решение. Пусть км/ч — скорость третьего велосипедиста, а t ч — время, которое понадобилось ему, чтобы догнать второго велосипедиста. Таким образом,
А через 2 часа 20 минут после этого третий велосипедист догнал первого. Таким образом,
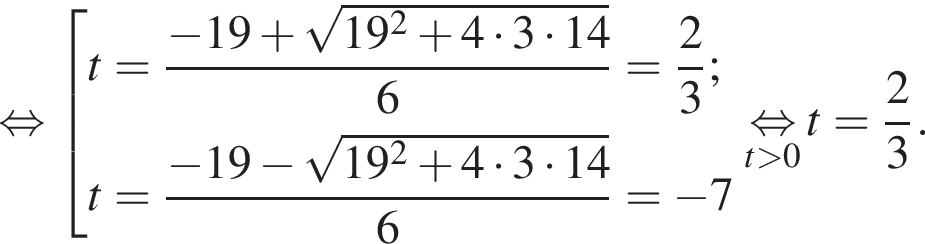
Таким образом,
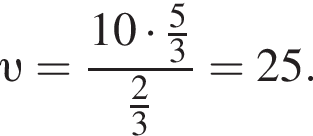
Ответ: 25.
Приведем другое решение.
Примем за х км/ч скорость третьего велосипедиста. Тогда скорость сближения второго и третьего велосипедистов равна
При условии
Найдем дискриминант:
Следовательно,
Меньший корень
17. Тип 20 №
99603
Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени — со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение. Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Пусть автомобиль находился в пути
Ответ: 70.
18. Тип 20 № 99605
Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть — со скоростью 120 км/ч, а последнюю — со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение. Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Пусть
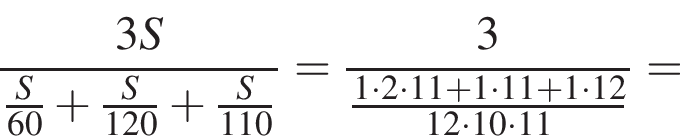
Ответ: 88.
19. Тип 20 № 99606
Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час — со скоростью 100 км/ч, а затем два часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение. Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Средняя скорость равна: