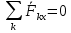Файл: 18 Условие жёсткой связи неизменяемые мехе сисмы Конфигурация матго тела Теорема Грасгофа о проекциях скоростей.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 82
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
=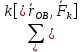 +
+ =
=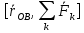 +
+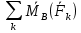 =[
=[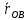 ,
,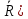 +
+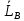 .
.
Формула со (*) называется фор Пуансо
Следствие:если главный вектор системы сил=0 то ее главный момент не меняется при смене полюса (т.е представляет собой свободный вектор).
5) Аксиомы статики: аксиома о связях. Реакции связей.
Связь-напередзаданное ограничение на движение тела.Реакции связей –силы действующие на тела со стороны связей.Связь-двусторонняя если все возможные перемещения не освобождающие(если беск малое перемещение явл возможным)
Ньютоновы силы:реакции связей,активные силы. Активные силы –ньют. С силы не являющиеся реакциями связей.
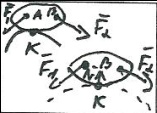
Аксиома освобождаемости от связи.
Состояние тела(или системы тел) не изменится если отбросить какие-либо из наложенных связей ,заменив действия связей их реакцией. Пример(точечный контакт гладких пов-ей). Из аксиомы следует что любое несвободное тело можно рассматривать как свободное добавив к активным силам реакции связи.
Аксиома о наложении новых связей.
Состояние покоя механической системы(или мат-ого тела) не нарушится если наложить новые связи.Частный случай(принцип отвердевания)-состояние покоя мат-ого тела не наруш если путем наложения новых связей превр. его в атт.
6) Теорема о приведении произвольной системы сил к двум силам.
Любую систему сил при помощи элементарных операций можно привести к 2 силам одна из которых приложена в напередзаданной точке.
1)Если заданная точка О не явл точкой приложения ни одной из сил системы Добавим к системе силу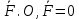 Имеем систему {
Имеем систему {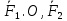 .
.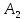 ,…,
,…,
}
2)Если n=2,то теорема доказана. Если n=1 достаточно добавить где-либо нулевую систему. Далее считаем что n=>3
3)Введем обозначения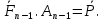 A,
A,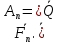 .B. Проведем плоскости через:
.B. Проведем плоскости через: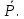 и O,
и O,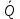 B O. На линии L пересечения плоскостей возьмем точку С отличную от 0
B O. На линии L пересечения плоскостей возьмем точку С отличную от 0
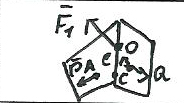
4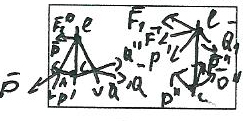 )Проведем прямые АО,ВО,АС,ВС и разложим :
)Проведем прямые АО,ВО,АС,ВС и разложим :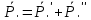 ,
,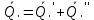
5)Перенесем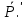 и
и 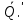 вдоль линии действия в О и сложим с
вдоль линии действия в О и сложим с  :
: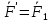 +
+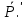 +
+ 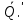 Перенесем
Перенесем 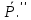 и
и 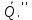 в С:
в С: 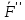 =
=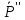 +
+ 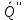
6)Исходная система заменена эквивалентной системой из n-1 силы: {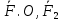 .
. ,…,
,…,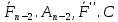 }
}
Если n=3 то теорема доказана.Если n>3 замена n на n-1 к 3)
В итоге получаем:{ ,…,
,…,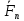 }эквивалентно{
}эквивалентно{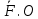 ,
,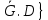 Теорема прин Эйлеру
Теорема прин Эйлеру
7) Пара сил, её плечо и момент. Теорема о приведении произвольной сис-мы сил к силе и паре.
Пара сил-система 2 сил = по модулю и противоположнонаправленных. Для пары сил главный вектор=0 а гл момент не зависит от выбора полюса
Момент пары сил -свободный вектор = векторному произведению радиус-вектора точки приложения одной из сил пары проведенного из др точки приложения на эту силу.
Плечо пары сил- расстояние между линиями действия сил пары.
Следствие 1
Если момент = 0 то силы пары лежат на одной прямой и такая пара по аксиоме о 2 силах экв 0 явл элементарной нуль-системой.
Следствие 2
Если момент не = 0 то пара сил:1)не экв 0 2)не приводится к равнодействующей. Момент пары ортог пл-ти пары и направлен в ту сторону откуда поворот который стремится вызвать пара виден происходящему против хода часовой стрелки.
Теорема о приведении системы сил к силе и паре. Любую систему сил при помощи элементарных операций можно привести к силе приложенной в напередзад точке О-центре приведения и паре сил.
1)По теореме о привед к 2 силам { ,…,
,…, }эквивалентно{
}эквивалентно{ ,
, ;гл вектор и гл момент сохр при помощи злеем-ых преобразований.
;гл вектор и гл момент сохр при помощи злеем-ых преобразований.
2)Добавим нуль-систему {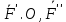 .O }
.O } 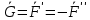 ,а затем сложим
,а затем сложим  и
и 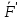 :
: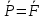 +
+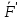 Получим {
Получим { ,
,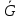 }экв{
}экв{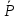 ,
,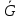 ,
, } Cила
} Cила 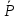 и {
и {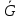
, }-искомые. При этом
}-искомые. При этом  =
= +
+ +
+ =
= тогда
тогда 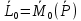 +
+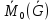 +
+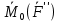 =
= (
( ,
, )
)
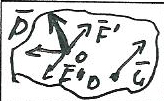
Замечание: можно показать что справедлив след-ий критерий экв-ти систем сил: любые 2 системы сил экв-ныу них = гл векторы и гл моменты. Вывод: пара сил полностью(с точн до экв-ти) харак-ся своим моментом.
8) Теорема об условиях равновесия АТТ. Ур-я равновесия для пространственной сис-мы сил
Теорема равновесия АТТ
Для того чтобы произвольная система сил была уравнов-ой необходимо и достаточно чтобы ее главный вектор и гл момент относ-но произв-ого полюса В=0 (*) =0, .
=0, . 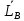 =0
=0
1)Необходимость. Имеем: { ,…,
,…, }экв0 По теореме о приведении к 2 силам {
}экв0 По теореме о приведении к 2 силам { ,…,
,…, }экв{
}экв{ .
.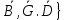 По аксиоме о 2 силах {
По аксиоме о 2 силах { ,
, }экв0
}экв0 =-
=-
и //
//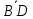 Первое рав-во означ что
Первое рав-во означ что 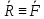 +
+ =0 а силы
=0 а силы  и
и  образуют пару поскольку она экв нулю.
образуют пару поскольку она экв нулю. 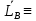 M(
M( ,
, )=0
)=0
2)Достаточность. Исходим из равенства (*).По теореме о приведении к силе и паре: { ,…,
,…, }экв{
}экв{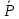 .
.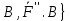 где {
где { ,
, } –пара сил,т.е
} –пара сил,т.е 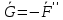 ,но
,но 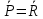 =0,итак {
=0,итак { ,…,
,…, }экв{
}экв{ ,
, },для этой пары сил
},для этой пары сил  (
( ,
, )=
)=  =0,поэтому {
=0,поэтому { ,
, }экв0,т.е {
}экв0,т.е { ,…,
,…, }экв0.
}экв0.
≤простой системы сил. Пусть xyz-произвольная декартовая система координат. Следствие:уравнения равновесия произв системы сил в скалярной форме:
X: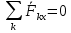
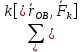 +
+ =
=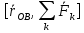 +
+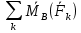 =[
=[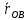 ,
,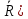 +
+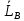 .
.Формула со (*) называется фор Пуансо
Следствие:если главный вектор системы сил=0 то ее главный момент не меняется при смене полюса (т.е представляет собой свободный вектор).
5) Аксиомы статики: аксиома о связях. Реакции связей.
Связь-напередзаданное ограничение на движение тела.Реакции связей –силы действующие на тела со стороны связей.Связь-двусторонняя если все возможные перемещения не освобождающие(если беск малое перемещение явл возможным)
Ньютоновы силы:реакции связей,активные силы. Активные силы –ньют. С силы не являющиеся реакциями связей.
Аксиома освобождаемости от связи.
Состояние тела(или системы тел) не изменится если отбросить какие-либо из наложенных связей ,заменив действия связей их реакцией. Пример(точечный контакт гладких пов-ей). Из аксиомы следует что любое несвободное тело можно рассматривать как свободное добавив к активным силам реакции связи.
Аксиома о наложении новых связей.
Состояние покоя механической системы(или мат-ого тела) не нарушится если наложить новые связи.Частный случай(принцип отвердевания)-состояние покоя мат-ого тела не наруш если путем наложения новых связей превр. его в атт.
6) Теорема о приведении произвольной системы сил к двум силам.
Любую систему сил при помощи элементарных операций можно привести к 2 силам одна из которых приложена в напередзаданной точке.
1)Если заданная точка О не явл точкой приложения ни одной из сил системы Добавим к системе силу
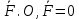 Имеем систему {
Имеем систему {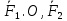 .
.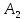 ,…,
,…,
}
2)Если n=2,то теорема доказана. Если n=1 достаточно добавить где-либо нулевую систему. Далее считаем что n=>3
3)Введем обозначения
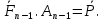 A,
A,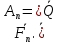 .B. Проведем плоскости через:
.B. Проведем плоскости через: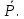 и O,
и O,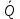 B O. На линии L пересечения плоскостей возьмем точку С отличную от 0
B O. На линии L пересечения плоскостей возьмем точку С отличную от 04
 )Проведем прямые АО,ВО,АС,ВС и разложим :
)Проведем прямые АО,ВО,АС,ВС и разложим :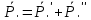 ,
,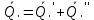
5)Перенесем
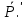 и
и 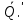 вдоль линии действия в О и сложим с
вдоль линии действия в О и сложим с  :
: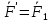 +
+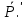 +
+ 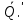 Перенесем
Перенесем 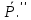 и
и 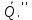 в С:
в С: 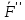 =
=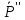 +
+ 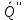
6)Исходная система заменена эквивалентной системой из n-1 силы: {
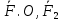 .
. ,…,
,…,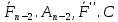 }
}Если n=3 то теорема доказана.Если n>3 замена n на n-1 к 3)
В итоге получаем:{
 ,…,
,…,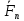 }эквивалентно{
}эквивалентно{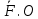 ,
,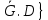 Теорема прин Эйлеру
Теорема прин Эйлеру
7) Пара сил, её плечо и момент. Теорема о приведении произвольной сис-мы сил к силе и паре.
Пара сил-система 2 сил = по модулю и противоположнонаправленных. Для пары сил главный вектор=0 а гл момент не зависит от выбора полюса
Момент пары сил -свободный вектор = векторному произведению радиус-вектора точки приложения одной из сил пары проведенного из др точки приложения на эту силу.
Плечо пары сил- расстояние между линиями действия сил пары.
Следствие 1
Если момент = 0 то силы пары лежат на одной прямой и такая пара по аксиоме о 2 силах экв 0 явл элементарной нуль-системой.
Следствие 2
Если момент не = 0 то пара сил:1)не экв 0 2)не приводится к равнодействующей. Момент пары ортог пл-ти пары и направлен в ту сторону откуда поворот который стремится вызвать пара виден происходящему против хода часовой стрелки.
Теорема о приведении системы сил к силе и паре. Любую систему сил при помощи элементарных операций можно привести к силе приложенной в напередзад точке О-центре приведения и паре сил.
1)По теореме о привед к 2 силам {
 ,…,
,…, }эквивалентно{
}эквивалентно{ ,
, ;гл вектор и гл момент сохр при помощи злеем-ых преобразований.
;гл вектор и гл момент сохр при помощи злеем-ых преобразований.2)Добавим нуль-систему {
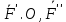 .O }
.O } 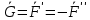 ,а затем сложим
,а затем сложим  и
и 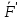 :
: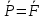 +
+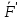 Получим {
Получим { ,
,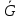 }экв{
}экв{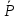 ,
,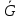 ,
, } Cила
} Cила 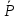 и {
и {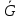
,
 }-искомые. При этом
}-искомые. При этом  =
= +
+ +
+ =
= тогда
тогда 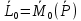 +
+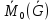 +
+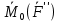 =
= (
( ,
, )
) Замечание: можно показать что справедлив след-ий критерий экв-ти систем сил: любые 2 системы сил экв-ныу них = гл векторы и гл моменты. Вывод: пара сил полностью(с точн до экв-ти) харак-ся своим моментом.
8) Теорема об условиях равновесия АТТ. Ур-я равновесия для пространственной сис-мы сил
Теорема равновесия АТТ
Для того чтобы произвольная система сил была уравнов-ой необходимо и достаточно чтобы ее главный вектор и гл момент относ-но произв-ого полюса В=0 (*)
 =0, .
=0, . 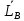 =0
=01)Необходимость. Имеем: {
 ,…,
,…, }экв0 По теореме о приведении к 2 силам {
}экв0 По теореме о приведении к 2 силам { ,…,
,…, }экв{
}экв{ .
.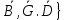 По аксиоме о 2 силах {
По аксиоме о 2 силах { ,
, }экв0
}экв0 =-
=-
и
 //
//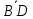 Первое рав-во означ что
Первое рав-во означ что 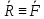 +
+ =0 а силы
=0 а силы  и
и  образуют пару поскольку она экв нулю.
образуют пару поскольку она экв нулю. 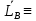 M(
M( ,
, )=0
)=02)Достаточность. Исходим из равенства (*).По теореме о приведении к силе и паре: {
 ,…,
,…, }экв{
}экв{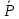 .
.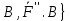 где {
где { ,
, } –пара сил,т.е
} –пара сил,т.е 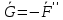 ,но
,но 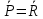 =0,итак {
=0,итак { ,…,
,…, }экв{
}экв{ ,
, },для этой пары сил
},для этой пары сил  (
( ,
, )=
)=  =0,поэтому {
=0,поэтому { ,
, }экв0,т.е {
}экв0,т.е { ,…,
,…, }экв0.
}экв0.≤простой системы сил. Пусть xyz-произвольная декартовая система координат. Следствие:уравнения равновесия произв системы сил в скалярной форме:
X: