Файл: Курсовая работа особенности изучения систем счисления в школьном курсе информатики.docx
Добавлен: 06.11.2023
Просмотров: 527
Скачиваний: 19
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Теоретические основы изучения систем счисления в школьном курсе информатики
Анализ темы: «Системы счисления» в школьном курсе информатики
Методические аспекты изучения системы счисления в школьном курсе информатики
2.1 Разработка контрольно-измерительных материалов по теме «Системы счисления»
2.2 Методические рекомендации изучения систем счисления в школьном курсе информатики
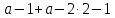
Целая часть будет равна
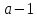
На втором шаге оставшуюся дробную часть опять умножим на 2, получим целую часть, равную
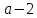
Описанный процесс необходимо продолжать до тех пор, пока в результате умножения мы не получим нулевую дробную часть или не будет достигнута требуемая точность вычислений.
Легко заметить, что последовательность полученных чисел совпадает с последовательностью цифр дробного двоичного числа, записанного в свернутой форме:
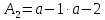
Алгоритм перевода правильной десятичной дроби в двоичную будет следующим:
-
Последовательно выполнять умножение исходной десятичной дроби и получаемых дробных частей произведений на основание системы (на 2) до тех пор, пока не получится нулевая дробная часть или не будет достигнута требуемая точность вычислений. -
Записать полученные целые части произведения в прямой последовательности.
В качестве примера рассмотрим перевод десятичной дроби 0,75 в двоичную систему, записывая результаты в таблицу:
В результате получаем двоичную дробь:
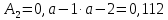
Перевод чисел из позиционной системы с произвольным основанием р в систему с основанием q производится по алгоритмам, аналогичным рассмотренным выше.
Далее рассмотрим алгоритм перевода целых чисел на примере перевода целого десятичного числа
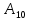= 42410 в шестнадцатеричную систему, то есть из системы счисления с основанием р = 10 в систему счисления с основанием q = 16.В процессе выполнения алгоритма необходимо обратить внимание, что все действия необходимо осуществлять в исходной системе счисления (в данном случае десятичной), а полученные остатки записывать цифрами новой системы счисления (в данном случае шестнадцатеричной).
Рассмотрим теперь алгоритм перевода дробных чисел на примере перевода десятичной дроби
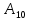
= 0,625 в восьмеричную систему, то есть из системы счисления с основанием р = 10 в систему счисления с основанием q = 8.
В процессе выполнения алгоритма необходимо обратить внимание, что все действия необходимо осуществлять в исходной системе счисления (в данном случае десятичной), а полученные остатки записывать цифрами новой системы счисления (в данном случае восьмеричной).
Перевод чисел из двоичной системы счисления в восьмеричную. Для записи двоичных чисел используются две цифры, то есть в каждом разряде числа возможны 2 варианта записи. Решаем показательное уравнение:
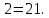Так как 
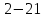, то I = 1 бит.Каждый разряд двоичного числа содержит 1 бит информации вариантов записи. Решим показательное уравнение
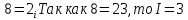бита. Каждый вариант восьмеричного числа содержит 3 бита информацииТаким образом, для перевода целого двоичного числа в восьмеричное его нужно разбить на группы по три цифры, справа налево, а затем преобразовать каждую группу в восьмеричную цифру. Если в последней, левой, группе окажется меньше трех цифр, то необходимо ее дополнить слева нулями.
Переведем таким способом двоичное число 1010012 в восьмеричное: 518
Для упрощения перевода можно заранее подготовить таблицу преобразования двоичных триад (групп по 3 цифры) в восьмеричные цифры:
окажется меньше четырех цифр, то необходимо дополнить ее справа нулями.
Затем надо преобразовать каждую группу в шестнадцатеричную цифру, воспользовавшись для этого предварительно составленной таблицей соответствия двоичных тетрад и шестнадцатеричных цифр.
Переведем целое двоичное число
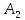= 1010012 в шестнадцатеричное:Для перевода дробного двоичного числа (правильной дроби) в восьмеричное необходимо разбить его на триады слева направо и, если в последней, правой, группе окажется меньше трех цифр, дополнить ее справа нулями. Далее необходимо триады заменить на восьмеричные числа.
Например, преобразуем дробное двоичное число
= 0,1101012 в восьмеричную систему счисления:Получаем:
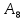= 0,658.Далее рассмотрим перевод числа из двоичной системы счисления в шестнадцатеричную.
Для записи шестнадцатеричных чисел используются шестнадцать цифр, то есть в каждом разряде числа возможны 16 вариантов записи. Решаем показательное уравнение:
16 = 21. Так как 16 = 24, то I = 4 бита.
Каждый разряд шестнадцатеричного числа содержит 4 бита информации.
Таким образом, для перевода целого двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры (тетрады), начиная справа, и, если в последней левой группе окажется меньше четырех цифр, дополнить ее слева нулями. Для перевода дробного двоичного числа (правильной дроби) в шестнадцатеричное необходимо разбить его на тетрады слева направо и, если в последней правой группе окажется меньше 4 цифр, то необходимо дополнить её справа нулями.
Для того чтобы преобразовать любое двоичное число в восьмеричную или шестнадцатеричную системы счисления, необходимо произвести преобразования по рассмотренным выше алгоритмам отдельно для его целой и дробной частей.
Для перевода чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную необходимо цифры числа преобразовать в группы двоичных цифр. Для перевода из восьмеричной системы в двоичную каждую цифру числа надо преобразовать в группу из трех двоичных цифр (триаду), а при преобразовании шестнадцатеричного числа – в группу из четырех цифр (тетраду).
- 1 2 3 4 5
Анализ темы: «Системы счисления» в школьном курсе информатики
Для анализа взяты учебники следующих авторов: Л. Л. Босова 10 класс и Н. Д Угринович 10 класс (профильный уровень)
У Л. Л. Босовой тема «Системы счисления» в учебнике находится в главе 3, с параграфов 10-12. Рассказывается о двоичной, восьмеричной и шестнадцатеричной систем счисления, а также о переводе из одной системы счисления в другую. А также о позиционных и непозиционных системах счисления.
Учебник Н. Д Угриновича направлен на профильный уровень изучения информатики. В базовом уровне информатике его учебника эта тема не рассматривается. По его программе тему «системы счисления» рассматривают в 10 классе. Изучение начинается с главы 2, параграфа 2.7 и до 2.9. там рассказывается про позиционные и непозиционные системы счисления, перевод из одной системы счисления в другу, а также арифметические операции в позиционных СС.
Л.Л Босова 5 часов на изучение систем счисления. Это обусловлено тем, что в курсе изучаются только переводы из одной системы счисления в другую. Отсутствует тема, посвящённая позиционным и непозиционным системам счисления.
Н. Д Угриновича 7 часов изучения темы «Системы счисления», включая 2 проверочные работы. Этих часов достаточно для изучения такой обширной темы.
Далее представлены примеры теоретического материала учебников по теме «системы счисления».
Рисунок 1.2.1. Содержание учебника Л. Л. Босовой
Рисунок 1.2.2 Содержание учебника авторства Н. Д. Угриновича.
У Л. Л. Босовой представлены практические задания в конце изучения всей темы считаемы счисления, а не после каждого отдельного параграфа Задания в основном состоят из перевода чисел в системах счисления, объяснения позиционных и непозиционных систем счисления.
В учебнике Н. Д Угриновича в конце каждого параграфа присутствуют контрольные вопросы по теме и несколько заданий. Например, после параграфа «Позиционные системы счисления» есть такие вопросы и задания
Так же в конце учебника есть ряд практических работ по важным темам курса. Практическая по системам счисления представлена ниже.
В соответствии с требованиями ФГОС к результатам освоения основной образовательной программы основного общего образования содержание обучения должно быть направлено на достижение учащимися личностных, метапредметных и предметных результатов по информатике. Автором выделены требования к личностным результатам и группа метапредметных результатов, развитие которых обеспечивается использованием учебников и других компонентов учебно-методического комплекта (УМК)
Учебники Л. Л Босовой и Н. Д Угриновича соответствуют требованиям обучения по ФГОС.
Таблица 1. Сравнение УУД, формирующихся в рамках изучения темы «Системы счисления» в школьном курсе информатики.
| УУД | Л. Л Босова | Н. Д Угринович |
| 1 | 2 | 3 |
| Коммуни-кативные | приобретают опыт работы в группе; практическое усвоение морально-этических принципов общения и сотрудничества; аргументировать свою точку зрения; выслушивать собеседника и вести диалог; развивать логическое мышление; признавать возможности существования различных точек зрения и права каждого иметь своё мнение. | умение слушать и вступать в диалог, формулирование и аргументация своего мнения, сотрудничество в выполнении упражнений. |
| Регуля-тивные | целеполагание и планирование своей деятельности. | контроль и оценка своей деятельности в рамках урока |
| Познава-тельные | общеучебные (самостоятельное выделение познавательной цели, поиск и выделение информации), самостоятельное создание способов решения проблем творческого и поискового характера; использовать средства информационных и коммуникационных технологий для решения коммуникативных, познавательных и творческих задач. | Построение речевого высказывания в устной форме, контроль и оценка процесса и результатов деятельности |
| Личнос-тные | ориентирование в системе моральных норм и ценностей, вежливое, доброжелательное общение друг с другом, взаимопомощь, ответственность не только за свои успехи, но и за успехи одноклассников. | формирование навыков самоорганизации, контроль и оценка процесса и результатов деятельности |