Файл: Курсовая работа особенности изучения систем счисления в школьном курсе информатики.docx
Добавлен: 06.11.2023
Просмотров: 531
Скачиваний: 19
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Теоретические основы изучения систем счисления в школьном курсе информатики
Анализ темы: «Системы счисления» в школьном курсе информатики
Методические аспекты изучения системы счисления в школьном курсе информатики
2.1 Разработка контрольно-измерительных материалов по теме «Системы счисления»
2.2 Методические рекомендации изучения систем счисления в школьном курсе информатики
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ
ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ М.Е. ЕВСЕВЬЕВА»
Факультет физико-математический
Кафедра физики, информационных технологий и методик обучения
КУРСОВАЯ РАБОТА
ОСОБЕННОСТИ ИЗУЧЕНИЯ СИСТЕМ СЧИСЛЕНИЯ
В ШКОЛЬНОМ КУРСЕ ИНФОРМАТИКИ
Автор работы _____________________________________ К.С. Соболев
Направления подготовки 44.03.05 Педагогическое образование
Профиль Физика. Информатика
Руководитель работы _______________________________ С.И. Проценко
Доцент, кандидат педагогических наук
кафедра физики, информационных технологий и методик обучения
Оценка _________
Саранск 2023
Содержание
Введение 3
1.Теоретические основы изучения систем счисления в школьном курсе информатики 6
1.1Системы счисления, операции над числами в позиционных системах счисления 6
1.2Анализ темы: «Системы счисления» в школьном курсе информатики 12
2.Методические аспекты изучения системы счисления в школьном курсе информатики 20
2.1 Разработка контрольно-измерительных материалов по теме «Системы счисления» 20
2.2 Методические рекомендации изучения систем счисления в школьном курсе информатики 22
Заключение 25
Список используемых источников 26
Приложение А. Технологическая карту урока 29
Введение
Быстрый социальный и научно-технический прогресс требует совершенствования всех звеньев образования. Эффективность новых дорогостоящих средств обучения, таких как компьютер, телевидение, видеотехника, аудиоаппаратура полностью зависит от целей, задач обучения и используемых методов и приемов.
Решая вопрос чему учить, всегда приходится решать вопрос о том, какие компоненты необходимо включить в содержание образования, в какой последовательности их расположить для наилучшего достижения конечной цели – сформировать личность человека в соответствии с социально значимым для своего времени образцом.
Данная тема является актуальной на сегодняшний день. Так как сегодня все больше и больше появляется много новых информационных технологий, это вносит новый элемент в содержание образования, школьного образования в частности. Знание основ информатики и вычислительной техники, умение использовать ЭВМ становятся необходимым каждому человеку, т.е. общеобразовательными.
Необходимость изучения «Системы счисления» в курсе информатики связана с тем, что числа в памяти компьютера представлены в двоичной системе счисления, а для внешнего представления содержимого памяти используют шестнадцатеричную или восьмеричную систему. Данная тема вносит вклад также и в фундаментальное математическое образование школьников.
Уже ни для кого не секрет, что любая ЭВМ предназначена для обработки, преобразования и хранения данных. Для выполнения этих функции ЭВМ должна обладать некоторым способом представления данных. Представление данных заключается в их преобразовании в вид, удобный для последующей обработки либо пользователем, либо ЭВМ.
Форма представления данных определяется их конечным предназначением. В зависимости от этого данные имеют внутреннее и внешнее представление.
Все эти данные для ввода в компьютер должны быть некоторым универсальным образом представлены в виде набора целых чисел, т.е. преобразованы в формат внутреннего представления ЭВМ.
Важным понятием при представлении данных в компьютерах является понятие система счисления.
Актуальность данного исследования обусловлена тем, что в настоящее время возрастает роль творческой, активной, мыслящей личности педагога. Поэтому важнейшей задачей педагогической науки является совершенствование планирования процесса обучения в целом и повышение эффективности управления познавательной деятельностью учащихся.
Объект исследования: процесс обучения теме «Системы счисления» в информатике.
Предмет исследования: формы и методы обучения переводу систем счисления в школьном курсе информатики.
Цель работы: разработка методических рекомендаций для преподавания раздела «Системы счисления» в школьном курсе информатики.
Задачи:
-
изучить теоретический материал школьного курса информатики; -
провести анализ разделов темы «Системы счисления» в школьном курсе информатики; -
разработать контрольно-измерительные материалы по теме «Системы счисления»; -
разработать урок по теме «Системы счисления».
Методы исследования:
1. теоретический: теоретический анализ литературных источников;
2. математический: расчёт и вычисление.
Теоретическая значимость данной работы заключается в том, что
многие подростки и не только, возможно обратят внимание на моё исследование, и сделают выводы, подтверждая их действиями.
Практическая значимость исследования состоит в том, что оно может быть
использовано будущими педагогами для повышения образовательного уровня, учителем математики и информатики для объяснения тем и проведения занимательных уроков.
- 1 2 3 4 5
Теоретические основы изучения систем счисления в школьном курсе информатики
-
Системы счисления, операции над числами в позиционных системах счисления
Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.
Все системы счисления делятся на две большие группы: позиционные и непозиционные системы счисления. В позиционных системах счисления значение цифры зависит от ее положения в числе, а в непозиционных – не зависит.
Преобразование чисел, представленных в двоичной, восьмеричной и шестнадцатеричной системах счисления, в десятичную выполнить довольно легко. Для этого необходимо записать число в развернутой форме и вычислить его значение.
Рассмотрим перевод числа из двоичной системы в десятичную.
Возьмем любое двоичное число, например, 10, 112. Запишем его в развернутой форме и произведем вычисления:
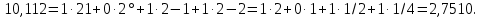
Рассмотрим перевод числа из восьмеричной системы в десятичную.
Возьмем любое восьмеричное число, например, 67 ,58. Запишем его в развернутой форме и произведем вычисления:
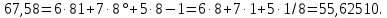
Рассмотрим перевод числа из шестнадцатеричной системы в десятичную.
Возьмем любое шестнадцатеричное число, например, 19F16. Запишем его в развернутой форме (при этом необходимо помнить, что шестнадцатеричная цифра F соответствует десятичному числу 15) и произведем вычисления:
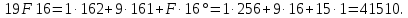
Перевод чисел из десятичной системы в двоичную, восьмеричную и шестнадцатеричную более сложен и может осуществляться различными способами. Рассмотрим один из алгоритмов перевода на примере перевода чисел из десятичной системы в двоичную. При этом необходимо учитывать, что алгоритмы перевода целых чисел и правильных дробей будут различаться.
Алгоритм перевода целых десятичных чисел в двоичную систему счисления. Пусть Адд – целое десятичное число. Запишем его в виде суммы степеней основания 2 с двоичными коэффициентами. В его записи в развернутой форме будут отсутствовать отрицательные степени основания (числа 2):
Aдд =
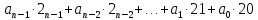
На первом шаге разделим число А на основание двоичной системы, то есть на 2. Частное от деления будет равно
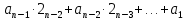
На втором шаге целое частное опять разделим на 2, остаток от деления будет теперь равен
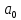
Если продолжать этот процесс деления, то после n-го шага получим последовательность остатков:
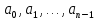
Легко заметить, что их последовательность совпадает с обратной последовательностью цифр целого двоичного числа, записанного в свернутой форме:
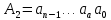
Таким образом, достаточно записать остатки в обратной последовательности, чтобы получить искомое двоичное число.
Алгоритм перевода целого десятичного числа в двоичное будет следующим:
Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание системы (на 2) до тех пор, пока не получится частное, меньшее делителя, то есть меньшее 2.
Записать полученные остатки в обратной последовательности.
В качестве примера рассмотрим перевод десятичного числа 19 в двоичную систему, записывая результаты в таблицу:
В результате получаем двоичное число:
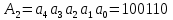
Алгоритм перевода правильных десятичных дробей в двоичную систему счисления. Пусть А – правильная десятичная дробь. В ее записи в развернутой форме будут отсутствовать положительные степени основания (числа 2):
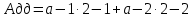
На первом шаге умножим число Адд на основание двоичной системы, то есть на 2. Произведение будет равно: