Программа среднего профессионального образования 44.02.03 Педагогика дополнительного образования (в области физкультурно-оздоровительной деятельности)Дисциплина: Математика.Практическое занятие 6 Выполнил:Обучающийся Абсалямова Суваде РешатовнаПреподаватель:Галкина Людмила СергеевнаТемы: Квадратные и иррациональные уравнения и неравенства. Метод интервалов. Степенная, показательная и логарифмическая функции. Решение тригонометрических уравнений и неравенств. Производная функции. Исследование функции с помощью производной. Неопределенный интеграл. Определенный интеграл. Многогранники и площади их поверхностей. Объем многогранников. Элементы математической статистики. Цель занятия: закрепление навыков решения квадратных, дробно-рациональных и иррациональных уравнений и неравенств, нахождения значений показательных и логарифмических выражений; закрепление навыков решения тригонометрических уравнений и неравенств, а также задач дифференциального исчисления и интегрального исчисления; нахождения площади поверхности и объема многогранника; овладение навыками решения простейших задач математической статистики.Решение примеров подробно прописывается в тетради, заверяется подписью обучающегося. Для проверки в СДО прикрепляется или скан решений, или фото решений (размещенные либо в архиве, либо в текстовом документе, в порядке следования заданий)Задание 1. (Максимальное количество баллов – 1 балл) Решите предложенные уравнения, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты):

---

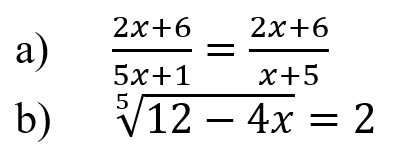
А) Это уравнение можно решить, используя равенство рациональной дроби нулю:

1. 
   Перенесём всё левую часть уравнения.
   

2. 
   Найдем общий знаменатель:
   

(5x+1)*(x+5)

3. 
   Умножим обе части уравнения на общий знаменатель и подведём под одну дробь:
   

4. 
   Составим систему уравнений и решим её:
   

5. 
   Решим первое уравнение. Вынесем общий множитель (2х+6) за скобку:
   

(2х+6)(х+5)-(5х+1)=0Раскроем внутренние скобки:(2х+6)(х+5-5х-1)=0Сократим необходимое:(2х+6)(4-4х)=0Вынесем за скобку общие множители из каждой скобки:2*(х+3)*4(1-х)=0Уравнение равно нулю, если обе части уравнения или одна из них равно нулю:Х+3=0 или 1-х=0Х₁=-3 х₂=1

6. 
   Решим второе неравенство.
   

(х+5)(5х+1) 0Найденные значения х₁, х₂ – корни уравнения, не обращают дробь в ноль.Ответ: -3;1.Б) Решим уравнение, используя формулу. Возведём во вторую степень обе части уравнения:Возведём снова во вторую степень:12-4х=16. Решим полученное уравнение.-4х=16-12-4х=4Х=-1Подставим в исходное уравнение:2=2 - верноОтвет: -1.Задание 2. (Максимальное количество баллов – 1 балл)

---

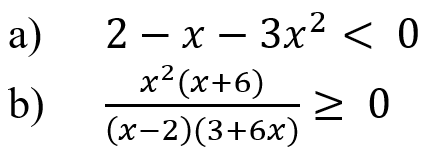
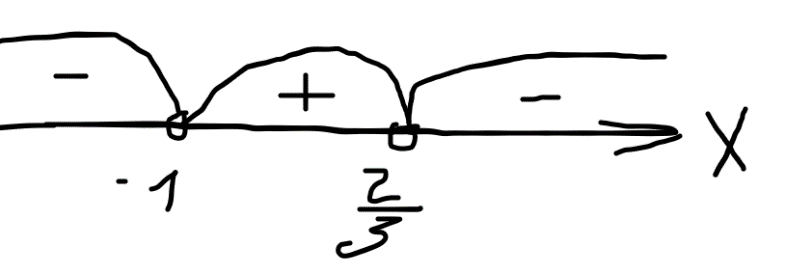
 Решите предложенные неравенства методом интервалов, подробно описывая ход решения: А) 2-х-3х²<0Найдем корни многочлена. Для этого приравняем левую часть неравенства к нулю.2-х-3х²=0А=-3, b= -1, c=2D=b²-4ac=(-1)²-4*(-3)*2=1+24=25Отметим найденные корни на числовой оси и нарисуем интервалыОпределим знак («+» или «-») на одном интервале. Например, при х=0 (это средний интервал). Подставим х=0 в левую часть неравенства:2-0-3*0=2>0 – положительное число, значит на среднем интервале будет стоять знак «+». На остальных интервалах знаки будут чередоваться.Осталось записать интервалы с «-». Так как в неравенстве стоит <0. Таких два интервала. Ответ: (-∞;1) ( ;+∞)Б) Приравняем левую часть неравенства к нулю.Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нолю (т.к. на нуль делить нельзя). Составим систему уравнений и решим её.Решим первое уравнение. 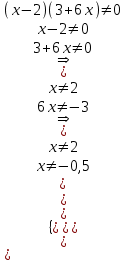Уравнение произведения равно нулю, если один из множителей многочлена равен нулю.Х(х+6)=0Х²=0 или х+6=0Х₁=0 х₂=-6 Решим второе неравенство.Отметим найденные числа на числовом промежутке и нарисуем интервалы

---

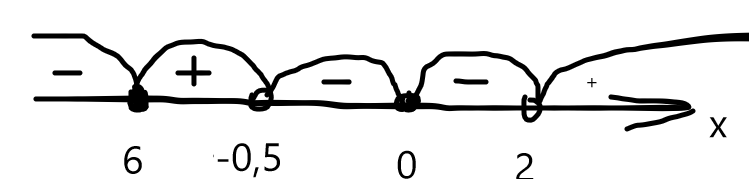
Закрасим кружочки, где значение дроби обращается в нуль. Подставим значения для определения знаков постоянства на промежутке.При х=-7: Значит самый левый промежуток будет иметь знак «-».Подставим значение х=1 , значит четвертый интервал будет иметь знак «-».Подставим значение х=-1 , значит второй интервал будет иметь знак «+».Подставим значение х=-0,2 , значит третий интервал будет иметь знак «-».Подставим значение х=3. , значит пятый интервал будет иметь знак «+».Осталось записать интервалы с «+». Ответ: ∞)Задание 3. 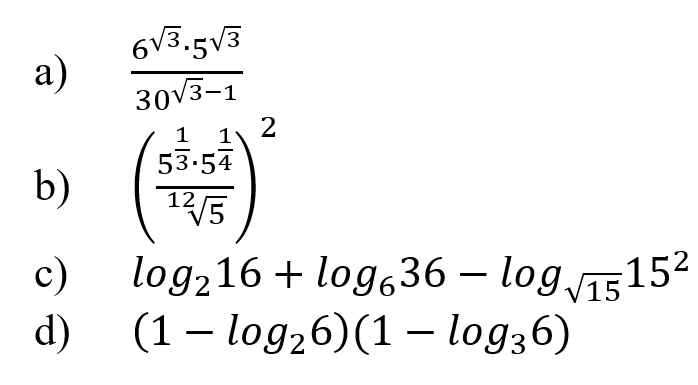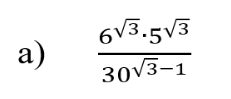(Максимальное количество баллов – 2 балла)Найдите значение выражений, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты): Решение:В знаменателе разложим на множители согласно правилу действий со степенямиВычислим значения степени с одинаковым основанием. Для этого вычтем из степени числителя степень знаменателя, по правилу деления степенных чисел с одним основанием^n-mЗапишем промежуточные расчеты.

---

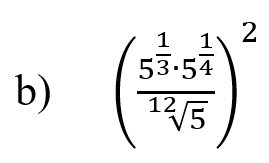
Представим в виде значения со степенью В числителе сложим показатели степени по правилу умножения степенных чисел с одним основанием: Для этого приведем их к общему знаменателю.Далее из показателя степени числителя вычтем показатель степени знаменателя (по правилу деления показателя степени чисел с одинаковым основанием):²Сократим показатель степени и представим в виде числа с корнем.Ответ: 5.По определению логарифма:Подставим полученные значения в выражение, Таким образом 4+2-4=2.Ответ:2.Воспользуемся формулой log_aa=1 и представим число 1 в виде логарифма:Воспользуемся формулой: .Для этого разделим два подлогарифмических выражения с одним основанием и в результате представим подлогарифмические выражении в виде числа, равному основанию, со степенью:Воспользуемся формулой: .Для этого показатель степени подлогарифмического выражения вынесем впреди логарифма

---

Смотрите также файлы

• 4. Общие проблемы малой группы. Динамические процессы в малой группе. Развитие малой группы. Решение практических задач (кейсов).docx

• Формирование интереса к будущей профессиональной деятельности у студентов вуза физической культуры.docx

• Словарь мифологизмов.docx

• Технологические потери электрической энергии в распределительных и питающих сетях.docx

• Ознакомительная лекция, включая инструктаж по соблюдению правил противопожарной безопасности, правил охраны труда, техники безопасности, санитарноэпидемиологических правил и гигиенических нормативов.docx