Используем формулу половинного аргумента:









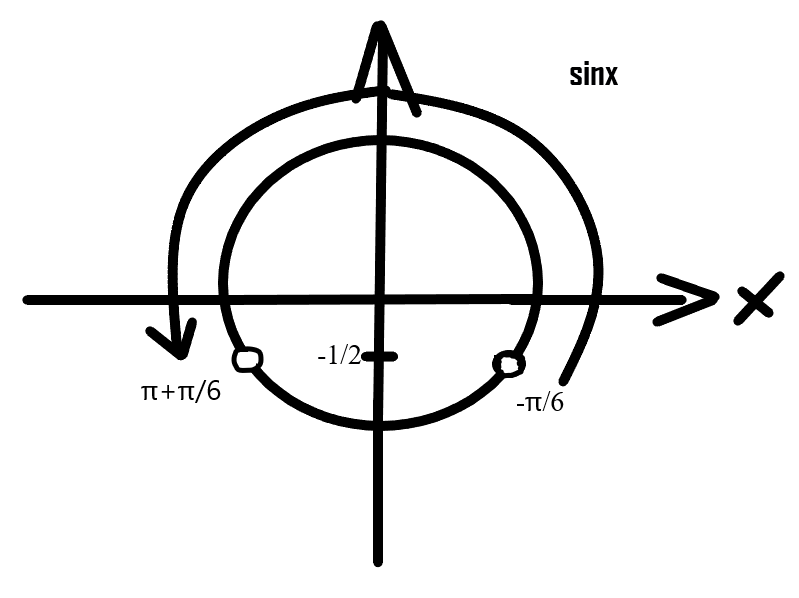
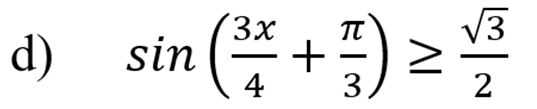
Чтобы решить это неравенство – надо сначала решить соответствующее уравнение:

-это простейшее тригонометрическое уравнение, которое преобразуется в:



Перенесём в правую часть уравнения с противоположным знаком:



Разделим обе части уравнения на :



Данные точки являются точками смены знака неравенства в решениях.





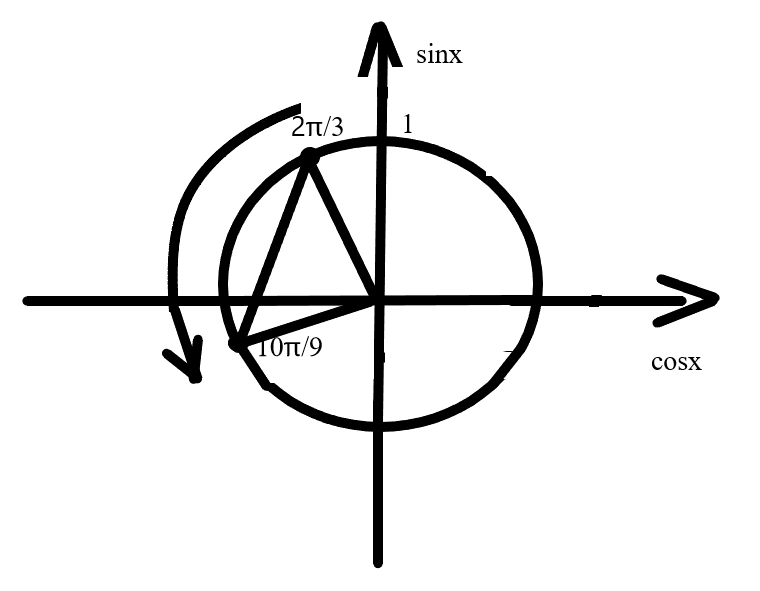
Задание 7. (Максимальное количество баллов – 2 балла)

 Вычислите предложенные производные функций, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты):



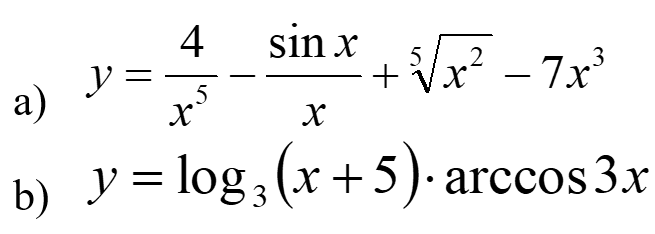
Решение:



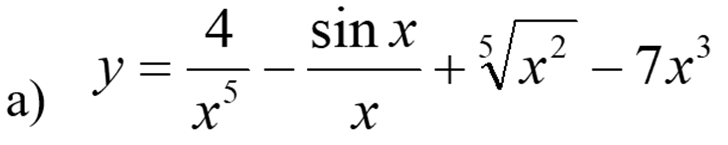
Представим производную в виде суммы производных:

---

Производную этого выражения находим по формуле: (xⁿ)' = n*x^n-1



x^′=1

(-7·x³) ^′=-7·3·x^3-1·x^′=-21·x²

x^′=1





При вычислении были использованы следующие правила дифференцирования: (x^a)' = ax^a-1
(a)' = 0,



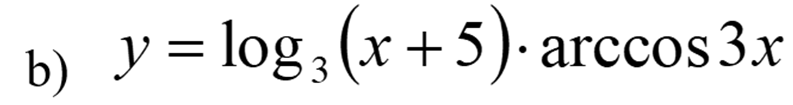
Используем формулу:

Найдем производную первого члена, используя формулу из таблицы производных:



Производная от логарифма и под логарифмического выражения:



Найдем производную второго члена, используя формулы из таблицы производных и свойство сложной функции:



Производная от тригонометрической функции и производная с константой:



Результат:

Задание 8. (Максимальное количество баллов - 4 балла)

 Вам предложена функция 

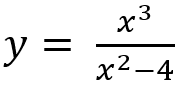
Проведите исследование, согласно схеме:

1.    Найти область определения функции.

2.    Найти точки пересечения с осями.

3.    Исследовать функцию на четность/нечетность.

---

4.    Найти асимптоты.

5.    Найти экстремумы и интервалы монотонности функции.

6.    Найти интервалы выпуклости функции и точки перегиба.

7.    Найти дополнительные точки, уточняющие график.

8.    Построить график.

 Решение:

1. 
   Найти область определения функции.
   

Точки разрыва:



Значит, область определения функции:

∞;-4) (-4;4) (4;+∞)

2. 
   Найти точки пересечения с осями. Приравняем к нулю.
   

Пересечение с осью 0Y: x=0, y=0

Пересечение с осью 0X:

y=0, тогда , х=0

3. 
   Исследовать функцию на четность/нечетность:
   

y(-x) = -y(x), нечетная функция

4. 
   Найти асимптоты:
   

Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:



Находим коэффициент k:





Находим коэффициент b:

---

Получаем уравнение наклонной асимптоты:

y = x
Найдем вертикальные асимптоты. Для этого определим точки разрыва:

x₁ = -2, x₂ = 2
Находим переделы в точке x=-2





x₁ = -2 - точка разрыва II рода и является вертикальной асимптотой.
Находим переделы в точке x=2





x₂ = 2 - точка разрыва II рода и является вертикальной асимптотой.

Найдем наклонную асимптоту при x → -∞:



Находим коэффициент k:





Находим коэффициент b:

---

Получаем уравнение наклонной асимптоты:

y = x

5. 
   Найти y = x^3/(x^2-4)
   Найдем точки разрыва функции: x₁ = 2, x₂ = -2
   Поскольку f(-x)=-f(x), то функция является нечетной. экстремумы и интервалы монотонности функции:
   

1. 4>
   1   2   3

---

Смотрите также файлы

• 4. Общие проблемы малой группы. Динамические процессы в малой группе. Развитие малой группы. Решение практических задач (кейсов).docx

• Формирование интереса к будущей профессиональной деятельности у студентов вуза физической культуры.docx

• Словарь мифологизмов.docx

• Технологические потери электрической энергии в распределительных и питающих сетях.docx

• Ознакомительная лекция, включая инструктаж по соблюдению правил противопожарной безопасности, правил охраны труда, техники безопасности, санитарноэпидемиологических правил и гигиенических нормативов.docx