Файл: Программа среднего профессионального образования 44. 02. 03 Педагогика дополнительного образования (в области физкультурнооздоровительной деятельности) Дисциплина Математика. Практическое занятие 6.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 114
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, как множитель:

Воспользуемся формулой логарифма с новым основанием для первого логарифма и впоследствии сократим:

Ответ:1.
Задание 4. (Максимальное количество баллов – 2 балла)
Решите предложенные уравнения, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты):
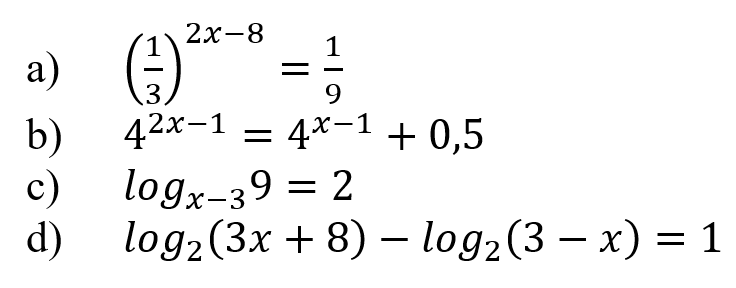
Решение:
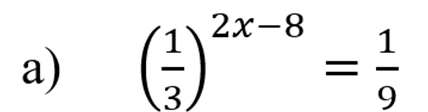
Представим вторую часть уравнения в виде числа со степенью:

Тогда показатели степени с одним основанием равны:

Сделаем проверку:

Верно
Ответ:5.
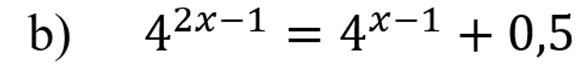
Разложим показательные числа на множители:

Перенесём в левую часть уравнения все числа и переменные:

Сделаем замену. Пусть 4x=t

Получаем квадратное уравнение:

Домножим уравнение на 4:


Разложим квадратное уравнение на множители, для этого(–t) представим в виде (-2t+t):

t-2=0 или t+1=0
t=2 t=-1
Сделаем обратную замену:

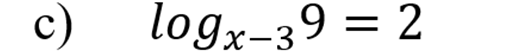
Представим пол логарифмическое выражение в виде показательного числа:

По определению логарифма и по формуле вычислим:

У нас, а=x-3, b=2
Х-3=3, x=3+3, x=6
Сделаем проверку, для этого подставим в исходное уравнение.

2=2-верно.
Ответ: 6.
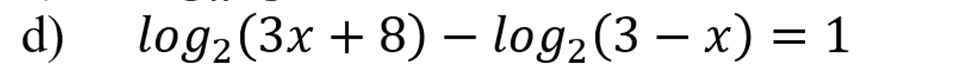
Воспользуемся формулой:

Тогда:

Если, , значит под логарифмическое выражение из уравнения будет равно 2:
, значит под логарифмическое выражение из уравнения будет равно 2:

Перенесём всё в левую часть уравнения:

Приведём к одному знаменателю:

Решим уравнение, как систему уравнений. Так как дробь равна нулю, когда знаменатель не равен нулю, а числитель равен нулю:

Сделаем проверку, для этого подставим в исходное уравнение:

Воспользуемся формулой:


1=1-верно
Ответ: .
.
Задание 5. (Максимальное количество баллов – 2 балла)
Решите предложенные неравенства, подробно описывая ход решения (указывайте формулы и положения, которыми пользуетесь, записывайте промежуточные результаты):
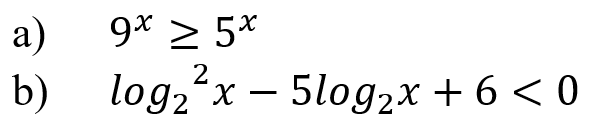
Решение:
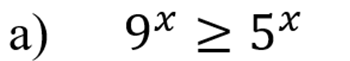
Это показательное уравнение имеет вид:
Запишем неравенство в таком виде:
Логарифмирование:
Теперь возьмём от обоих частей неравенства логарифм по основанию 3. Мы имеем право это делать, так как обе части неравенства больше нуля. Основание логарифма больше единицы, поэтому знак неравенства не изменится.

Разделим на (2- ), предварительно исследовав знак этого выражения, так как 2-
), предварительно исследовав знак этого выражения, так как 2- >0,
>0,  <2
<2
Получим:

Ответ:
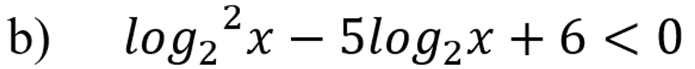
Пусть log2x=t

Разложим (-5t) как (-3t-2t):

Делаем обратную замену:

Ответ: х<4 или ∞)
∞)
Задание 6. (Максимальное количество баллов – 3 балла)
Решите предложенные тригонометрические уравнения и неравенства, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, отобразите графически на единичной окружности соответствующие точки и интервалы):
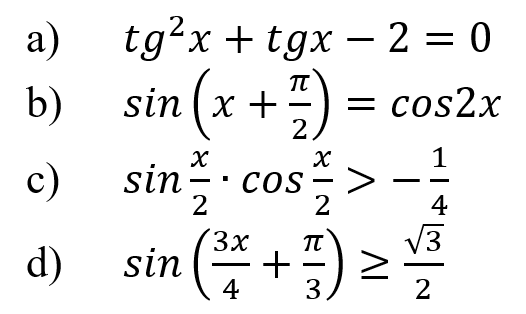
Решение:
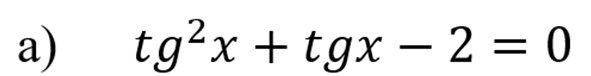
Сделаем замену тригонометрической функции tg(x)=у:

Получаем квадратное уравнение. Решим его, используя дискриминант (a=1,b=1,c=-2)

Делаем обратную подстановку:
π
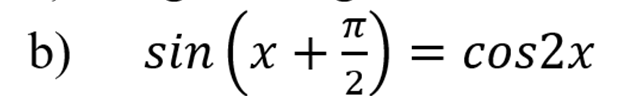
Разложим вторую часть уравнения, согласно тригонометрическому тождеству и формуле двойного угла:

Сделаем замену cosx=t

Делаем обратную замену:
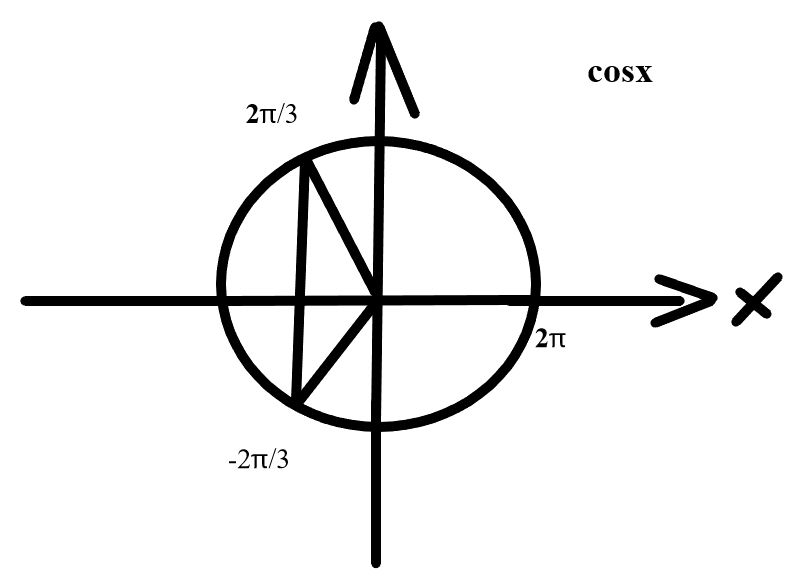
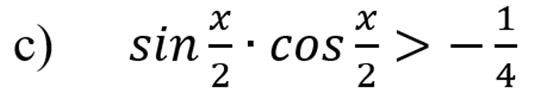
Умножим обе части неравенства на 2:

Воспользуемся формулой логарифма с новым основанием для первого логарифма и впоследствии сократим:
Ответ:1.
Задание 4. (Максимальное количество баллов – 2 балла)
Решите предложенные уравнения, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты):
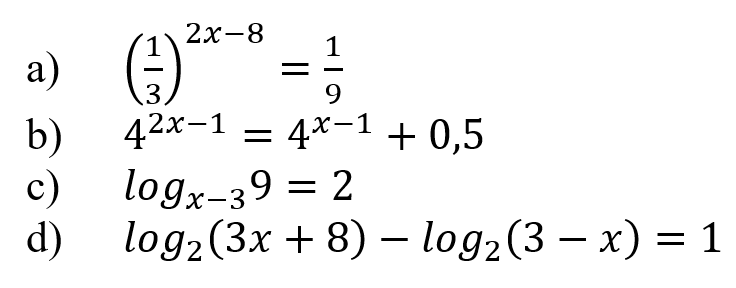
Решение:
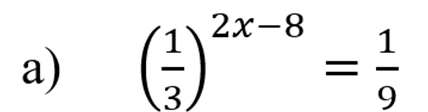
Представим вторую часть уравнения в виде числа со степенью:

Тогда показатели степени с одним основанием равны:

Сделаем проверку:

Верно
Ответ:5.
Разложим показательные числа на множители:
Перенесём в левую часть уравнения все числа и переменные:
Сделаем замену. Пусть 4x=t
Получаем квадратное уравнение:
Домножим уравнение на 4:

Разложим квадратное уравнение на множители, для этого(–t) представим в виде (-2t+t):

t-2=0 или t+1=0
t=2 t=-1
Сделаем обратную замену:

Представим пол логарифмическое выражение в виде показательного числа:
По определению логарифма и по формуле вычислим:
У нас, а=x-3, b=2
Х-3=3, x=3+3, x=6
Сделаем проверку, для этого подставим в исходное уравнение.
2=2-верно.
Ответ: 6.
Воспользуемся формулой:
Тогда:
Если,
Перенесём всё в левую часть уравнения:
Приведём к одному знаменателю:

Решим уравнение, как систему уравнений. Так как дробь равна нулю, когда знаменатель не равен нулю, а числитель равен нулю:

Сделаем проверку, для этого подставим в исходное уравнение:

Воспользуемся формулой:

1=1-верно
Ответ:
Задание 5. (Максимальное количество баллов – 2 балла)
Решите предложенные неравенства, подробно описывая ход решения (указывайте формулы и положения, которыми пользуетесь, записывайте промежуточные результаты):
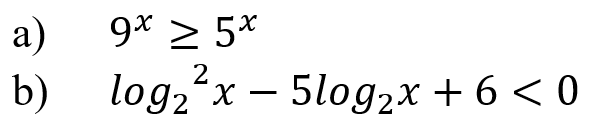
Решение:
Это показательное уравнение имеет вид:
Запишем неравенство в таком виде:
Логарифмирование:
Теперь возьмём от обоих частей неравенства логарифм по основанию 3. Мы имеем право это делать, так как обе части неравенства больше нуля. Основание логарифма больше единицы, поэтому знак неравенства не изменится.

Разделим на (2-
Получим:

Ответ:
Пусть log2x=t
Разложим (-5t) как (-3t-2t):

Делаем обратную замену:

Ответ: х<4 или
Задание 6. (Максимальное количество баллов – 3 балла)
Решите предложенные тригонометрические уравнения и неравенства, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, отобразите графически на единичной окружности соответствующие точки и интервалы):
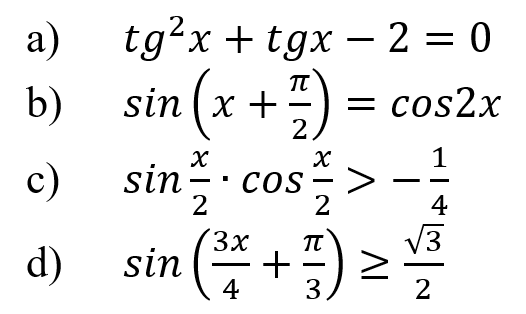
Решение:
Сделаем замену тригонометрической функции tg(x)=у:
Получаем квадратное уравнение. Решим его, используя дискриминант (a=1,b=1,c=-2)

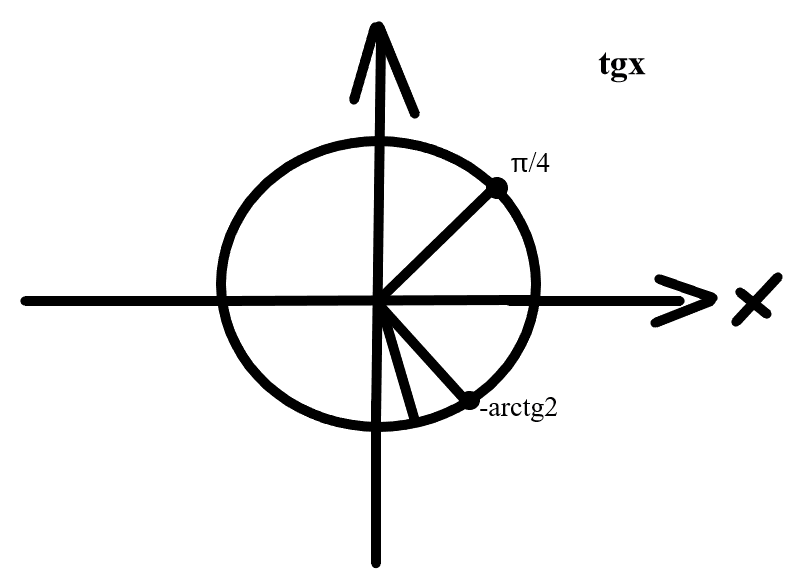
Делаем обратную подстановку:
-
tgx=2 => x1=arctg(-2)+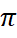
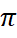 k
k -
tgx=-1=>x2=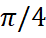
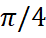 +
+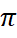
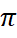 k
k

π
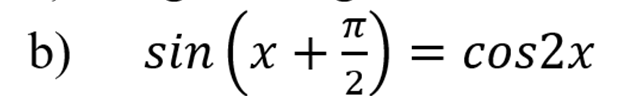
Разложим вторую часть уравнения, согласно тригонометрическому тождеству и формуле двойного угла:

Сделаем замену cosx=t

Делаем обратную замену:
-
cosx=
-


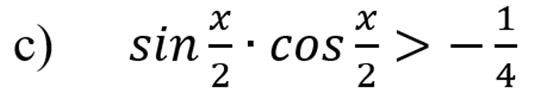
Умножим обе части неравенства на 2: