Файл: Содержание Введение Определение пространственной ориентации объектов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 66
Скачиваний: 2
СОДЕРЖАНИЕ
1. Определение пространственной ориентации объектов
1.1 Параметры пространственной ориентации
1.2 Методы определения пространственной ориентации вектора-базы
2. Разработка и исследование алгоритма
2.1 Общий алгоритм динамического метода решения угловой задачи
2.2 Динамический метод, использующий движение объекта
2.4 Моделирование алгоритма в MathCad
3 Экономическое обоснование работы
3.1 Экономический эффект от внедрения системы ГЛОНАСС
3.2 Определение показателей экономического обоснования проектируемого изделия
3.2.1 Затраты на проектирование и опытное производство проектируемого приемоиндикатора
3.2.2 Себестоимость проектируемой техники в серийном производстве
3.2.3 Годовые эксплуатационные расходы
3.3 Отпускная цена и экономическая эффективность проектируемого блока, имеющего аналог
4. Безопасность жизнедеятельности
Содержание
Введение
1. Определение пространственной ориентации объектов
1.1 Параметры пространственной ориентации
1.2 Методы определения пространственной ориентации вектора-базы
2. Разработка и исследование алгоритма
2.1 Общий алгоритм динамического метода решения угловой задачи
2.2 Динамический метод, использующий движение объекта
2.3 Блок схема алгоритма
2.4 Моделирование алгоритма в MathCad
3 Экономическое обоснование работы
3.1 Экономический эффект от внедрения системы ГЛОНАСС
3.2 Определение показателей экономического обоснования проектируемого изделия
3.2.1 Затраты на проектирование и опытное производство проектируемого приемоиндикатора
3.2.2 Себестоимость проектируемой техники в серийном производстве
3.2.3 Годовые эксплуатационные расходы
3.3 Отпускная цена и экономическая эффективность проектируемого блока, имеющего аналог
4. Безопасность жизнедеятельности
4.1 Безопасность и санитарно-гигиенические условия труда на рабочем месте пользователя ПЭВМ при проведении анализа надежности функционирования бортовой аппаратуры космических аппаратов дистанционного зондирования Земли4.2 Требования к освещению рабочих мест пользователей ПЭВМ. Проектирование и расчет осветительной установки.
Заключение
Список использованной литературы
Приложение
Введение
В настоящее время большой интерес представляет радионавигационная аппаратура ГЛОНАСС и GPS, измеряющая пространственную ориентацию объектов. С развитием новых технологий в области спутниковых радионавигационных систем (СРНС) ГЛОНАСС и GPS навигационные измерения стали доступны практически во всех областях народного хозяйства, вплоть до бытовых приборов.
Применение фазовых методов измерения радионавигационных параметров позволяет расширить функциональные возможности радионавигационной аппаратуры, в частности, измерять пространственную ориентацию объектов.
Спутниковые радионавигационные системы ГЛОНАСС/GPS имеют особенности, которые затрудняют их применение в качестве угломерных систем. Основной проблемой при определении пространственной ориентации объектов является наличие фазовой неоднозначности измерения фазовых сдвигов. При использовании сигналов СРНС отношение длины баз к длине волны сигналов может составлять несколько десятков, поэтому в данном случае проблема разрешения фазовой неоднозначности стоит особенно остро. Методы измерения пространственной ориентации тесно связаны с методами разрешения фазовой неоднозначности, и различные научные школы решают их по-разному. В настоящее время используется три основных направления при решении проблемы измерения пространственной ориентации.
При этом желательно, чтобы алгоритмы разрешения фазовой неоднозначности были одномоментными, т.е. разрешение фазовой неоднозначности должно производиться по результатам измерения параметров сигналов навигационных космических аппаратов (НКА) в любой момент времени. Такими методами являются переборные методы, в которых перебираются все возможные значения фазовых сдвигов сигналов НКА, а решение выбирается по критерию максимального правдоподобия. Однако переборные методы требуют априорных данных о конфигурации антенной платформы, т.е. длину баз и углы между ними. На практике возможны случаи полной априорной неопределенности, например, при установке антенной системы на объекте, когда антенны устанавливаются в произвольных точках, а длина баз достигает нескольких метров.
1. Определение пространственной ориентации объектов
1.1 Параметры пространственной ориентации
Для решения задачи определения пространственной ориентации объектов необходимо осуществлять пересчет направляющих косинусов из одной системы координат в другую. Физические углы заданы в местной топоцентрической системе координат (ТЦСК) углами Эйлера. Координаты навигационных космических аппаратов (НКА) СРНС задаются в декартовой геоцентрической системе координат (ГЦСК), координаты объекта-потребителя определяются в геодезической системе координат.
Геоцентрическая гринвичская система координат жестко связана с Землей. В прямоугольной ГЦСК центр находится в центре Земли
, ось X направлена на Гринвич, ось Z направлена север, ось Y - дополняет систему координат до правой (рис.1.1).
С ГЦСК связан референц-эллипсоид, описывающий форму Земли, относительно которого задаются географические координаты объекта (широта j, долгота l, высота h). ГЦСК и географические координаты связаны выражениями
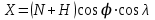 ,
,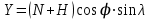 (1.1)
(1.1)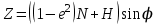 ,
,где X,Y,Z - координаты объекта в ГЦСК, j - широта, l - долгота, H высота,
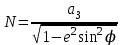 , аЗ - экваториальный радиус Земли, е - эксцентриситет Земли.
, аЗ - экваториальный радиус Земли, е - эксцентриситет Земли.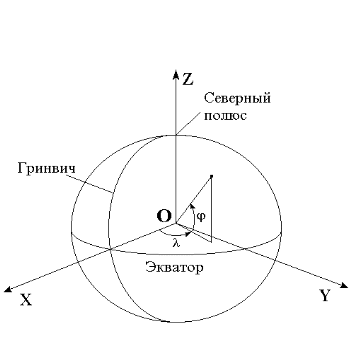
Рис. 1.1. Геоцентрическая система координат
В настоящее время применяются различные ГЦСК. Каждая система включает в себя эллипсоид, описывающий форму Земли. Существуют общеземные системы координат, описывающие Землю в целом, и референцные системы, максимально точно описывающие какой-либо регион . В России распространены референцная система координат 1942 года и общеземная система ПЗ-90 (Параметры Земли 1990 г.). С июля 2002 г. в России официально введена референцная система координат СК-95. В США и других странах широко распространена общеземная система координат WGS-84 . В международной практике принято использовать для перехода между прямоугольными координатами семь параметров Хельмерта, которые определяют сдвиг начала координат Dx,y,z, развороты относительно осей w, j, e и масштабный коэффициент d
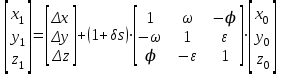 . (1.2)
. (1.2)Такое соотношение справедливо только для почти совпадающих систем координат, так как тригонометрические функции заменены в матрице поворота их приближенными значениями. Кроме того, один масштабный коэффициент предполагает равномерное растяжение-сжатие по всем трем осям, в общем же случае он должен быть заменен метрическим тензором, описывающим неравномерное растяжение.
В вышеприведенных геоцентрических системах координаты объекта могут различаться на десятки и даже сотни метров, однако направления между двумя пунктами различаются на доли угловой секунды, поэтому параметры пространственной ориентации, определенные в одной ГЦСК, будут справедливы и в других ГЦСК.
Связанная с объектом система координат задается следующим образом (рис.1.2): начало координат совпадает с центром масс объекта, ось X направлена вдоль продольной оси объекта, ось Y направлена вверх, ось Z дополняет систему до правой.

Рис. 1.2. К определению связанной системы координат
Аналогичным образом задается топоцентрическая система координат, связана с местоположением объекта. Она представляет из себя прямоугольную систему координат, начало которой совпадает с местоположением объекта, ось Xт направлена на север (по истинному меридиану), ось Yт направлена вертикально вверх, ось Zт дополняет систему до правой системы координат и направлена на восток по горизонтали. Преобразование вектора из ТЦСК в ГЦСК осуществляется следующим линейным преобразованием:
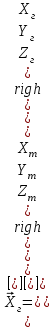 (1.3)
(1.3)где
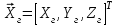 - вектор, заданный в ГЦСК,
- вектор, заданный в ГЦСК, 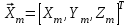 - вектор, заданный в ТЦСК, Cтг - матрица линейного преобразования из ТЦСК в ГЦСК.
- вектор, заданный в ТЦСК, Cтг - матрица линейного преобразования из ТЦСК в ГЦСК.Поскольку Cтг описывает ортогональное преобразование, то обратное преобразование вектора из ГЦСК в ТЦСК можно представить в виде
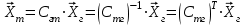 (1.4)
(1.4)При определении углового положения объекта в пространстве чаще всего используют углы Эйлера: угол курса К, (угол рыскания), угол тангажа y (дифферента, килевой качки) и угол крена q (бортовой качки).

Рис.1.3 К определению углов курса и тангажа
Угол курса К (рис.1.3) - это угол между проекцией продольной оси объекта на горизонтальную плоскость (плоскость XOZ) и осью OX (направлением на север) в топоцентрической системе координат. Угол курса отсчитывается от истинного меридиана (ось OXТ) в направлении оси OZТ и может принимать значения от 0 до 360°.
Угол тангажа y - это угол между продольной осью объекта и горизонтальной плоскостью. Значения угла тангажа лежат в пределах ± 90°.
Угол крена q - это угол поворота объекта вокруг продольной оси (рис.1.4). Значения угла крена лежат в пределах ± 180°.

Рис. 1.4. К определению угла крена
Углы К, , q представляют собой углы Эйлера , описывающие угловое положение объекта, совершившего в ТЦСК последовательно поворот вокруг оси ОХт на угол крена q, вокруг оси ОZт на угол тангажа и вокруг оси ОYт на угол курса K из начального положения К = = q = 0.
1.2 Методы определения пространственной ориентации вектора-базы
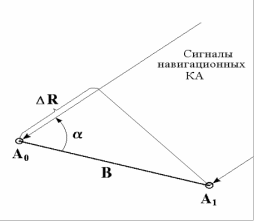
Рис. 1.5 Измерение ориентации вектора базы
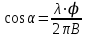 , (1.5)
, (1.5)где
Выражение (1) является уравнением однобазового интерферометра и широко применяется в теории фазовых пеленгаторов и антенных решеток.
Направляющие косинусы вектора-базы могут быть определены из выражения для скалярного произведения векторов:
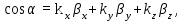 (1.6)
(1.6)где x,y,z - направляющие косинусы вектора-базы,
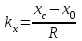 (1.7)
(1.7)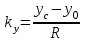 (1.8)
(1.8)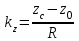 , (1.9)
, (1.9)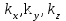 - направляющие косинусы вектора-направления на НКА,
- направляющие косинусы вектора-направления на НКА,xc, yc, zc - координаты НКА,
x0, y0, z0 - координаты объекта,
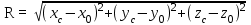 (1.10)
(1.10)- расстояние между объектом и НКА.
Вычисления можно производить в ГЦСК или в ТЦСК.
Для нахождения положения вектора-базы в пространстве требуется измерить фазовые сдвиги сигналов двух НКА.
Следствием нелинейности является зависимость погрешности вычисления ориентации от пространственной ориентации вектора-базы. При уменьшении угла между вектором-базой и направлением на один из НКА погрешность вычисления ориентации вектора-базы резко возрастает.
Для вычисления ориентации вектора-базы при неизвестной длине базы минимальное созвездие состоит из трех НКА, и погрешность вычисления ориентации зависит только от расположения НКА.
пространственный ориентация алгоритм спутниковый
2. Разработка и исследование алгоритма
2.1 Общий алгоритм динамического метода решения угловой задачи
Система уравнений для решения угловой задачи имеет вид (момент времени t0):
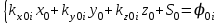 (2.1.1)
(2.1.1)Для момента времени t1