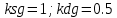Файл: 2. Составление структурной схемы системы и определение передаточной функции, разомкнутой и замкнутой систем между задающим воздействием и выходом сар. Составление соответствующих дифференциальных уравнений и уравнений статики. 3.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 46
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3. Построить область устойчивости в функции параметров элементов САУ указанных преподавателем.
6. Расчет нулей и полюсов системы, степень устойчивости и колебательность системы.
7.Выбор параметров регулятора из условия минимума среднеквадратичного отклонения.
Определим основные показатели переходного процесса:
Время регулирования (время за которое yt достигает нового установившегося значения. Учитывая, что полное затухание в системе происходит лишь при t→∞, длительность переходного процесса ограничивают тем моментом времени, когда регулируемая величина начинает отклоняться от установившегося значения менее чем на 5%:):
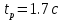
Перерегулирование (равное отношению максимального значения управляемой величины в переходном процессе к установившемуся значению):
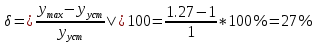
Затухание (характеризующее быстроту затухания колебательного процесса):
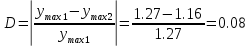
Убедимся в правильности построения области устойчивости. Для этого возьмем точку, которая состоит внутри графика х= 0,5 ksg=1. И построим кривую переходного процесса.
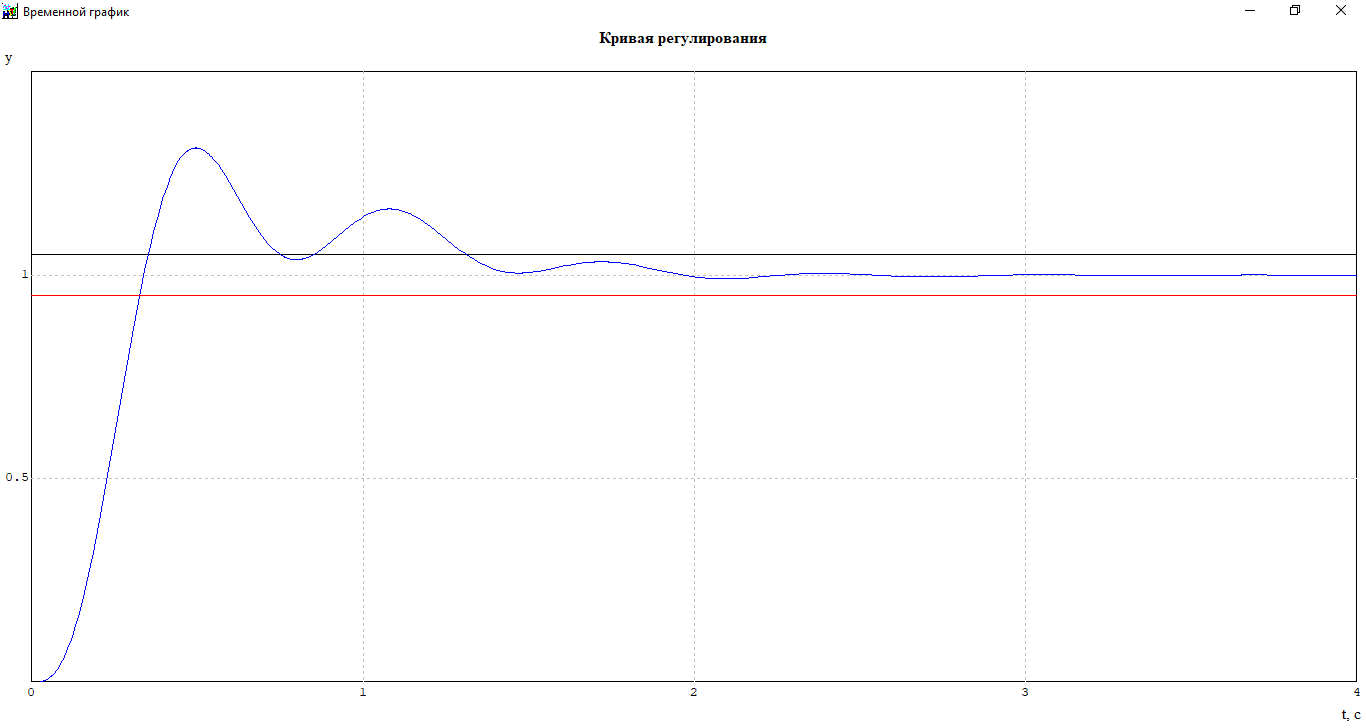
Рисунок 11-Кривая переходного процесса замкнутой системы по задающему воздействию (Макроблок и преобразованная схема.mrj)
Время регулирования: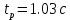
Перерегулирование: 
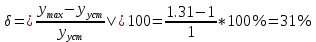
Затухание: 
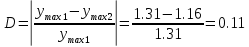
Выберем параметры вне области устойчивости х=1, ksg=3.5
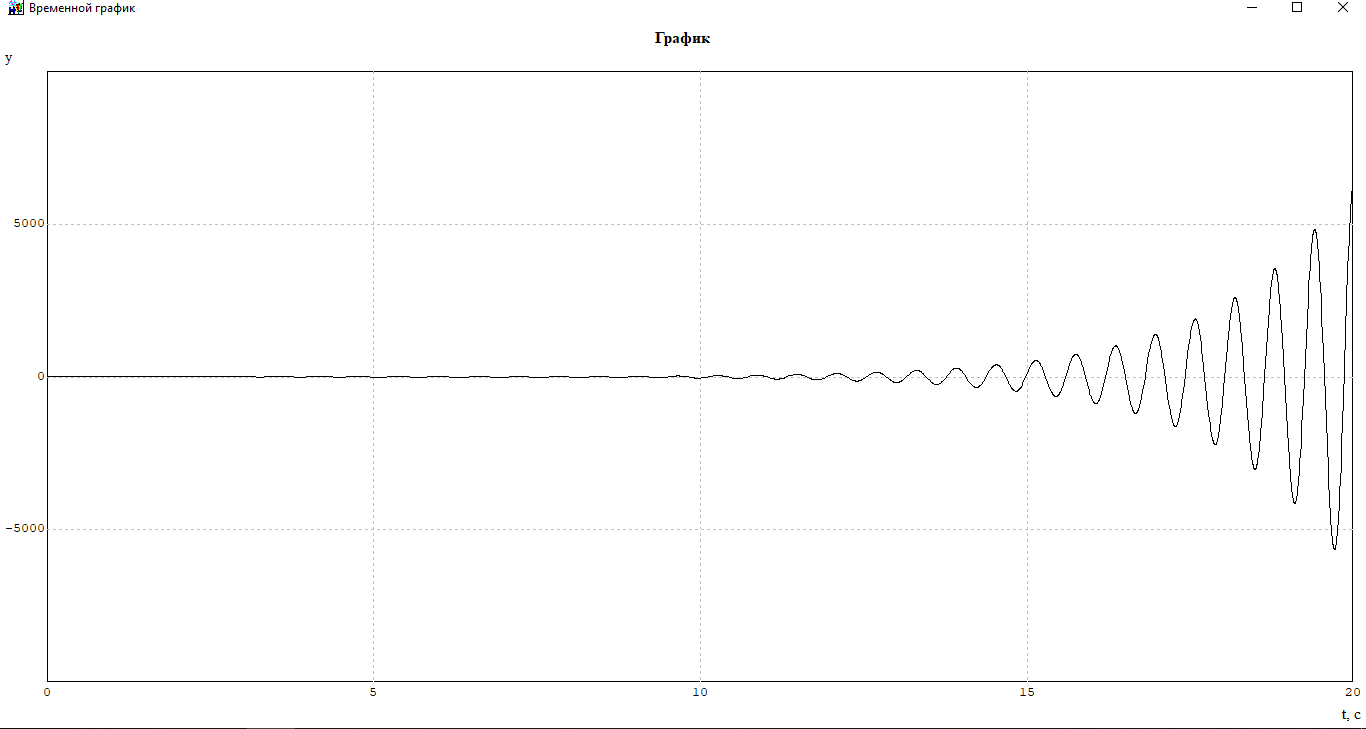
Рисунок 12-Кривая переходного процесса замкнутой системы по задающему воздействию
(Макроблок и преобразованная схема.mrj)
В результате моделирования, мы убедились, что при заданных параметрах система неустойчива.
5. Построение асимптотических ЛАЧХ.
Расчеты проведем с использованием среды Mathcad. (расчет ЛАХ.xmcd)
П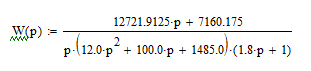
ередаточная функция для построения ЛАЧХ будет иметь вид:
Асимптотические ЛАЧХ можно построить, используя минимум вычислений, непосредственно по виду передаточной функции по следующему алгоритму:
Частота №1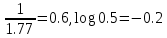
Частота №2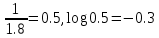
Т.к частоты находятся значительно близко, то будем считать их за одну.
Частота №3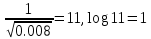
В логарифмической плоскости в логарифмическом масштабе отмечают полученные сопрягающие частоты (частоты, на которых асимптоты, образующие ЛАЧХ меняют наклон) по правилу, записанному выше, отмечают базовую точку С с координатами C (1; 20lg k) , где k - коэффициент усиления в передаточной функции.
Рассчитаем С:
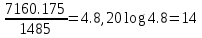
Асимптота в диапазоне от участка левее первой сопрягающей частоты до 1 будет иметь наклон -20 дБ/дек.
(Между частотами №1 и №2 образуется наклон в 0 дБ/дек)
Асимптота в диапазоне от 2 до 3 3 будет иметь наклон -20 дБ/дек. ( 1-ый порядок, знаменатель)
Асимптота в диапазоне от
3 до участка правее сопрягающей частоты 3 будет иметь наклон -40 дБ/дек. ( 2-ый порядок, знаменатель)
Получим готовый ЛАЧХ.
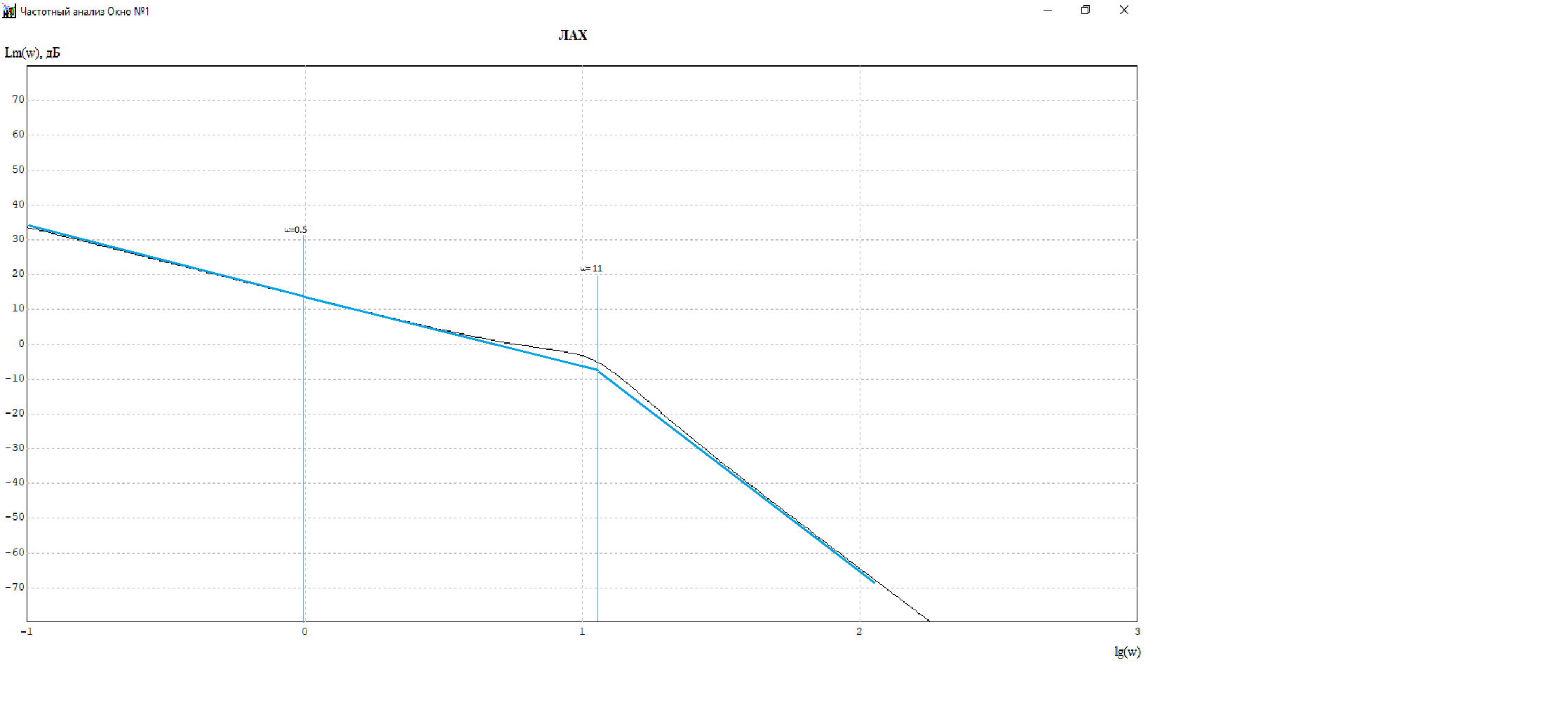Рисунок 13- Асимптотические ЛАЧХ(ЛАЧХ.png)
Черная линия на рисунке построена с помощью программы «Paint»
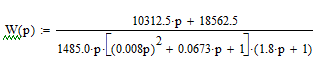
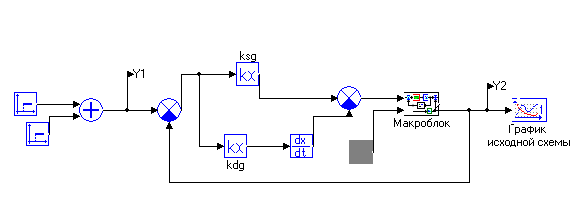
Рисунок 14-Схема для расчета (Расчет нулей и полюсов.mrj)
Полюсами системы называют корни уравнения знаменателя.
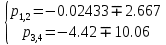
Нулями системы-корни уравнения числителя. В рассматриваемом случае нули отсутствуют.
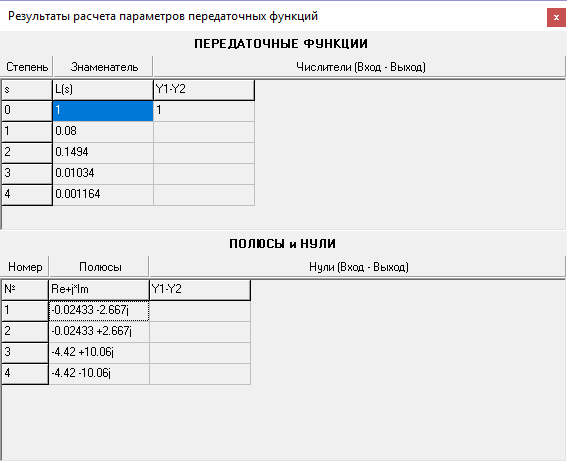
Рисунок 15- Результаты расчета
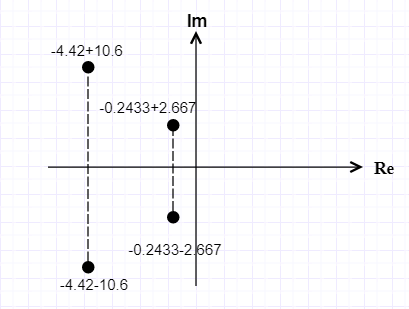
Рисунок 16- Схема расчета корней
Рассчитаем степень устойчивости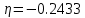
- расстояние до мнимой ближайшего к ней коня характеристического уравнения.
Колебательность системы:
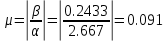, где 
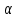- действительная часть ближайшего корня, 
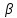- мнимая.
Собираем следующую схему:
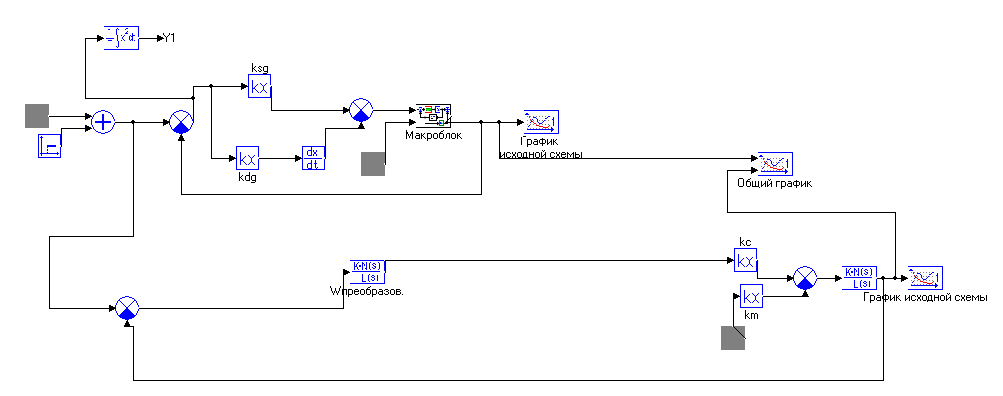
Рисунок 17 - Структурная схема (Расчет ошибок.mrj)
З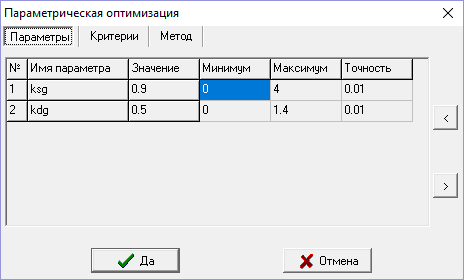
адаем параметры оптимизации:
Результаты оптимизации:
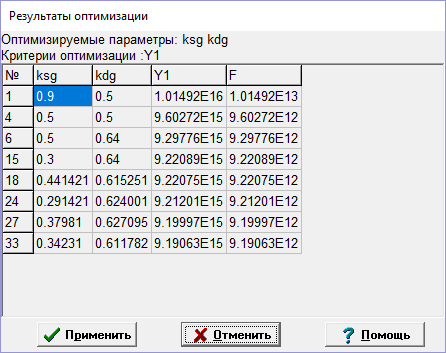
В результате оптимизации получаем следующие значения ksg и kdg при которых среднеквадратическая ошибка минимальна: ksg=0.34; kdg=0.61
Кривая переходного процесса по задающему воздействию при оптимизированных значениях:
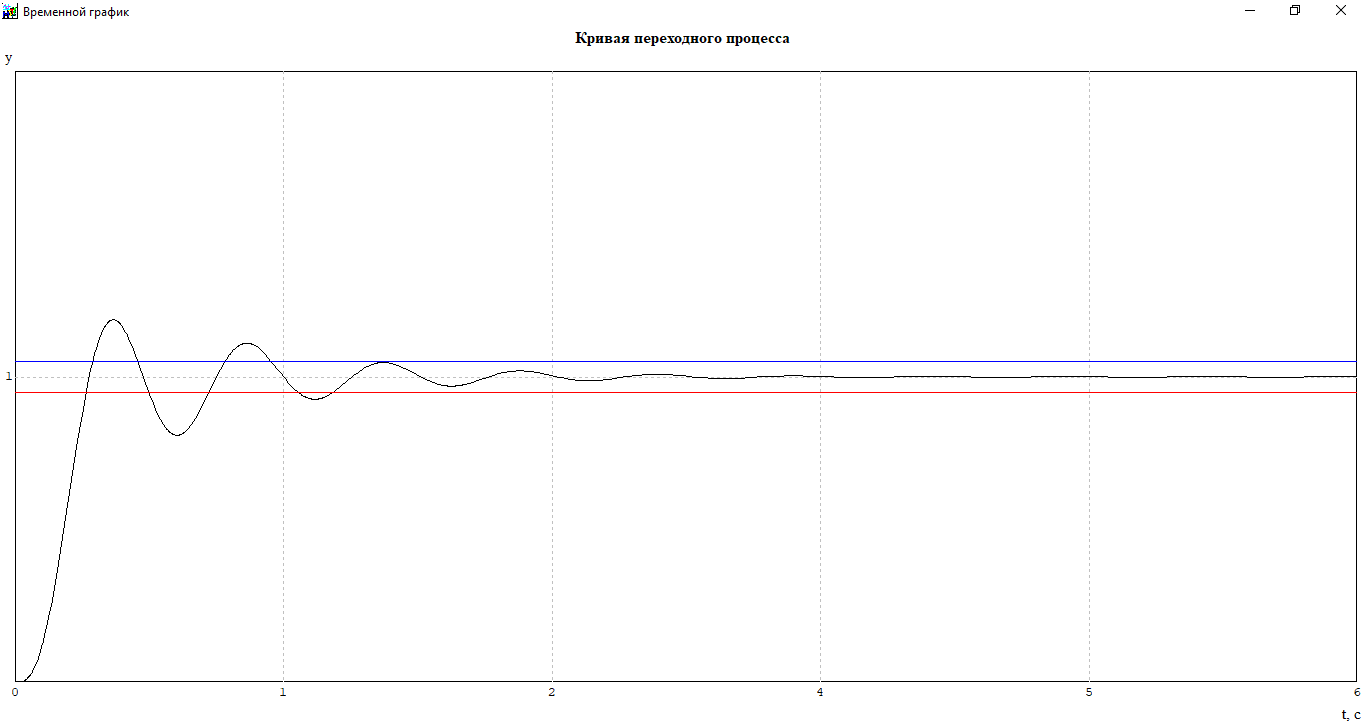
Рисунок 18- Кривая переходного процесса по задающему воздействию после оптимизации(Макроблок и преобразованная схема.mrj)
Время регулирования: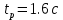
Перерегулирование:
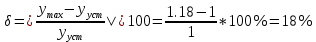
Затухание: 
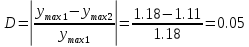
Выберем значения из области устойчивости ksg=2.5; kdg=0.65
Кривая переходного процесса по задающему воздействию при оптимизированных значениях:
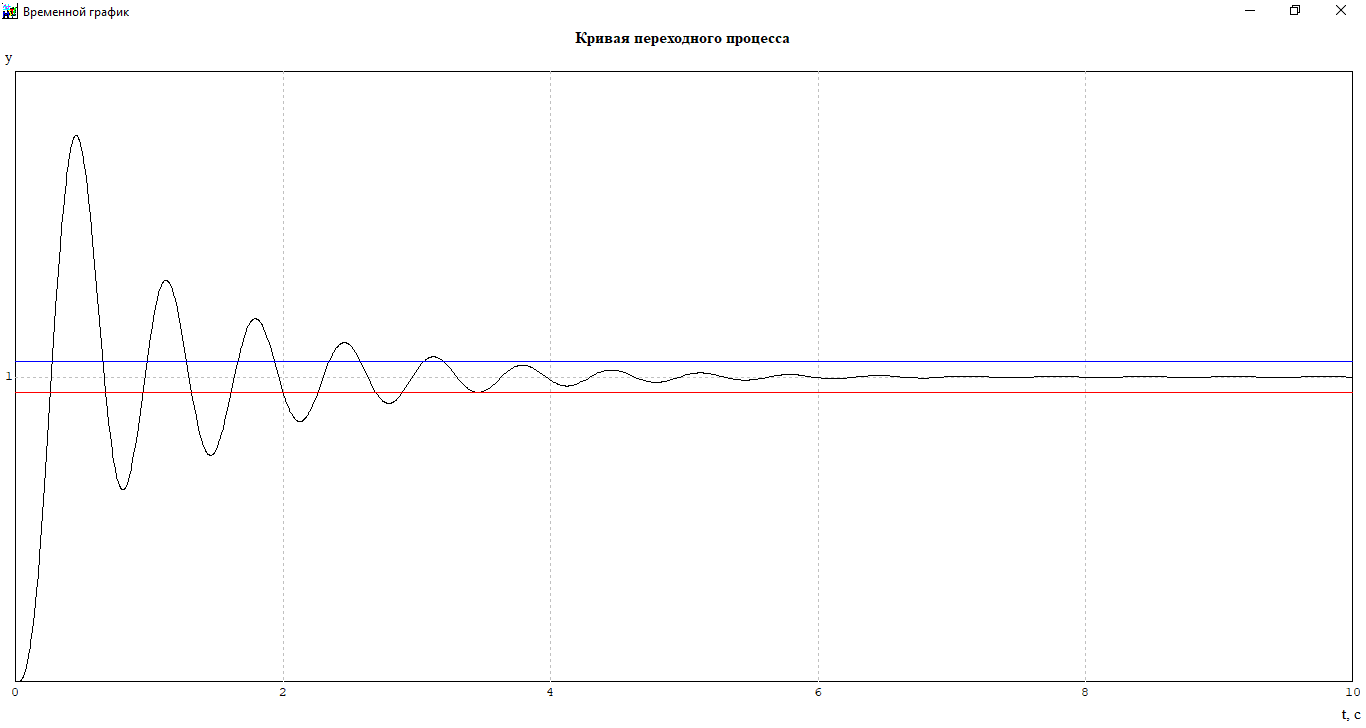
Рисунок 19- Кривая переходного процесса по задающему воздействию после оптимизации
Время регулирования: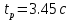
Перерегулирование: 
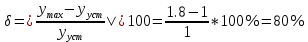
Затухание: 
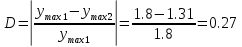
Рисунок 20 - Структурная схема (Расчет ошибок .mrj)
Расчеты проведем с использованием среды Mathcad. (расчет ошибки.xmcd)
Рассчитаем коэффициенты ошибок для исходных данных.
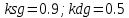
Передаточная функция замкнутой системы по задающему воздействию:
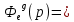
Найдем коэффициент позиционной шибки (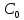
- показывает степень влияния на величину ошибки величины входного сигнала)
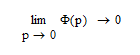
Далее коэффициент скоростной ошибки (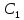
-показывает степень влияния ошибки скорости изменения входного сигнала)
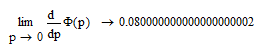
И коэффициент ошибки по ускорению (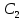
- показывает степень влияния на величину ошибки ускорения входного сигнала)
П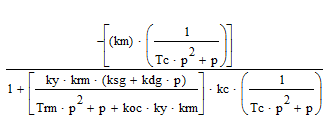
ередаточная функция замкнутой системы по возмущающемуся воздействию:
=
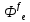Найдем коэффициент позиционной ошибки (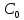 - показывает степень влияния на величину ошибки величины входного сигнала)
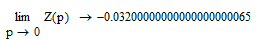
Далее коэффициент скоростной ошибки (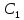 -показывает степень влияния ошибки скорости изменения входного сигнала)
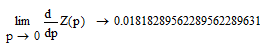
И коэффициент ошибки по ускорению ( - показывает степень влияния на величину ошибки ускорения входного сигнала)
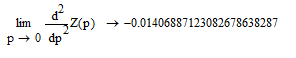
Рассчитаем коэффициенты ошибок для начального приближения(область устойчивости).
Время регулирования (время за которое yt достигает нового установившегося значения. Учитывая, что полное затухание в системе происходит лишь при t→∞, длительность переходного процесса ограничивают тем моментом времени, когда регулируемая величина начинает отклоняться от установившегося значения менее чем на 5%:):
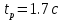
Перерегулирование (равное отношению максимального значения управляемой величины в переходном процессе к установившемуся значению):
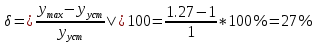
Затухание (характеризующее быстроту затухания колебательного процесса):
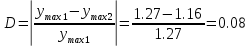
Убедимся в правильности построения области устойчивости. Для этого возьмем точку, которая состоит внутри графика х= 0,5 ksg=1. И построим кривую переходного процесса.
Рисунок 11-Кривая переходного процесса замкнутой системы по задающему воздействию (Макроблок и преобразованная схема.mrj)
Время регулирования:
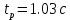
Перерегулирование:
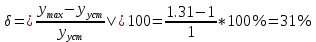
Затухание:
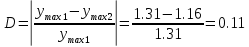
Выберем параметры вне области устойчивости х=1, ksg=3.5
Рисунок 12-Кривая переходного процесса замкнутой системы по задающему воздействию
(Макроблок и преобразованная схема.mrj)
В результате моделирования, мы убедились, что при заданных параметрах система неустойчива.
5. Построение асимптотических ЛАЧХ.
Расчеты проведем с использованием среды Mathcad. (расчет ЛАХ.xmcd)
П
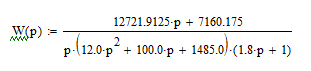ередаточная функция для построения ЛАЧХ будет иметь вид:Асимптотические ЛАЧХ можно построить, используя минимум вычислений, непосредственно по виду передаточной функции по следующему алгоритму:
-
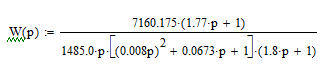Передаточную функцию объекта управления или системы преобразуют к следующему стандартному виду (свободный член у всех множителей равен 1)
-
Из полученного выражения определяют сопрягающие частоты (частоты, на которых будет происходить изменение наклона ЛАЧХ), условно нумеруя их в порядке возрастания:
Частота №1
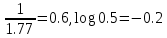
Частота №2
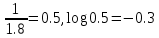
Т.к частоты находятся значительно близко, то будем считать их за одну.
Частота №3
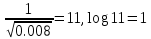
В логарифмической плоскости в логарифмическом масштабе отмечают полученные сопрягающие частоты (частоты, на которых асимптоты, образующие ЛАЧХ меняют наклон) по правилу, записанному выше, отмечают базовую точку С с координатами C (1; 20lg k) , где k - коэффициент усиления в передаточной функции.
Рассчитаем С:
-
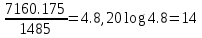
Построение ЛАЧХ начинается с низкочастотного участка, т.е. участка левее первой сопрягающей частоты 1 . Для этого через точку С проводится прямая под наклоном r 20 дБ/дек, где r – показатель степени при p в исходном выражении для передаточной функции . Часть полученной прямой левее первой сопрягающей частоты 1 и дает искомый низкочастотный участок. -
Далее строят вторую асимптоту, которая начинается из конца первой и располагается в диапазоне от 1 до 2 . Наклон второй асимптоты изменяют по отношению к наклону первой на 20 дБ/дек или 40 дБ/дек в зависимости от порядка и местонахождения звена, для которого получена частота 1 .
Асимптота в диапазоне от участка левее первой сопрягающей частоты до 1 будет иметь наклон -20 дБ/дек.
(Между частотами №1 и №2 образуется наклон в 0 дБ/дек)
Асимптота в диапазоне от 2 до 3 3 будет иметь наклон -20 дБ/дек. ( 1-ый порядок, знаменатель)
Асимптота в диапазоне от
3 до участка правее сопрягающей частоты 3 будет иметь наклон -40 дБ/дек. ( 2-ый порядок, знаменатель)
Получим готовый ЛАЧХ.
Рисунок 13- Асимптотические ЛАЧХ(ЛАЧХ.png)Черная линия на рисунке построена с помощью программы «Paint»
6. Расчет нулей и полюсов системы, степень устойчивости и колебательность системы.
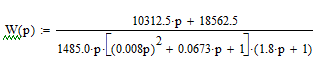
Рисунок 14-Схема для расчета (Расчет нулей и полюсов.mrj)
Полюсами системы называют корни уравнения знаменателя.
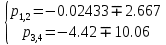
Нулями системы-корни уравнения числителя. В рассматриваемом случае нули отсутствуют.
Рисунок 15- Результаты расчета
Рисунок 16- Схема расчета корней
Рассчитаем степень устойчивости
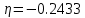- расстояние до мнимой ближайшего к ней коня характеристического уравнения.Колебательность системы:
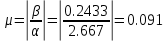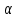, где - действительная часть ближайшего корня, 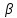- мнимая.7.Выбор параметров регулятора из условия минимума среднеквадратичного отклонения.
Собираем следующую схему:
Рисунок 17 - Структурная схема (Расчет ошибок.mrj)
З
адаем параметры оптимизации:
Результаты оптимизации:
В результате оптимизации получаем следующие значения ksg и kdg при которых среднеквадратическая ошибка минимальна: ksg=0.34; kdg=0.61
Кривая переходного процесса по задающему воздействию при оптимизированных значениях:
Рисунок 18- Кривая переходного процесса по задающему воздействию после оптимизации(Макроблок и преобразованная схема.mrj)
Время регулирования:
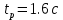
Перерегулирование:
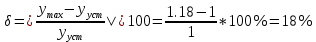
Затухание:
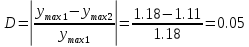
8.Повторить результаты пункта 4
Выберем значения из области устойчивости ksg=2.5; kdg=0.65
Кривая переходного процесса по задающему воздействию при оптимизированных значениях:
Рисунок 19- Кривая переходного процесса по задающему воздействию после оптимизации
Время регулирования:
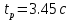
Перерегулирование:
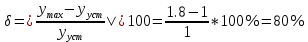
Затухание:
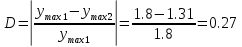
9. Вычисление коэффициентов ошибок по задающему, возмущающемуся воздействиям для параметров регулятора.
Рисунок 20 - Структурная схема (Расчет ошибок .mrj)
Расчеты проведем с использованием среды Mathcad. (расчет ошибки.xmcd)
Рассчитаем коэффициенты ошибок для исходных данных.
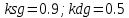
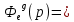
Передаточная функция замкнутой системы по задающему воздействию: Найдем коэффициент позиционной шибки (
- показывает степень влияния на величину ошибки величины входного сигнала) Далее коэффициент скоростной ошибки (
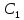-показывает степень влияния ошибки скорости изменения входного сигнала)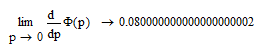 И коэффициент ошибки по ускорению (
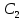- показывает степень влияния на величину ошибки ускорения входного сигнала)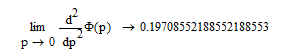 П
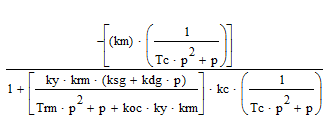ередаточная функция замкнутой системы по возмущающемуся воздействию: 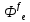= Найдем коэффициент позиционной ошибки (
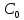- показывает степень влияния на величину ошибки величины входного сигнала)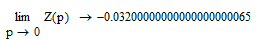 Далее коэффициент скоростной ошибки (
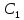-показывает степень влияния ошибки скорости изменения входного сигнала)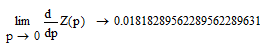 И коэффициент ошибки по ускорению (
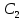- показывает степень влияния на величину ошибки ускорения входного сигнала)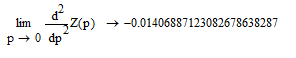 Рассчитаем коэффициенты ошибок для начального приближения(область устойчивости).